基于模型集动态优化的具有有界扰动系统多模型自适应控制
2010-08-24林金星费树岷
林金星 费树岷
(1南京邮电大学自动化学院,南京 210003)
(2东南大学自动化学院,南京 210096)
传统的自适应控制对参数时不变或慢时变的对象能进行很好的控制.但当工况条件改变、故障或外部环境变化等因素导致对象参数发生大的变动时,系统暂态响应会明显变差.多模型自适应控制(MMAC)方法为上述问题的解决提供了一种有效的思路[1].MMAC最初以连续时间线性系统[1-2]为研究对象.近年来,国际上对 MMAC 的研究已拓展到离散时间线性系统[3]、非线性系统[4-5]以及随机系统[6-7],在这期间国内学者又提出了一些改进算法[8-9],但对具有扰动系统的研究并不多见.此外,为提高系统暂态性能,MMAC方法必须建立大量的固定模型以覆盖系统可变参数的变化范围.假设系统有3个可变参数(a1,a2,a3),若对每个参数区间取10个采样值,则共需10×10×10=1 000个固定模型.固定模型数目过多的直接后果是计算负担过重,对硬件设备的要求迅速提高,甚至会限制系统采样周期的减小.文献[10]通过动态调节可移动参数集的中心以覆盖系统的最优估计参数;文献[11]采用Localization技术动态精简系统待选模型集.但这些方法只是对模型的选择作了优化,并没有减少固定模型的数目.文献[12]通过不断缩小模型参数估计区域以及移动模型子集来优化模型集;文献[9]采用分层递阶结构方法设计模型集.但上述方法结构较为复杂,而且没有从根本上降低固定模型的数目.
针对一类具有有界扰动的离散时间时变被控对象,本文提出基于模型集动态优化的多模型自适应控制算法.采用最优可行子集定位、动态覆盖的优化策略动态建立被控对象的固定模型集,在不降低系统控制精度的情况下,降低了固定模型的数目和系统计算量.同时证明了闭环系统是有界输入有界输出(BIBO)稳定,并给出了跟踪误差的上界.与文献[8]相比,本文控制算法使得系统跟踪误差稳态值减小1倍.
1 问题描述
考虑如下离散时间被控对象:
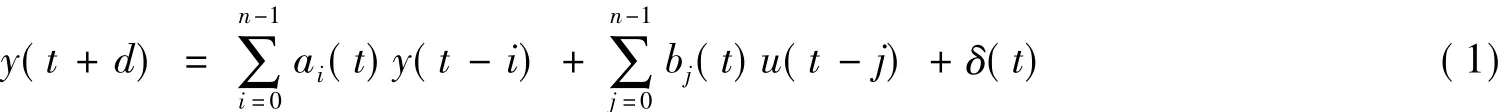
式中,y(t)和u(t)分别为被控对象的输出和输入;u(t)的系数b0不等于零;d是传输延时(d≥1);δ(t)为有界扰动.假设:
A1 参数ai(t),bi(t),i∈{0,1,…,n-1}为时间t的常值或分段常值函数,且相邻跳变时间间隔足够长;
A2 t变化时,参数向量[a0(t),…,an-1(t);b0(t),…,bn-1(t)]T在一紧集 Ω 中变化;
A3 对象阶次上限n和延时d已知;
A4 被控对象是最小相位系统;
为便于参数估计,将式(1)改写为如下递归形式:

式中,φ(t)=[y(t),…,y(t- n+1),u(t),…,u(t- n+1)]T;θ(t)=[a0(t),…,an-1(t),b0(t),…,bn-1(t)]T.本文的目的是对任意已知的有界参考输入y*(t),决定有界输入u(t),使得输出y(t)尽可能地跟踪y*(t),并保证闭环系统稳定.
2 模型集的建立
2.1 基于动态优化的固定模型集建立
固定模型集的动态优化由最优可行子集定位、动态覆盖两级寻优策略构成.
2.1.1 被控对象模型参数最优可行子集的定位
基于Localization方法,将参数集Ω分割为有限个子集的合集,且满足如下性质:① Ωi⊂Ω,Ωi非空,i=1,2,…,m; ②=Ω; ③ ∀i,i=1,2,…,m,∃θi∈Ωi(“中心”)和 ri>0(“半径”),使得∀θ∈Ωi,有‖θ-θi‖≤ri,θi和 ri的存在性由假设 A2 保证.
t时刻,若被控对象模型参数向量θ∈Ωi,则根据性质③和式(2)可得

如果式(3)不成立,则对象模型参数不属于子集Ωi,Ωi可被排除,只有满足式(3)的子集才接近被控对象的参数,即为可行子集.令I(t)代表t时刻被控对象模型参数所属的可行子集索引的集合,其初始化为I(t0)={1,2,…,m}.被控对象模型参数最优可行子集的定位过程如下:
① 对t>t0,计算
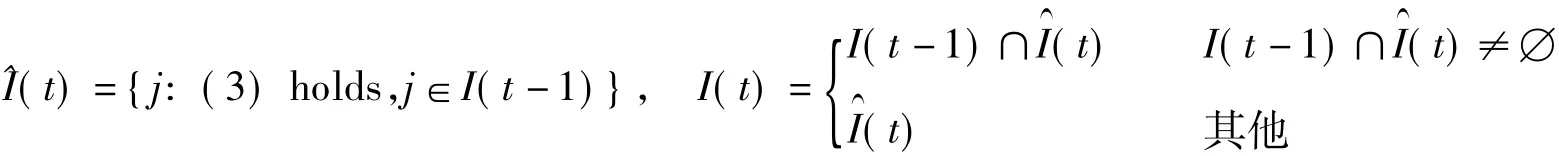
2.1.2 固定参数模型集的动态构造
设t时刻,被控对象模型参数所属的最优可行子集为Ωl,隶属于Ωl的模型参数向量可表示成

式中,v1,…,vn,…,v2n对应于对象模型的可变参数 ai和 bi,i=0,1,…,n -1.令 Ωl的中心 θl(θl=[v1-l,…,vn-l,…,v2n-l]T)为t时刻被控对象模型参数的最优估计,固定模型集的动态建立过程如下:
① 确定子集 Ωl中可变参数v1,…,vn,…,v2n的变化区间,即确定2,…,2n.
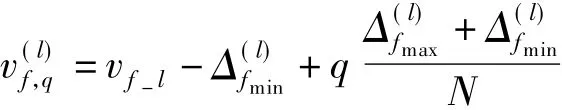
④将N个固定参数模型M1,M2,…,MN合成为t时刻动态创建的固定参数模型集.
为保证在各子集内动态生成的固定参数模型仍然落在其内部,下面的定理给出了一个充分条件.
证明 由向量2范数定义易得.
定义1 对象模型集由N个动态生成的固定参数模型Mi,i=1,2,…,N和常规自适应模型Ma1及可重新赋值自适应模型Ma2构成.
2.2 自适应模型
对于自适应模型,其参数采用如下带死区函数的投影算法[13]进行辨识:
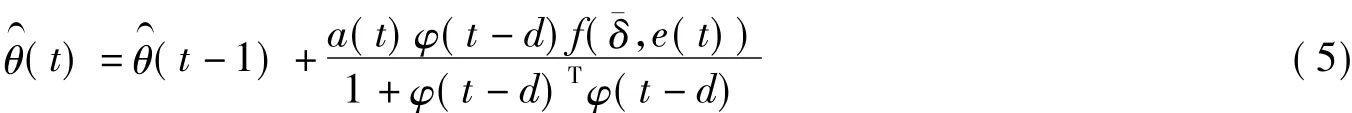
式中,0<a(t)<2;f(¯δ,e(t))是死区函数,e(t)是预测误差,满足
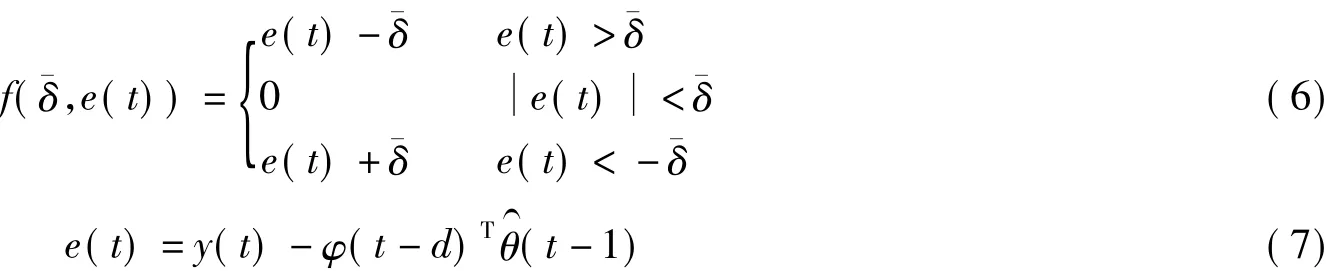
常规自适应模型Ma1用于保证系统的稳定性,其参数θa1如式(6)和(7)进行更新;可重新赋值自适应模型Ma2的参数θa2初值动态调整为距离被控对象最近的固定模型的参数,以获得更快的收敛速度.
3 多模型自适应控制器设计
令跟踪误差ec(t)=y(t)-y*(t),则

t时刻,若对象模型参数θ(t)已知,可由如下方程确定控制输入u(t):


基于模型集动态优化的多模型自适应控制器设计算法如下:
①构造数据向量φ(t-d),读入新的输出数据y(t).
②按2.1节的方法动态生成N个新的固定参数模型,并替换上一时刻生成的固定参数模型集.
④ 计算 Ji(t),i=1,2,…,N 和Jaj(t),j=1,2,令如果 Jl(t)(t)≤Jah(t)(t),令θ(t)=θl(t),如式(9)计算控制输入 u(t),并令; 否则,令=,如式(10)计算控制输入 u(t),并令
⑤ 令t=t+1,转①.
4 稳定性分析
引理1[13]对于时不变系统,参数估计算法式(5)~(7)满足:①,k 为正整数.
定理2 在假设条件A1~A5下,多模型控制器作用于系统(1)时,闭环系统BIBO稳定,即
1)若Jq(t)>0,则由引理1①可知必然存在一有限时刻T,使得∀t≥T,Jaj(t)≤Jq(t),j∈{1,2},此后,模型间的切换仅在自适应模型Ma1和Ma2间进行.简化起见,以下分析将省去自适应模型的下标aj.对任一自适应模型,由式(2)、(7)和(8)可得
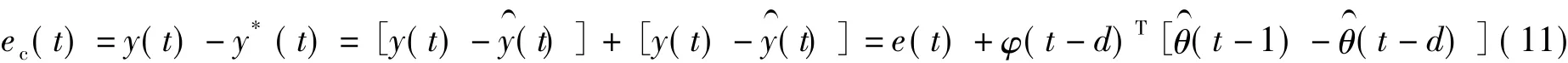
则
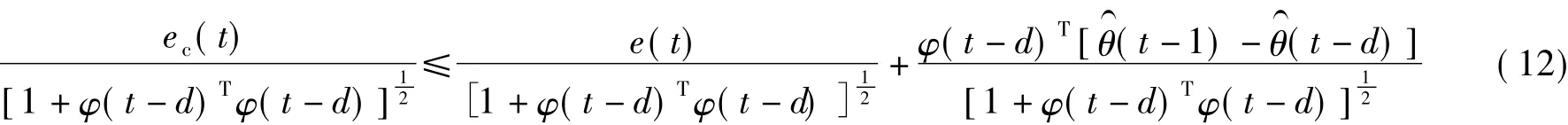
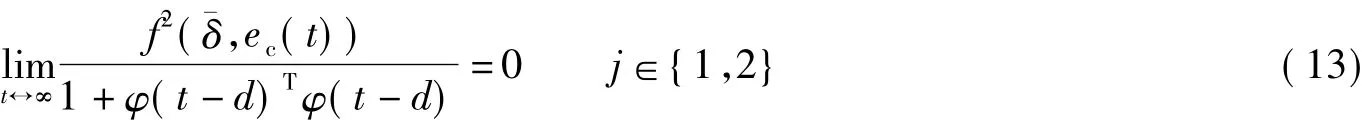
另外,由最小相位假设A4和式(6)可得
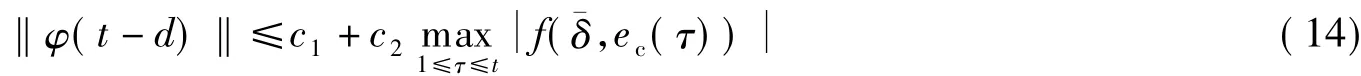
式中,0<c1<∞,0<c2<∞.由文献[14]中引理6.2.1可知式(15)和(16)满足引理条件,则可得的结论,即为定理2的结果.
2)若Jq(t)=0,参考文献[3]第Ⅲ部分及上述证明过程可得有界及即为定理2的结果.
文献[6]在研究同样的被控对象时得出的结论为:跟踪误差的稳态值是系统扰动项上界的2倍(见文献[6]定理2),而本文跟踪误差的稳态值即为系统扰动项的上界,系统的控制精度显著提高.
5 仿真
考虑如下离散时间时变系统:
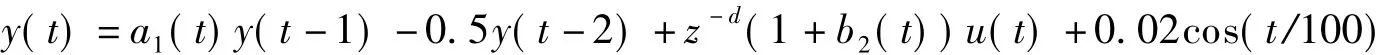
式中,d=2.参数{a1(t),b2(t)}未知时变,参考输入为y*(t)=2sin(πt/50).设未知参数{a1(t),b2(t)}在t=0时刻为{1.5,0.2},在t=100时刻变为{2.5,0.2},在t=200时刻变为{1,0.4},在t=300时刻变为{2,0.3}.根据a1(t)和b2(t)的可变范围,将对象模型参数集Ω分解为54个子集,各子集中心参数向量对应的 a1和 b2分别取为{0.95,1.15,…,2.35,2.55}和{0.15,0.2,…,0.35,0.4},N 取为 30.采用如下2种控制方案:①基于120个固定参数模型和自适应模型的MMAC;②基于本文算法的MMAC.在方案①中作者特意在参数{a1(t),b2(t)}的跳变值附近内构造固定参数模型.图1和图2分别为上述2种控制方案时系统的响应.
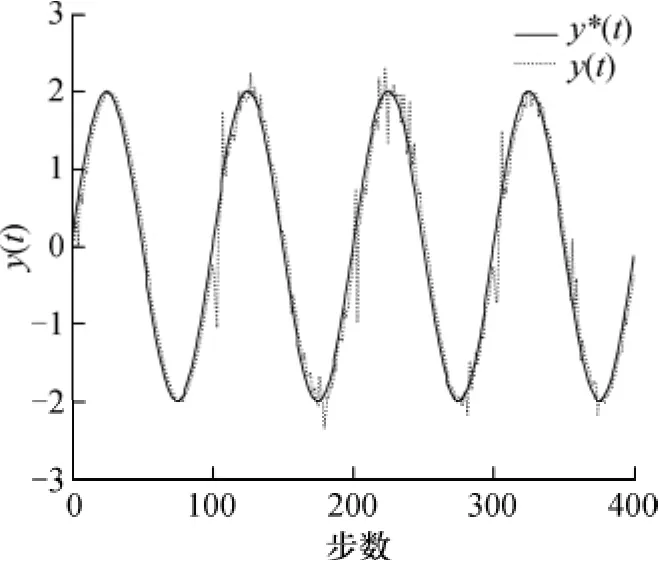
图1 控制方案1系统输出曲线
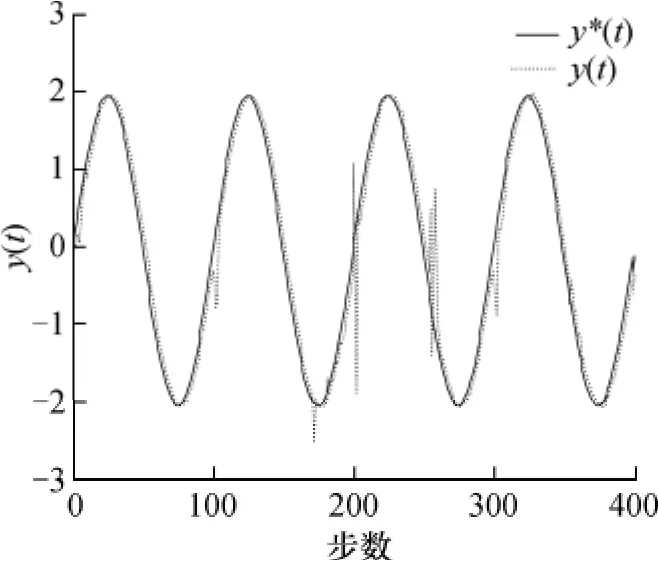
图2 控制方案2系统输出曲线
6 结语
针对一类具有界扰动和跳变参数的离散时间系统,本文提出基于模型集动态优化的多模型自适应控制算法,并证明了闭环系统的BIBO稳定性.与已有的研究结论相比,本文算法可使系统跟踪误差稳态值减小1倍.
References)
[1] Narendra K S,Balakrisham J.Improving transient response of adaptive control systems using multiple models and switching[J].IEEE Trans Autom Control,1994,39(9):1861-1866.
[2] Narendra K S,Balakrishnan J.Adaptive control using multiple models[J].IEEE Trans Autom Control,1997,42(2):171-187.
[3] Narendra K S,Cheng Xiang.Adaptive control of discrete-time systems using multiple models[J].IEEE Trans Autom Control,2000,45(9):1669-1686.
[4] Chen L J,Narendra K S.Nonlinear adaptive control using neural networks and multiple models[J].Automatica,2001,37(8):1245-1255.
[5] Narendra K S,Koshy G.Adaptive control of simple nonlinear systems using multiple models[C]//Proc of American Control Conference 2002.Anchorage,USA,2002:1245-1255.
[6] Narendra K S,Driollet O A.Stochastic adaptive control using multiple models for improved performance in the presence of random disturbances[J].Int J Adapt Control Signal Process,2001,15(3):287-317.
[7]Ippoliti G,Longhi S.Multiple models for adaptive control to improve the performance of minimum variance regulators[J].IEE Proc-Control Theory,2004,151(2):210-216.
[8]李晓理,王书宁.含有界扰动系统的多模型自适应控制[J].控制理论与应用,2003,20(4):577-581.Li Xiaoli,Wang Shuning.Multi-model adaptive control of system with bounded disturbance[J].Control Theory &Applications,2003,20(4):577-581.(in Chinese)
[9]王昕,李少远.多模型分层递阶自适应前馈解耦控制器[J].控制与决策,2005,20(1):17-22.Wang Xin,Li Shaoyuan.Hierarchical multiple model adaptive feedforward decoupling controller[J].Control and Decision,2005,20(1):17-22.(in Chinese)
[10] Maybeck P S,Hentz K P.Investigation of moving bank multiple model adaptive algorithms[J].Journal of Guidance Control Dynamics,1987,10(1):90-96.
[11]Zhivoglyadov P,Middleton R H,Fu M.Localization based switching adaptive control for time-varying discrete-time system [J].IEEE Trans Autom Control,2000,45(4):752-755.
[12]刘鲁源,吕伟杰,牟世忠.基于在线优化的切换多模型自适应控制[J].控制与决策,2002,17(4):407-410.Liu Luyuan,Lü Weijie,Mou Shizhong.Switching multiple model adaptive control based on online optimization[J].Control and Decision,2002,17(4):407-410.(in Chinese)
[13]王伟,顾兴源.两种自校正控制新算法及其应用[J].信息与控制决策,1989(1):48-51.Wang Wei,Gu Xingyuan.Two kinds of new adaptive control algorithms and applications[J].Information and Control,1989(1):48-51.(in Chinese)
[14] Goodwin G C,Sin K S.Adaptive filtering,prediction,and control[M].Englewood Cliffs:Prentice Hall,1984.
