电磁波多层媒质传播的[C]网络新理论
2010-08-23梁昌洪
梁昌洪,陈 曦
(西安电子科技大学天线与微波技术国防重点实验室,陕西西安 710071)
0 引言
本文是电磁场理论教学系列札记之十。
电磁波传播,特别是多层媒质的入射、反射和折射不仅是一个前沿的理论问题,而且还是一个重要的应用课题。探矿、测地和异物检测都离不开它们的基础——电磁波向多层媒质的传播。
本文根据三项原则构建出电磁波斜入射到媒质突变的平面边界的基本模型,它可以退化为垂直入射、导体和磁体边界等多种情况。将电磁波传播和网络理论有机结合,创新地提出了多层媒质的[C]网络理论,从而把困难的多层媒质传播转化为矩阵[C]级联,由应用实例得到一系列有用统一的结论,很值得作进一步探索和推广。
1 基本模型
不论入射、反射和折射,都涉及电磁平面波的传播。首先,本文对基本模型提出如下三项原则:
(1)将媒质突变的平面边界作为最基本单元;
(3)当入射角θi,反射角θr和折射角θi均为0°,即θi=θr=θi=0°,问题应该退化成垂直入射情况。
必须指出:正因为有原则(3),使本文的结果与大多数著作有所差异[1-12]。图1给出了基本模型的两种情况。
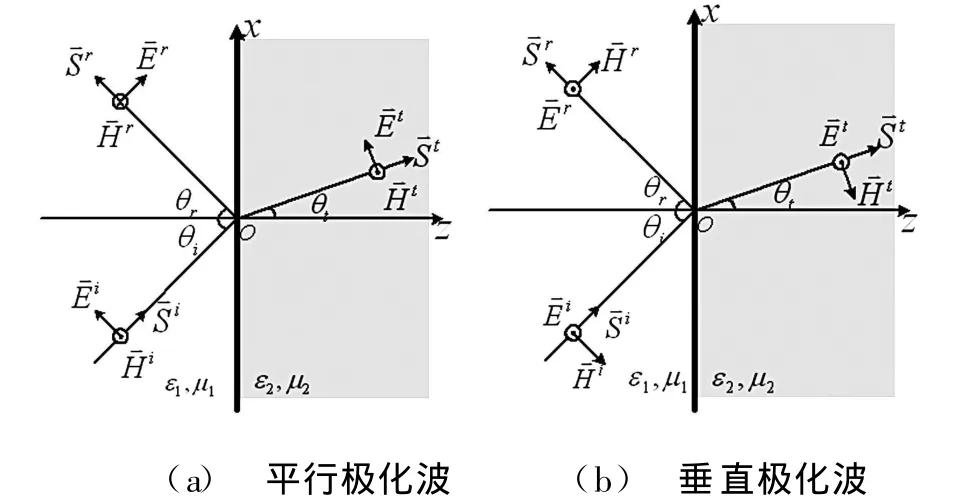
图1 平面波斜入射平面边界作为基本模型
[情况1]平行极化波
这种情况下,电磁场在平面边界的匹配条件为
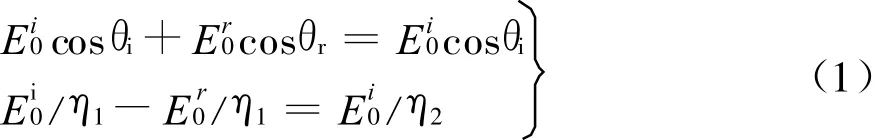

很易得到

式中,已计及Fermat原理θi=θr。由式(3)很易得到

[情况2]垂直极化波
这种情况下,电磁场在平面边界的匹配条件对应为
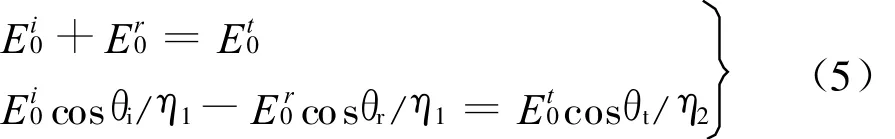
类似可得反射系数 Γ⊥和折射系数T⊥分别是
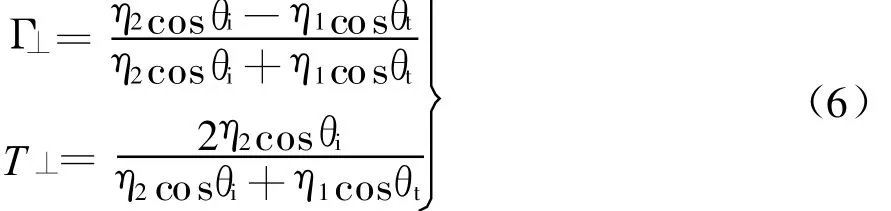
根据确定基本模型第(3)原则,考察式(3)和式(6),果然在垂直入射时 ,即θi=θr=θt=0°,统一有
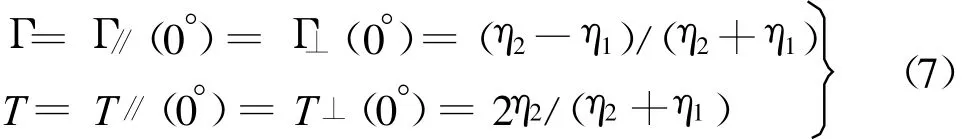
并且有关系:

我们还应该进一步解释把电磁波斜入射平面界面作为基本模型的深层次原因:它不仅可包含垂直入射情况,而且可以概括第二媒质是理想导体,即电壁情况。这时需令η2=0,有
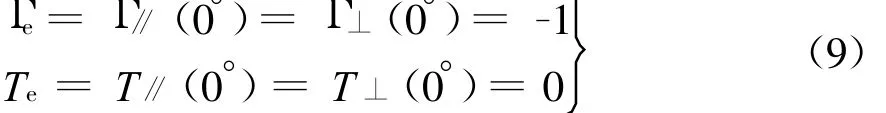
和第二媒质是理想磁体,即磁壁情况,这时η2※∞,于是
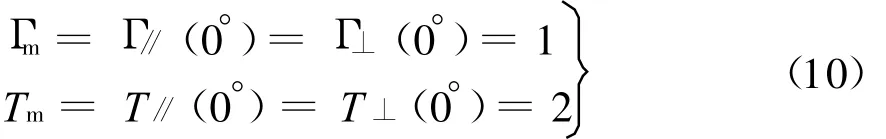
读者或许对式(10)中Tm=2有些疑惑不解。实际上只需注意到本文的Γ和T都是针对电场的反射和折射,后边可清楚看出,完全满足能量守恒关系。
2 特殊角度
平面电磁波入射到界面发生反射和折射时,有两个特殊角度值得重视:无反射Brew ster角θB和全反射临界角θc。
[情况1]无反射Brewster角θB
对于平行极化波,由无反射条件给出

计及Fermat原理,有

易得Brew ster角为
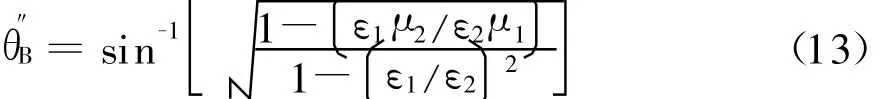
而对于垂直极化波,这时的无反射条件是

对应的Brewster角为
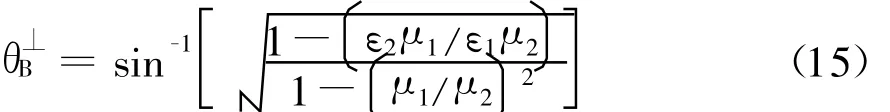
特别应该指出,对于电介质,也即μ1=μ2,这时垂直极化波不可能出现Brewster角,只有在平行极化波情况下才能出现无反射现象的Brewster角。
[情况2]全反射临界角θc
由式(3)和式(6)很易看出,只要满足

则必然会出现全反射,即这时有

且由式(16)可具体给出

这时可知

它意味着电磁波只沿表面传播,且不进入第二媒质,具体发生全反射的临界角θc与平行极化波还是垂直极化波无关,为

因此,产生全反射的条件有

特别对于μ1=μ2的电介质,更进一步得到

换句话说,只有光密媒质入射到光疏媒质界面才会出现全反射现象,正是应用这一原理产生了近代的光导纤维。
3 电磁波传播[C]网络
为了研究斜入射多层媒质的复杂情况,本文把电磁波传播与网络理论有机的结合起来,提出[C]网络理论。见图2所示。

图2 电磁波传播[C]网络
作为一个典型实例,我们研究[C]网络如何表示传播时媒质的突变界面。
从对称端口观点看:b1,b2分别表示端口 ①和端口 ②的电场反射,而a1,a2则表示相应的电场入射,采用矩阵有
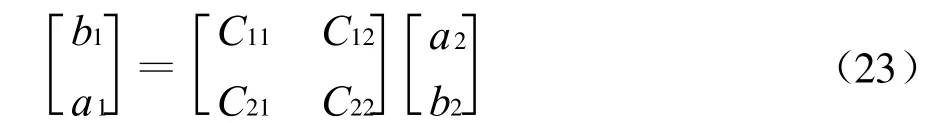
从端口 ①至端口 ②的广义传输角度看
a1——表示端口 ①的入射;a1=
b1——表示端口 ①的反射;b1=
b2——表示端口 ②的折射;b2=
a2——对于如图2的单层媒质突变网络,有

而对于多层网络,则a2表示第二层的反射。
[情况1]平行极化波斜入射
由式(1)和式(2)并考虑各层对称形式,可得

进一步写出
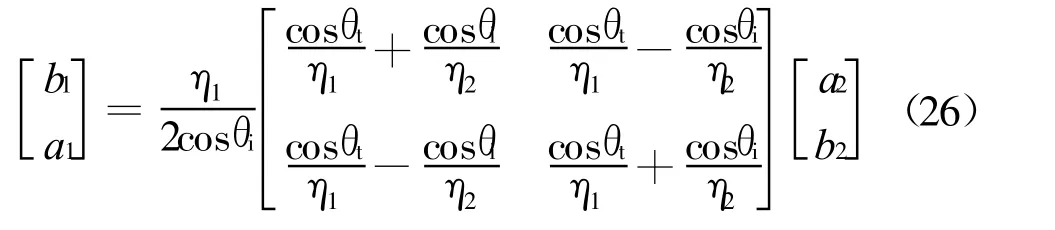
为便于推广,引入

即可给出平行极化波的电磁波[C∥]矩阵,为
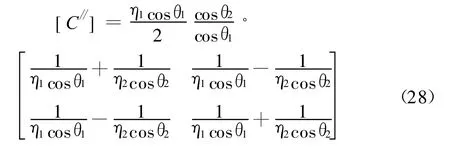
特别是,对于只有单层突变媒质情况,计及a2=0,
可具体写出
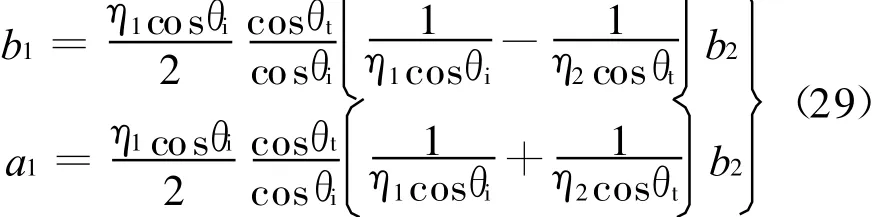
很易得到

可见,完全与式(3)结果一致。
[情况2]垂直极化波斜入射
同样由式(5)及对称性考虑,又得

进一步写出
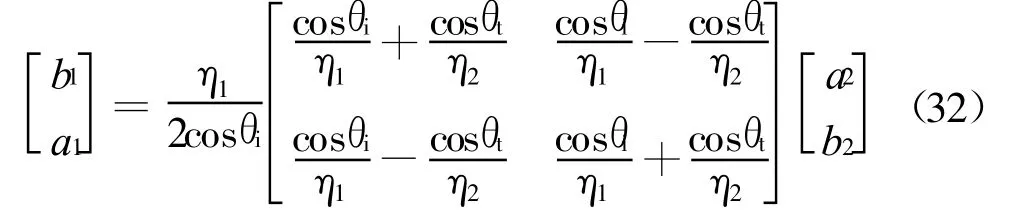

并得到垂直极化波[C⊥]网络有对于只有单层突变媒质情况,a2=0,可给出
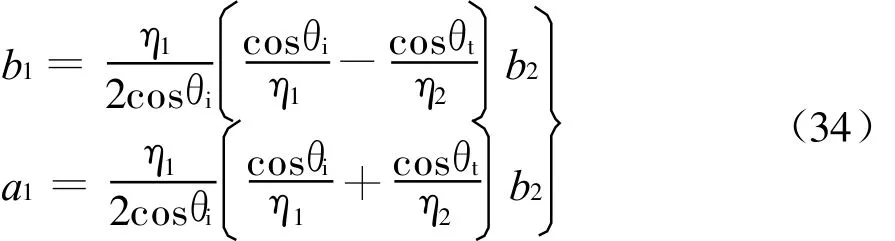
最后得到

可见,同样与式(6)结果完全一致。
[情况3]垂直入射情况
只要计及θ1=θ2=0°时,式(28)和(33)均成为同一垂直入射网络,为
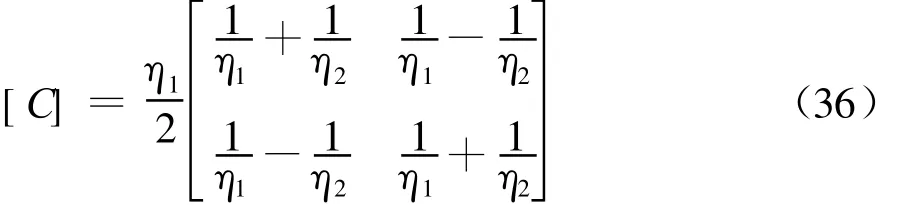
[情况4]统一[C]网络
本文引入统一阻抗Z符号,定义是

于是,可写出统一的[C]网络

[情况5]波传输段[Cl]

图3 波传输[cl]段网络
由定义写出
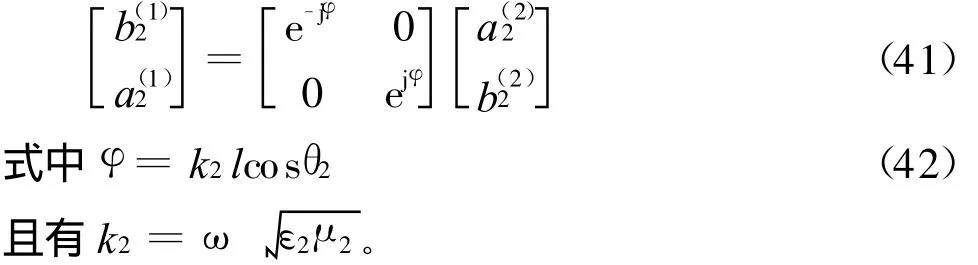
4 工程实例
电磁波传输[C]网络的最大特点是它满足级联条件,如图4所示的n个网络C1,C2,……Cn级联,则总网络很易写出


图4 n个网络C1,C2,……Cn级联
十分明显,这一特性十分适合多层媒质的研究课题。
本文将给出工程应用中三层无耗媒质情况,如图5所示。采用[C]矩阵可写出


式中,对于平行极化波,有

于是可得到

由此很易导出
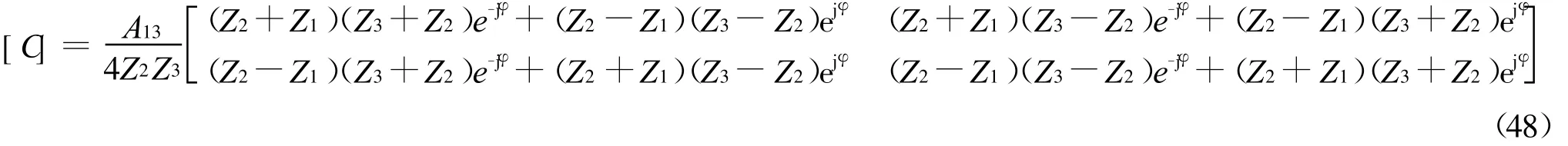
对于a3=0,有
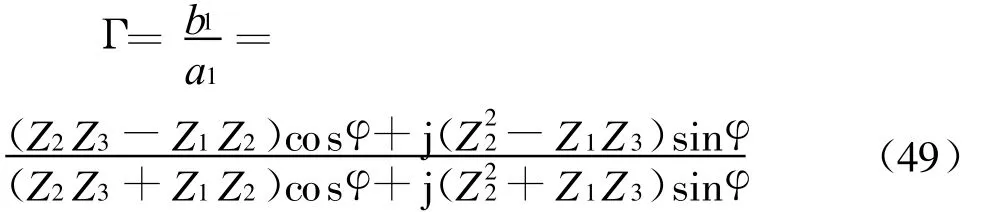
特别需要指出:上式反射系数 Γ不论对于垂直入射,平行极化波还是垂直极化波的斜入射,形式完全统一,只是Z 分别对应η,η∥,η⊥。
如果进一步引进输入阻抗Zin:
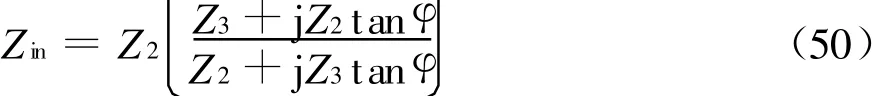
则式(49)可进一步表述为

与正确结果完全一致[2]。
另一方面,折射系数T为
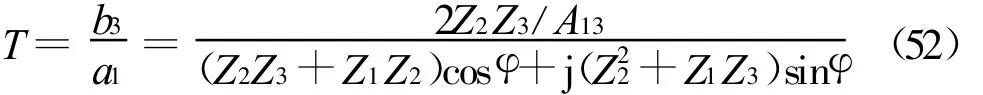
对于垂直入射,平行极化波和垂直极化波斜入射,Z和A13表述有所不同。
5 能量守恒
由于本文所及限于无耗媒质模型,所以在电磁波传播过程中入射波,反射波和折射波的功率之间,必须存在着能量守恒关系。
首先,让我们考察单层无耗媒质突变情况,由式(3),式(6)和式(7)可统一写出

具体对于垂直入射情况,A12=1有

对于垂直极化波斜入射情况,由于A12=1依然成立,于是有

最后,对于水平极化波斜入射情况,这时由于A12=cosθ2/cosθ1,而 Z1/Z2=η1cosθ1/η2cosθ2,又可得

发现十分奇妙的是,能量关系的结果是唯一且相同的。
现在,让我们进一步观察三层无耗媒质情况。只要注意到式(49)和式(52),即可知
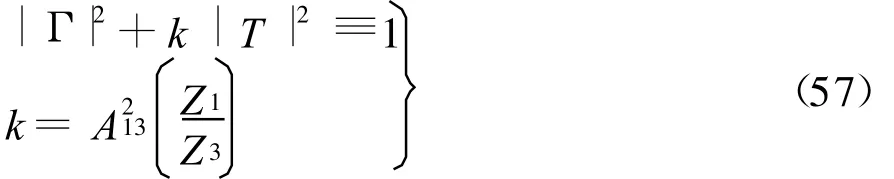
这时的能量守恒关系与第二媒质层 φ=k2lcosθ2无关。它从概念上讲是十分自然的。因为k也可写成
这样,我们有理由推广到n层无耗媒质情况,一般的能量守恒关系是

6 结语
如果说本文还略有新意,那么可以说是电磁波和网络理论的有机结合,它把多层媒质问题转化为矩阵理论,清晰而简单。
关于有耗媒质或非互易多层媒质拟由另文报道。
[1] 毕德显.电磁场理论[M].北京:电子工业出版社,1985
[2] 杨儒贵.高等电磁理论[M].北京:高等教育出版社,2008
[3] 牛中奇,朱满座,卢智远,路宏敏等.电磁场理论基础[M].北京:电子工业出版社,2001
[4] 谢处方,饶克谨编.电磁场与电磁波[M].北京:高等教育出版社,2006
[5] 王家礼,朱满座,路宏敏.电磁场与电磁波.西安:西安电子科技大学出版社,2000
[6] 曹伟,徐立勤.电磁波与电磁理论.北京:北京邮电大学出版社.1999
[7] 陈重,崔正勤.电磁场理论基础.北京:北京理工大学出版社.2003
[8] 冯恩信.电磁场与波.西安:西安交通大学出版社.1999
[9] 林为干等.电磁场理论[M].北京:人民邮电出版社,1984
[10]Chew W.C.Waves and Fields in Inhomogeneous Media[M].New York:Van Nostrand Reinhold,1990
[11] Wait J.R.Electromagnetic Waves in Strarified Media[M].London Oxford University Press,1994
[12]Kong.J.A.Electromagnetic Waves Thory(1),(2),(3)[M].影印版。北京:高等教育出版社,2006
