二级新型悬臂式挡土墙有限元分析
2010-08-21王景环傅绍娟
王景环 傅绍娟
随着经济的发展,铁路、公路、水利等工程上支挡结构大量出现,对支挡结构的要求越来越高,综合考虑的因素也较多,因此在挡墙的发展方向上,将更多的考虑结构的轻型化、机械化,充分发挥建筑材料的强度性能等特点,而悬臂(扶壁)式挡墙能满足以上要求,同时还能依靠墙后填土来维持稳定,适用一定的交替变形,种种特点说明了二级悬臂式挡墙必然得到更广泛的发展。同时,为了进一步扩大这种支挡结构应用范围,本文将探讨二级新型悬臂式挡墙这一新形式,为今后的实际工程提供一定的理论基础。
1 计算模型选用
采用平面应变的有限元进行分析,同时考虑挡墙与土之间的接触,在挡墙实际墙背与填土之间设置接触对,选用单元类型的原则是:用最少数目的单元达到最高的计算精度且使运算时间最少,本分析中采用4节点四边形等参数单元将分析范围进行有限元剖分。悬臂式挡墙模型底面长度为40 m,约为挡墙墙底板长度的10倍,不考虑挡墙墙踵前土的作用,墙前距离为9 m,墙顶及填土的总长为31 m,在划分网格时采用映射网格划分方法,在可能的填土范围网格进行加密处理;二级悬臂式挡墙模型大致同悬臂式挡墙模型,在挡墙计算墙面内加密网格。本文采用ADINA在计算时所用的是平面4节点等参数单元和Gauss积分方式[1]。
2 计算参数
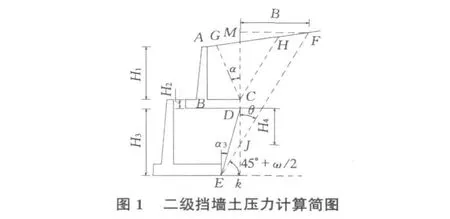
挡墙实际墙背与填土之间的摩擦系数为0.3,其他参数见表1,计算简图见图1。
3 边界条件
二级悬臂式挡墙有限元网格边界约束条件:顶部表面自由;两侧边界水平约束;底边界竖向均约束。

表1 计算参数
4 有限元结果分析
1)实际墙背位移。从上墙立板水平位移中可以看出,上墙墙顶的水平位移较大,达到0.7 mm,朝填土方向移动,而墙底水平位移则较小,基本上反映了上墙水平位移的线性变化,结合底板的竖向位移,可以明显的看出,上墙是绕墙底某点发生了转动并同时伴随着挡墙的下沉。在底板的位移图中,墙趾端处沉降小,而墙踵端处沉降相对较大,反映出作用在挡墙底板的竖向应力的不均衡性,挡墙的平均竖向位移为-6.5 mm左右。上墙竖向位移比水平位移要大很多,反映出挡墙基底的承载能力对挡墙位移的影响比较大。下墙的水平位移倾向虽然与上墙类似,但下墙是墙顶水平位移小,而墙底相对来说位移要大一些,而且方向是背离填土方向移动的,反映出下墙与上墙不同的位移方式,结合竖向位移来说,下墙是绕墙顶某点转动并伴随竖向沉降,竖向沉降趋势同上墙类似,墙趾位移小,而墙踵端较大。
2)实际墙背和整体作用下计算墙面水平应力。从水平应力云图中可以发现:上墙墙底板内、下墙墙踵板内产生了较大正应力,应该是摩擦所致,在上墙墙趾与立板交接处产生了较大的压应力,在二级挡墙后的水平应力分布较均匀,下墙墙趾处土体中应力相对较大。从实际墙背即上下墙立板处应力图可以看出,同是类似于三角形的土压力[3]分布,上墙在0.75 m处应力发生转折,随后随墙高的增加而减小;下墙也在0.75 m处应力发生转折,随后随墙高的增加而减小,在2.25 m处有个极值点。
从立板的应力图可以看出,上墙立板的土压力为13.9 kN/m,解析计算结果为9.68 kN/m;下墙立板土压力为37.5 kN/m,解析计算结果为33.725 kN/m;从对比结果中可以看出,有限元计算结果同解析计算结果比较接近,说明上下墙的局部简化计算有一定的合理性。
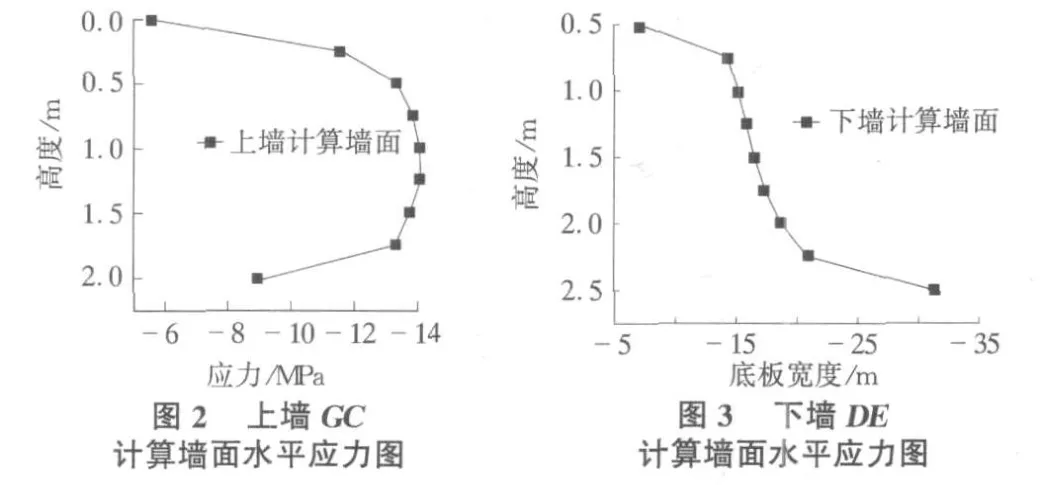
从图2,图3中可以看出,作用在上下墙计算墙面的应力分布有明显的区别,上墙计算墙面应力0.5 m处以上随墙高增加而增加,在0.5 m~1.75 m处应力呈抛物线分布,在2 m处应力又变小,整体形态上类似于抛物线分布;而下墙计算墙面有明显梯形分布特点,下墙计算墙面顶点处有一定的应力作用,很明显是上墙墙底应力传递所致,下墙计算墙面最大应力发生在底部,而同下墙立板底部处应力比较得知:下墙计算墙面与下墙立板之间应力相差较大,也就是说,下墙计算墙面与下墙立板之间所构成的填土在传递作用力时与填土高度成线性变化有一定的区别。而上墙计算墙面应力与上墙立板应力相比并不相差很大,可能是跟挡墙的高度[4]有关。从应力分析中可知,二级挡墙上墙同单级挡墙的分析模式区别不大,而下墙在做局部分析的时候可以采用简化的解析计算方法[5]。
3)强度发挥系数等值线。从图4中可以看出墙后填土基本上都处于弹性状态,在上下墙实际墙背范围,填土的强度发挥系数变化范围较大,在靠近上墙墙顶处,强度发挥系数从等值线上可以看出将近0.7,下墙强度发挥系数最大的地方也在靠近墙顶处,即0.6 m处左右,与实际墙背上的土应力分布有些类似,应该是此处土应力较大所致,而且在靠近下墙底部处,强度发挥系数变化也较大;从图4中也可以看到,上墙墙底土的强度发挥比较均匀,而下墙相对来说要变化大一些,在墙趾处有较大的强度发挥,可能的原因是下墙除了需承受土的自重以外,还需承受上墙传递下来的部分土压力作用。

5 结语
1)二级悬臂式挡墙上墙应力分布,跟挡墙的高度、刚度和位移有关,具体相关性有待进一步的考虑,而下墙立板的应力类似一般三角形分布,但墙顶处是有相对较大的应力作用的,在以后的设计中可以采用本文简化的计算方法得到下墙立板的土压力分布。2)二级悬臂式挡墙上下墙计算墙面的土压力分布有比较大的区别,上墙计算墙面应力分布呈抛物线形状,而下墙更加接近梯形分布,同下墙立板应力区别较大,在设计二级悬臂式挡墙的时候考虑整体与局部的土压力作用是很有必要的。3)在本例中,从有限元计算结果来看,其土压力值比解析计算中的土压力值要小,而且呈现出非线性变化的特点,计算表明:墙体位移和土压力要受到墙体刚度、墙背粗糙程度、填土弹模等因素的影响,其中在填土一定的情况下,与墙体刚度最为密切。4)从有限元分析结果来看,二级挡墙上墙的卸荷作用比较明显,与解析计算结论相符合,与国内目前已经采用的倒F形挡墙卸荷作用类似,同时土的自重在二级挡墙中得到了充分的利用,因此在工程运用中需保证填土的压实度,尤其是上下墙过渡区域。5)从解析计算和有限元比较结果来看,二级悬臂式挡墙采用类似于有减压平台的挡土墙土压力计算方法,与有限元结果并无太大出入,吻合较好,在今后可能的二级悬臂式挡墙实际工程中,可以采用这种方法进行土压力的计算以作参考。
[1]谢康和,周 健.岩土工程有限元理论与应用[M].北京:科学出版社,2002.
[2]顾慰慈.挡土墙土压力计算[M].北京:中国建材工业出版社,2001.
[3]钱家欢,殷宗泽.土工原理与计算[M].北京:中国水利水电出版社,1996.
[4]张仪萍.沉降的灰色预测[J].工业建筑,1999,29(4):45-48.
[5]鲍尔斯.土力学计算[M].北京:人民交通出版社,1982.
[6]Bakeer,R.M.,Bhatia,S.K..Earth pressure behind a gravity retaining Wal.l Int.J.Numer.Ana.l Methods in Geomech,1989(13):665-673.
