递归算法的参数设置

王宏伟 赵国庆

(西安电子科技大学 电子对抗研究所 陕西 西安710071)

1.引 言

传统的时频分析方法包括短时傅立叶变换(STFT)[1],维格纳变换(WVD)[2],小波变换(WT)[3],滑动 DFT[4-6],滑窗 FFT[7-9]等 。STFT 受测不准原理制约,时、频分辨率较差;WVD存在交叉项干扰;WT计算量大;单点滑动DFT运算速度快,但数据不能在时域加窗以减小频谱泄露[6];滑窗FFT由于使用了技术成熟的FFT器件,运算速度较DFT快,但只能毫无选择地计算出全部离散频率点的频谱。

递归算法可以有选择地计算局部频段的连续频谱,实时地进行时频分析,时域参数测量和频域参数测量。通过工作参数的设置与调整,表明递归算法不仅时间分辨率和频率分辨率可以调整,而且所分析的频率或频段可灵活设置。该算法具有运算速度快、数据存储量少、资源占用量与工作参数的变化无关等特点。

2.递归算法的介绍

2.1 基本递归单元的结构

图1为递归算法的基本递归单元(单一通路)结构图,时域数据流经数据整理,获取以n时刻为起点,长度为 N的一段时域数据帧,加窗滤波减少频谱泄露(一般选择汉宁窗,窗口宽度为 N),进入递归运算,N次循环迭代后,乘以权系数e便得到了n时刻起长度为N的时域数据在频率点f处的离散傅立叶变换系数y(n,f),其中 fs为采样频率。

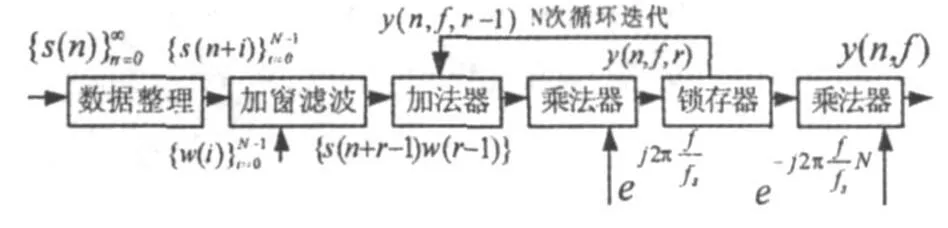
图1 基本递归单元的结构图

递归算法满足循环迭代公式

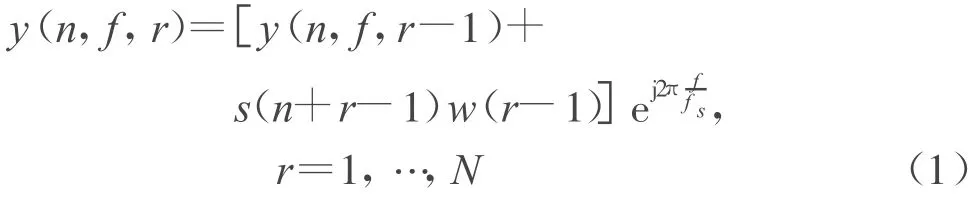
式中:r为迭代次数;y(n,f,r)为第r次迭代结果。令初始状态y(n,f,0)=0,则

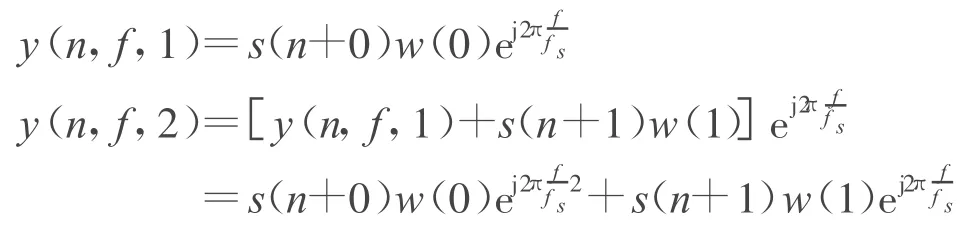
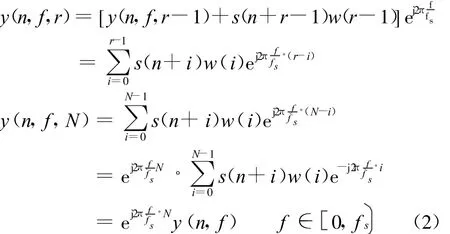
那么

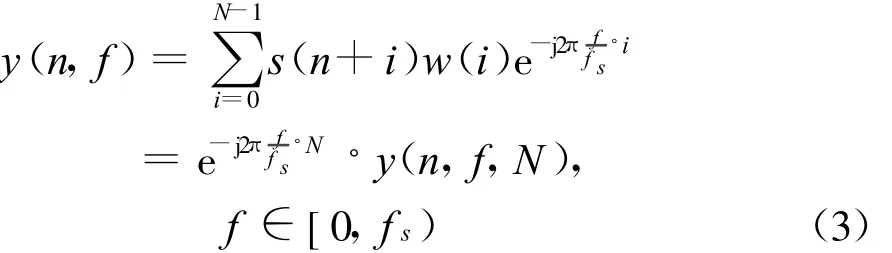
在表达式y(n,f,N)中:n为时域数据帧的起始时刻;N为循环迭代次数,其值等于参与循环迭代运算的数据帧长度和窗口宽度;f为所分析频率,在频率轴上可以选择任意实数值。当·k时,,此处 k=0,1,…,N-1,式(3)可改写为

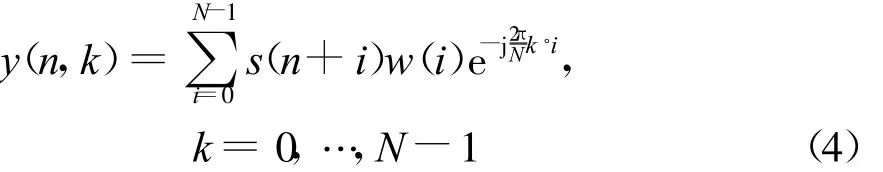
式(4)就是传统的滑窗FFT运算,它得到了离散频率点k处的傅立叶变换系数。表明式(4)只是式(3)的特例,式(3)得到的是任意实数(包括 f s/N整数倍)频率点的离散时间(DTFT)傅立叶系数,而式(4)像滑窗FFT算法一样只能得到 f s/N整数倍频率点的离散傅立叶(DFT)系数。

递归算法是建立在有限长数据的离散傅立叶变换基础上的,因此,具有和离散时间傅立叶变换相似的性质,包括下列性质:

1)线性性质。递归算法属于线性变换,不会产生新的频率分量,不会受交叉项干扰。

从滤波器角度看,这种带反馈结构的基本递归单元可以被看成用一阶 IIR滤波器实现的 N阶FIR滤波器。

2.2 多路递归算法的结构

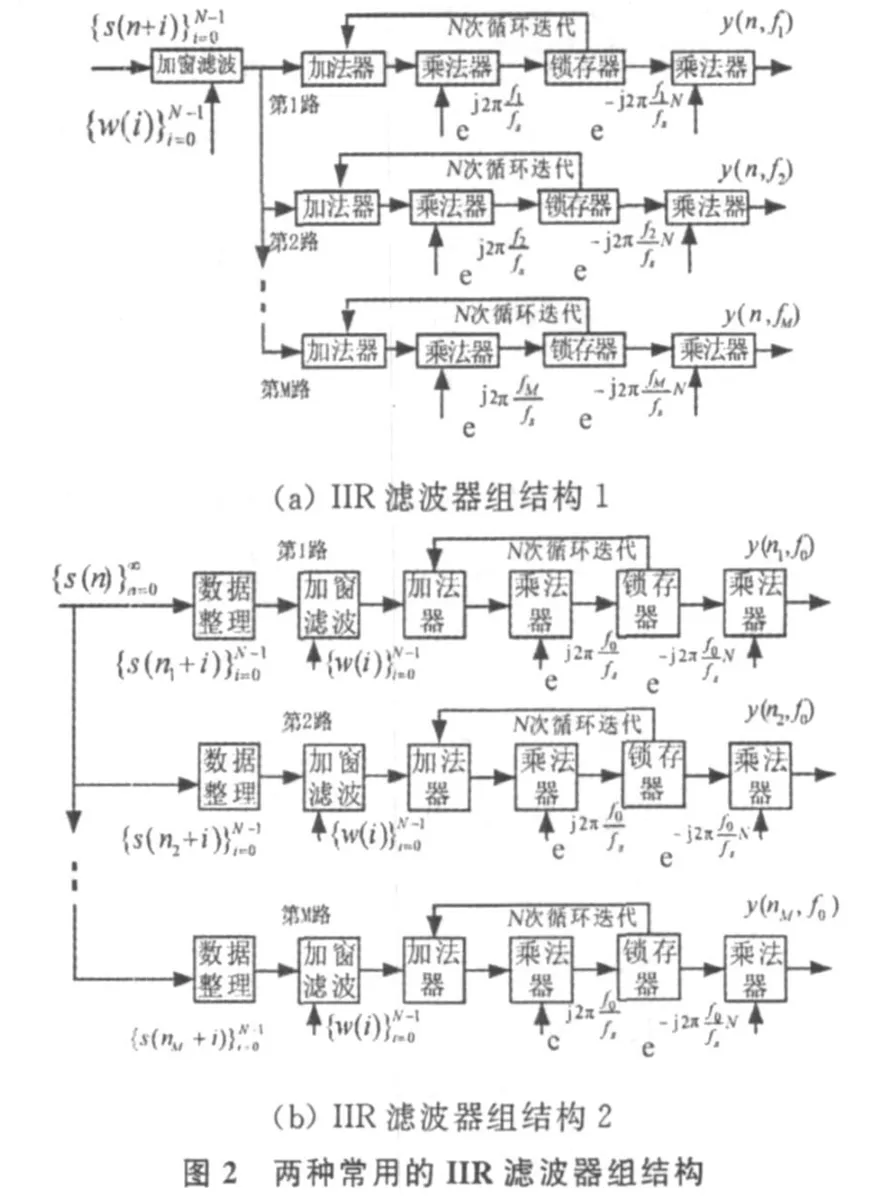
虽然通过对工作参数n,f,N的设置和调整,整个二维时频谱的计算完全可以由单一通路完成,但是为了提高时频分析效率,需要将多个通路集成为不同结构的IIR滤波器组,如图2,文中给出了两种结构。滤波器组内部各通路相互独立,并行工作,通路数目M根据需要可独立增减和使用。

如果将IIR滤波器组内各通路的参数 N和n设置为相同规律变化,而各通路的参数 f m,m=1,…,M不相同,结构如图2(a)。设计图2(a)结构的滤波器组时,可将数据整理工作移到滤波器组外进行。

根据实际需要,利用图2(a)结构,可以有选择地计算任何时刻起点n的一帧N长时域数据对应的任意局部频段的谱线,比只能计算全部离散频谱的FFT算法更加经济有效,更加灵活。

利用各通路的独立性,如果将所有通路都设置为对某特定频率点 f 0(一般选信号中心频率或载频)的递归运算,N仍采用相同规律变化,而各个通路所利用的数据帧起点nm不同,m=1,…,M,结构如图2(b)。各通路初始的数据帧起始时刻 的设置可参考

循环流水作业时,各通路数据帧的起始时刻nm,j可设置为

式中:M 为通路数目;j=1,…,∞;nm,j表示第m路第j级流水作业时数据帧的起始时刻;n0为研究开始时刻点;d为相邻通路数据帧起始时刻的时间间隔,即相邻通路数据帧间滑移量,d∈1,…,N.时域数据流经图2(b)结构处理后得到某特定频率f0信号不同时刻点的频域信息,满足时间分辨率的前提下,用门限检测的方法就可获取信号的起始时刻,终止时刻,持续时间等时域信息。

由于图2(b)结构的各通路以时空转化方式,将长时间跨度的时域数据转化到并行的通路空间上,并行循环流水作业或依次循环流水作业,并且相邻通路数据帧间滑移量d可以调整,因此,运算的实时性、时域参数测量精度与整体运算量之间的矛盾问题容易协调解决。

2.3 多路递归算法的特点

在图2中,每个通路的计算量仅为N+1次复数乘(加)。由于各通路的并行工作,因此,多路递归算法的计算量也为 N+1次复数乘(加),相比于滑窗FFT算法[9]的 N log2N次复数乘(加),计算量小。

通路数目M较多时,从宏观上看,滤波器组规模庞大,但每一路的递归运算只需要一个加法器、两个乘法器和一个锁存器,通路内部器件简单,各通路结构相同,易于多个通路集成,数据存储量少,资源占用量与工作参数n,f,N的变化无关。

通过对工作参数n,f,N的设置与调整,结合具体实例来详细讨论递归算法的其它特点。

3.参数设置与调整

3.1 参数 f的设置与调整——实现信号检测、频谱细化分析、频域参数测量

设有同时到达的两个单载频脉冲信号,一个信号的载频 f 1=30 MHz,占空比40%;另一个信号的载频 f 2=30.8 MHz,占空比60%;脉冲重复频率均为 fp=100 k Hz,采样频率为 fs=100 MHz;信噪比SNR=15 d B;图2的两种IIR滤波器组内单一通路的集成数目M均为100。

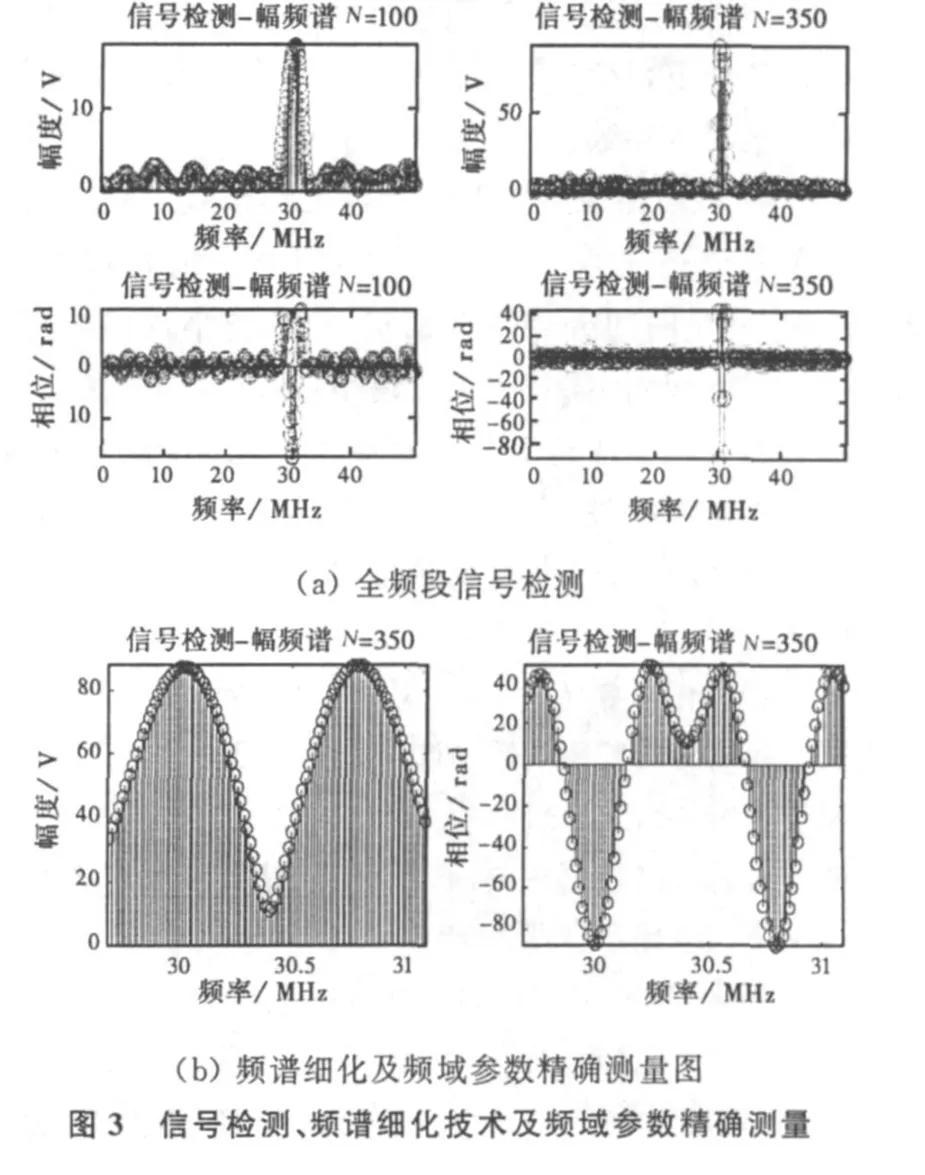
信号检测的目的是检测在有效全局频段0～50 MHz内有无信号,存在信号的数目及其所在的局部频段。若指定相邻谱线间隔Δfgrid=0.1 MHz,那么实际需要的通路数目M=50/0.1=500＞100路。解决方案1:并行方式。将五块图2(a)结构的IIR滤波器组并行使用,各通路频率分别设置为 f m=0.1×m(MHz),通路编号m=0,1,…,499。解决方案2:时分方式。仅用一块图2(a)结构的IIR滤波器组,对于输入的每一帧数据,数据不变(d=0)仅改变各通路被测频率,运算五次。其中第l次将各通路频率分别设置为 f m=0.1·(l-1)+m/2(MHz),l=1,…,5,m=0,1,…,99。当其它参数:n=0,N分别取100和350时,得到全频段信号检测的幅频谱和相频图如图3(a)。

由图3(a)可知,在30 MHz左右的局部频段存在信号,并且只有当循环迭代次数N比较大时才能可靠地发现此局部频段存在两个信号。

为了进一步测量信号的频域参数,调整各通路频率,对有信号(或感兴趣)的局部频段,进行频谱细化分析。局部频段分析时,各通路频率设置可参考下式

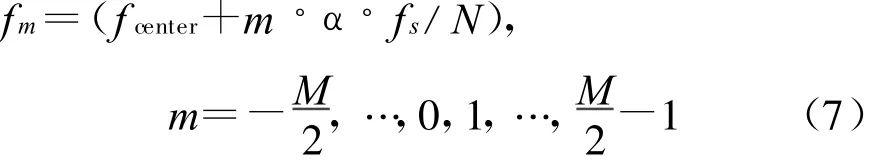
通过对被测频段中心的调整并配合频谱细化技术,可以使相邻谱线间隔Δf grid=α·f s/N(调整频谱细化系数α)变得很小(满足频率分辨率的前提下,谱线间隔Δfgrid越小,频域参数测量精度越高),得到一帧可移动中心位置(调整)的可变局部频段的近似连续频谱,从而可以分析任意感兴趣的局部频段的频谱细节。若不考虑噪声、频谱混叠等因素的影响,利用图3(b),理论上频域参数的测量误差可以做到趋于零。

虽然利用递归算法可以完成全频段信号检测任务,但需要消耗大量资源或以牺牲部分实时性为代价。而在局部频段分析时,无须增加资源或同帧数据多次利用便可保证信号实时检测、频谱细化分析和频域参数精确测量。可见,递归算法比较适合局部频段的时频分析。在实际应用中,也可配合其它算法先进行频段粗引导,再用递归算法进行局部频段精细分析。

3.2 参数n的设置与调整——实现二维时频谱分析和时域参数的实时测量

前面用一帧数据已获得某时刻起N长时域数据对应的频谱分布,随着参数n的连续变化(由数据帧的滑移量d体现,d∈{1,2,…,N}),计算不同起始时刻数据帧(N保持不变)对应的频谱分布,联合起来便可以得到二维时频谱图。

仍以2.1节中的两脉冲信号为例。当工作参数:f m=(30.4+m·0.15·f s/N)(MHz),m=-50,-49,…,49;N=350;d=10时得到的二维时频图,如图4。

在二维时频图中,时频分析系统可以根据各路输出结果,调整工作参数,在显示器上观察不同参数条件下,信号实时动态变化的特点。系统也可以在脱机条件下,针对信号特点,寻找最佳工作参数并精确测量时频参数。

图2(a)结构虽然采用并行工作模式,每帧数据对单一通路而言,计算量不大,但滑移量d取得较小时(满足时间分辨率的前提下,d越小,时频谱网格的时域间隔Δtgrid=d/fs越小,则时域参数测量精度就越高),总体运算量变得很大,难以保证二维时频分析的实时性,尤其是时域参数实时测量。利用图2(b)结构来解决单载频信号时域参数实时测量问题。

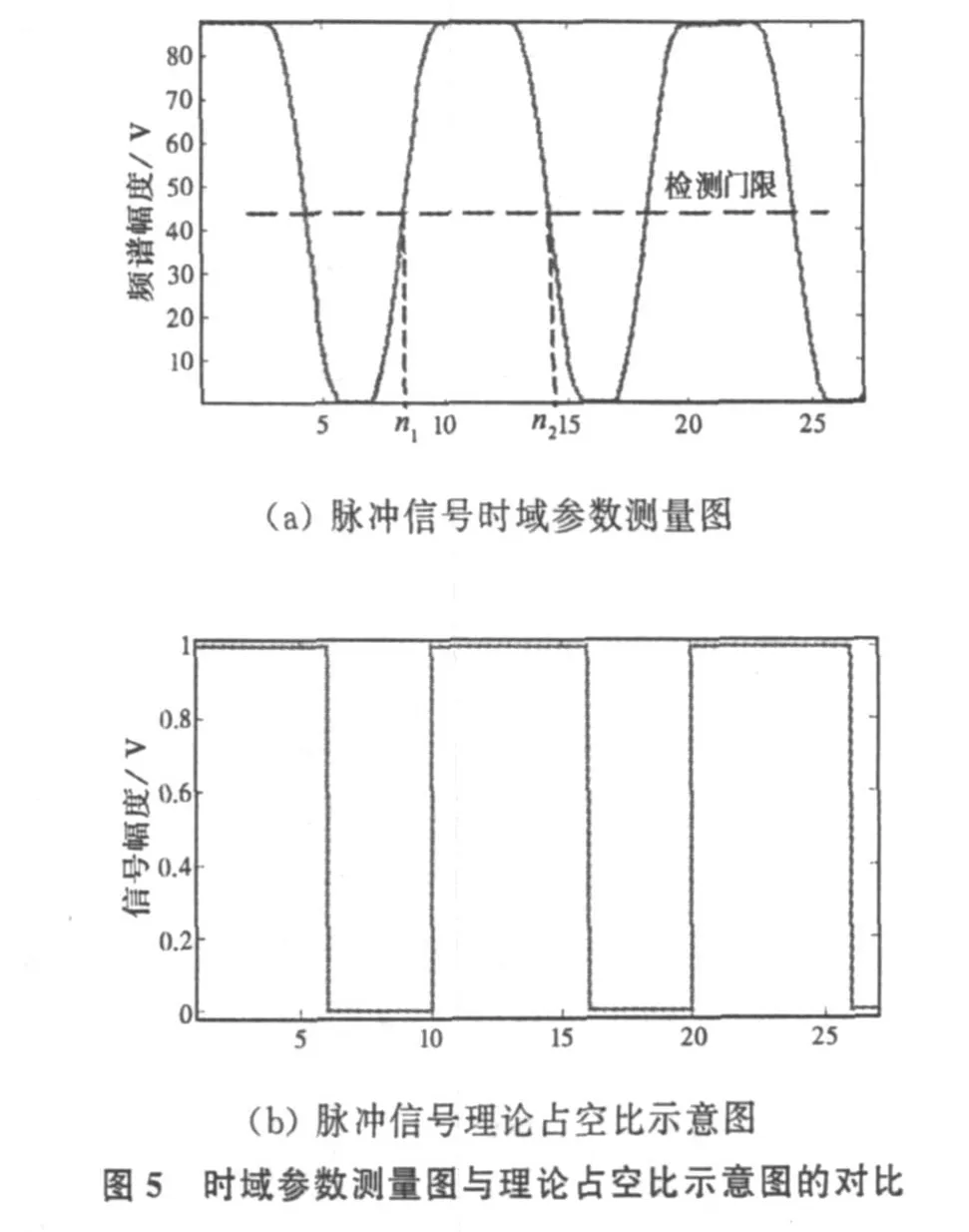
当工作参数f0=30.8 MHz;N=350;而各通路数据帧起始时刻按照式(5)和式(6)设置,其中d=1(数据帧逐点滑移),n0=0时,得到载频 f 0=30.8 MHz的脉冲信号时域参数测量图,如图5(a),图5(b)为该脉冲信号理论占空比示意图。

当窗宽N小于脉内(或时限信号持续时间内)有效采样点数时,图5(a)形状为等腰梯形的脉冲串,通常取脉顶频谱幅度平均值的一半作为检测门限,统计某单个等腰梯形脉冲首次高于和首次低于检测门限的时刻n1,n2。由于递归算法公式中采用左对齐方式加窗,因此,由式(8)计算该脉冲的起始时刻n r,终止时刻n f和脉宽 n w。

因为信号在频域具有能量集中的特性[9],递归算法采用频域数据来测量时域参数,相比用时域数据测量时域参数,抗噪性能加强了,提高了检测灵敏度。

3.3 参数N的设置与调整——影响时间分辨率、频率分辨率、抗噪性能

虽然通过对频谱细化系数α和数据帧的滑移量d的调整,可以使时频网格的频域间隔Δf grid和时域间隔Δtgrid达到很小,但是并不意味着频率分辨率Δf(指能够区分频率轴上靠得很近的两信号或两频率分量的最小频率间隔)或时域分辨率Δt(指能够区分时间轴上靠得很近的两信号或时限信号的起始时刻、终止时刻的最小时间间隔)的改善。

递归运算的频率分辨率Δf和时间分辨率 Δt受采样频率f s、窗口宽度N(等于循环迭代次数)、窗函数形状等因素的影响[7]。Δf正比于f s/N,Δt反比于fs/N。N变大,频域分辨率提高,而时域分辨率下降,二者仍然受制于“测不准原理”。但在一定的范围内,对循环迭代次数 N的调整,使得递归运算具有了可调可控的时间分辨率、频率分辨率。

假设有一个分段正弦信号

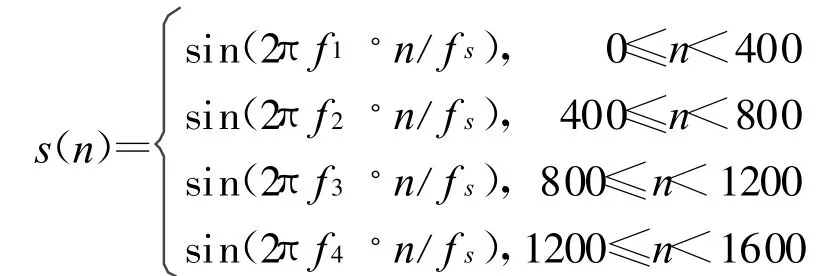
其中:f 1=52 Hz,f 2=54 Hz,f 3=56 Hz,f 4=58 Hz,f s=200 Hz。当工作参数 f m=(50+0.01m)(Hz),m=0,1,…,99;d=10;N 分别取 100、200和400时,利用递归算法得到的结果,如图6。通过对比可以看到,N较小时,具有较好的时间分辨率,而相应的频率分辨率则不高,随着N的增加,频率分辨率变得越高,但此时的时间分辨率则会相应地下降。

另外,由图6还可以看到,参数 N除了影响时、频分辨率外,还影响着谱线的幅度。N越大,谱线的幅度越大,则系统的抗噪性能越好。

4.结 论

递归算法具有很大的灵活性,非常适合对局部频段实时地进行频域参数测量、时域参数测量和二维时频谱分析,三项任务可独立完成,也可相互配合完成。时频分析系统需要根据某种规则做出工作参数的设置与调整,使其在保证实时性,时间分辨率,频率分辨率,时、频参数测量精度,抗噪性能等性能指标时统筹调度通路资源,协调工作。

[1] 李岳霖,庞伟正,等.多普勒雷达测量轻武器弹丸转速方法研究[J].电波科学学报,2007,22(3):502-507.

LI Yuelin,PANG Weizheng,et al.Measuring method of rotation velocity for small arms projectiles by Doppler radar[J].Chinese Journal of Radio Science,2007,22(3):502-507.(in Chinese)

[2] 袁伟明,王 敏,吴顺君.一种新的 LPI信号的截获方法[J].电波科学学报,2005,20(1):73-76.

YUAN Weiming,WANG Min,WU Shunjun.A novel interception of LPI signals[J].Chinese Journal of Radio Science,2005,20(1):73-76.(in Chinese)

[3] 徐玉清,郎 锐,高 攀.基于小波的信息保持型雷场图像融合算法[J].电波科学学报,2009,24(2):233-237.

XU Yuqing,LANG Rui,GAO Pan.Wavelet-based information restorefusion method of landmine field images[J].Chinese Journal of Radio Science,2009,24(2):233-237.(in Chinese)

[4] 王小龙.DFT和交替DFT调制滤波器组设计算法研究[D].陕西西安:西安电子科技大学,2008.

[5] JACOBSEN E,LYONS R.The sliding DFT[J].IEEE Signal Processing Magazine,2003,20(3):74-80.

[6] 黄寒华.滑动DFT算法研究[D].江苏南京:东南大学,2006.

[7] DRESSLER K.Sinusoidal extraction using an efficient implementation of a multi-resolution FFT[C]∥Proc.of the 9th Int.Conference on Digital Audio Effects,Montreal,Canada,September 18-20,2006.

[8] FARHANG-BOROUJENY B,GAZORS.Generalized sliding FFT and its application to implementation of block LMS adaptive filters[J].IEEE Transactions on Signal Processing,1994,42(3):532-538.

[9] 刘 平,靳成英,陈曾平.一种基于短时FFT的宽带数字接收机设计[J].信号处理,2008,24(6):988-991.

LIU Ping,JIN Chengying,CHEN Zengping.A shorttime FFT based design for wideband digital reconnaissance receiver[J].Signal Processing,2008,24(6):988-991.(in Chinese)