战场电磁信号环境最复杂原理预测

陈行勇 张殿宗 王 祎 肖昌达 陈海坚

(1.92493部队博士后科研工作站,河北秦皇岛066001;2.91404部队,河北秦皇岛066001)

1.引 言

战场电磁信号环境定量分析是认识和理解战场电磁环境本质规律的需要,可以为雷达信号分选和识别、战场电磁环境构建、控制和评估提供技术支持。近年来,战场电磁环境复杂度评估已经成为电子对抗领域的研究热点[1-6]。作为系统科学新的分支,组成论[7]通过广义集合、分布函数和复杂程度三个概念分析事物组成,为存在组成问题的客观事物提供了统一的认识模型、分析工具、计算方法和原理,对于客观事物的复杂程度给出了普遍的精确化定义,并揭示了有随机性的事物都遵守最复杂原理[7]。组成论指出复杂程度如质量、能量一样是客观事物自身具有的客观物理量,每个具体的客观事物都有明确的复杂程度,这为复杂性研究提供了一条康庄大道。作为客观事物,由于谐波分量、信号样式和辐射源等都是由不同的因素组成,并且在时域、空域、频域和能域的分布状态存在差异,战场电磁信号环境显然存在组成问题,可以使用组成论的概念、模型和原理进行研究。至今未见将系统论的思想和方法应用于战场电磁环境复杂性研究的报道。

雷达信号分选在雷达信号处理中占有很重要的作用[8-9]。国内有研究人员将熵的概念用于信号分选、聚类和识别[10-12],但是利用熵和复杂程度的概念进行战场电磁环境定量分析很少。例如,文献[13]认为脉冲密度不是电磁信号环境复杂程度合适的度量值,引入类型熵和密度熵作为电磁环境复杂性测度,探讨了电磁信号环境熵度量。文献[14]针对跳频信号的侦察、分选,提出了“复合信息熵”的定量评估指标,该指标综合考虑电磁环境中的信号类型数、跳频信号数目、跳速和信道分布情况。

现代战场电磁辐射源的多元化是电磁环境复杂化的根本原因。电磁环境的复杂性表现在电磁波传播在空域上的交错、电磁辐射行为在时域上的集中、电磁辐射信号载频在频域上的拥挤和电磁辐射强度在能域上的起伏。每一域的电磁辐射活动情况都分别从不同方面表现出电磁环境的复杂。由于电磁波的交叉传播,才使得同一时间内,空间中的任一点上能够同时接收到众多信号,这些信号的频谱分布具有足够的随机性,同时战场电磁兼容又为这种随机性提供了限制条件。这为使用最复杂原理分析其频谱分布规律提供了理论依据。

利用组成论分析战场电磁信号的组成,通过定义电磁信号时间、频谱和空间分布状态的复杂程度,在战场电磁信号环境具有足够的随机性的条件下,利用最复杂原理和战场电磁兼容的约束条件,预测电磁信号频谱宽度分布规律,并进行了仿真计算。

2.战场电磁信号环境频谱分布预测

2.1 复杂程度的概念

根据组成论,对于一个广义集合[7],由于其个体总个数N是确定值,而标志值为x的个体个数n是x的函数,所以n/N也是x的函数,则广义集合的内部状态的离散变量复杂程度为

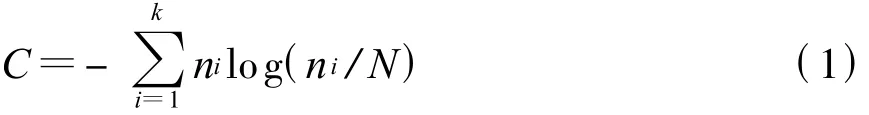
式中:k表示广义集合内的不同的标志值的个数;ni表示每种标志值占有的个体的数量。

设g(x)表示广义集合的密度分布函数,f(x)表示相对密度分布函数,即标志值 x有单位增量时个体个数的增量。则广义集合的内部状态的连续变量复杂程度为

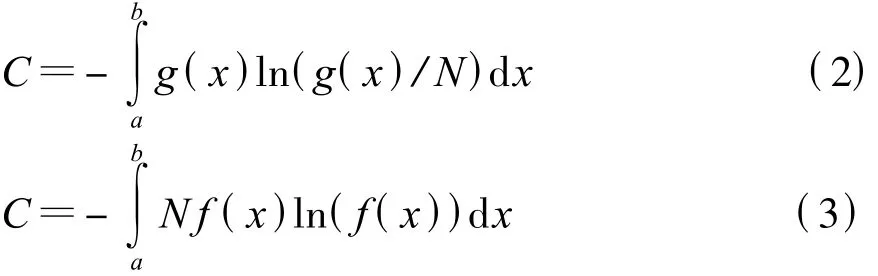
组成论指出,一个广义集合内的各个个体的特征(标志值)差别越大,复杂程度值C就越大。而各个个体的特征(标志值)完全相同(清一色,没有差别)则C为零。复杂程度是广义集合分布函数的泛函数。客观事物都有复杂程度值,且复杂程度没有负值。

2.2 电磁信号环境复杂程度

将战场电磁信号全体视为一广义集合,各电磁信号在时间持续长度、频谱占用宽度和空间体积大小方面存在差异,因此,按照组成论,战场电磁信号环境具有明确的复杂程度量。设在时间[t1,t2]内,频率[f 1,f 2]内,空间VΩ内,战场电磁信号源总数为N。战场电磁信号关于时间宽度t的相对分布函数为st(t),st(t)即为时间占有宽度为t的战场电磁信号占信号总数的比例;战场电磁信号关于频谱宽度f的相对分布函数为s f(f),sf(f)即为频谱宽度为f的战场电磁信号占信号总数的比例;可以被感知的战场电磁信号关于空间体积v的相对分布函数为(v),(v)即为占有空间体积为v的战场电磁信号占信号总数的比例。

2.2.1 时间宽度分布复杂程度

定义战场电磁信号环境的时间宽度分布复杂程度为

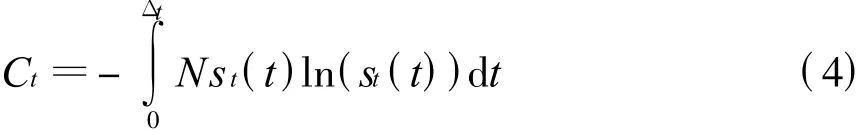
2.2.2 空间体积分布复杂程度

定义战场电磁信号环境的空间体积分布复杂程度为

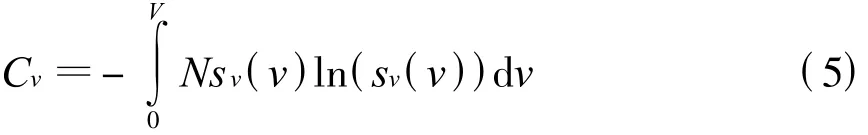
式中:V为战场空间体积;Cv描述了战场电磁信号环境关于占有空间体积大小差异的丰富程度。

2.2.3 频谱宽度分布复杂程度

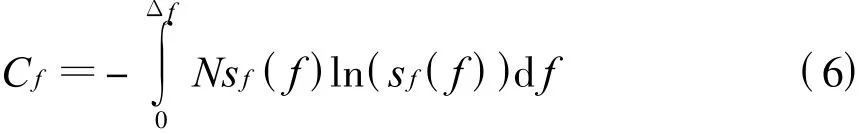
定义战场电磁信号环境的频谱宽度分布复杂程度为式中,Δf=f2-f1。Cf描述了战场电磁信号环境关于频谱宽度差异的丰富程度。

2.3 基于最复杂原理的频谱宽度分布函数预测

2.3.1 战场电磁频谱分割

由于每个广义集合都有一个明确的分布函数,寻找和获得分布函数就意味着发现了一类现象背后隐藏的规律,所以,每当把某些客观事物归结为广义集合以后的一个重要目标就是找出该广义集合的分布函数。对于有随机性的广义集合,由于它服从最复杂原理,这就提出了一个新的普遍适用的思路:利用最复杂原理从理论上求解广义集合的分布函数。由于复杂程度是分布函数的泛函数,因此可以利用复杂程度(泛函数)最大,加上一定的约束条件,求得广义集合的分布函数。

战场电磁信号占有频谱宽度分布可以抽象为“斩乱麻”[7]问题。战场电磁兼容要求在同一战场电磁环境下,己方各种作战装备能够执行各自的作战功能,并且不降低战技指标。在同一战场电磁环境下的作战装备包括双方的作战装备,战场电磁兼容往往是针对作战的己方而言的,作战双方的电磁兼容是绝对不可能实现的。从电子对抗方面来说,作战时一方的目标,就是最大限度地让己方的干扰设备与对方的信息化装备不兼容。对于己方接收的对方电磁信号来说,战场电磁兼容的要求使得电磁信号的频谱具有不交叉分割占用的最大可能性,换一句话说,若接收到的对方电磁信号对频谱的分割占用具有足够的随机性,频谱宽度的长短就构成了其复杂性,则依据最复杂原理,电磁信号的频谱宽度分布状态具有最复杂的趋势。因此战场电磁信号对频谱的分割占用问题就是把战场电磁信号看成一个广义集合而寻找它关于频谱宽度的分布函数。

2.3.2 频谱宽度分布预测

在频谱宽度 f为连续变量的情况下,战场电磁信号频谱宽度的相对分布函数为sf(f)的含义是频谱宽度在 f到f+δf很小范围(δf为f的微元)的信号源占信号源总数N的百分比为sf(f)·δf,而它的复杂程度Cf应当是

式(7)表明复杂程度Cf是分布函数sf(f)的泛函,其最大值以及取最大值时的sf(f)可以利用拉格朗日方法求解。使用拉格朗日方法求解这个未知函数还要约束条件,频谱宽度之和一定提供了这个约束条件。所谓频谱占用就是把频谱分割成很多段,假设各信号频谱宽度的合计值等于 μΔf,若0≤μ＜1,则信号源必定存在未占用的频段,若μ＞1,则信号源必定存在共同占用的频段,若μ=1,则频谱恰好被无缝无交叉占用,或者未占用和共同占用的频段同时存在。根据分布函数的含义,显然有

即信号源集合的频谱宽度之和是各个信号源频段宽度与其占的百分比的乘积再乘以信号源总数N的积分。而各个信号源的百分比(sf(f)Δf)的积分(合计值)显然应当等于100%,即

式(8)和式(9)分别表示两个约束条件,其含义是各个信号源频谱宽度的总和与信号源频谱范围宽度的μ倍相等,各个信号源的数量的合计值与总的信号源数量相等。由拉格朗日法可知,求分布函数sf(f)需构造一个新的函数F

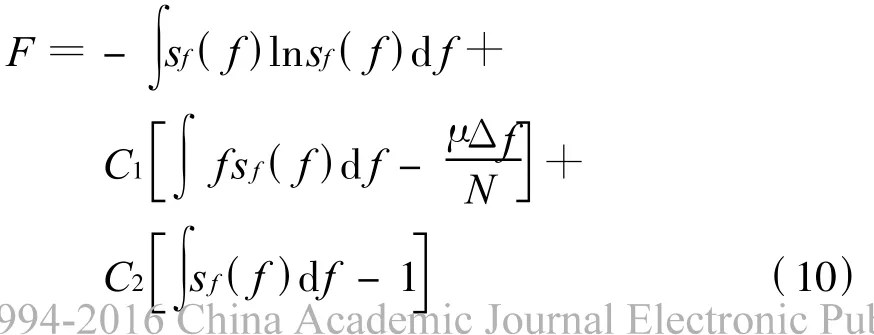
式中,C1和 C2是与 Δf,N,μ有关的常数。对式(10)求解,得到使复杂程度极大对应的分布函数为

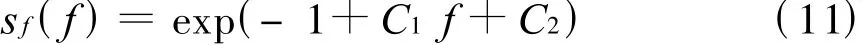
利用式(8)和(9)与式(11)联立可以消去未知常数 C1,C2。解得

注意到μΔf/N的含义是信号源频谱的平均宽度,以w 表示它,得到

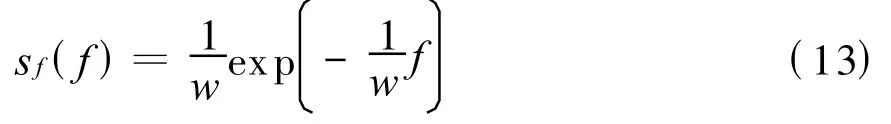
它是一个负指数分布函数。它显示频谱宽度 f窄的信号源多而频谱宽的信号源的数量依负指数关系而减少。

3.仿真计算和结果分析

3.1 仿真计算

假设有一段范围为[f 1,f 2],宽为Δf=f 2-f 1的频谱被足够多的N个战场电磁辐射源随机占有,并且假设对于0≤μ＜1,对应信号源有未占用的频段且无共同占用频段,对于μ＞1,对应信号源无未占用的频段且有共同占用频段,对于μ=1,对应频谱恰好被无缝无交叉占用,可以采用以下方法对电磁信号频谱宽度分布进行模拟。

1)在[0,1]范围内产生N-1个均匀分布随机数并乘以Δf后加f 1,与f 1和f 2一起由小到大构成一个N+1点序列x(m),x(m)服从[f 1,f 2]上的均匀分布,它们即是频谱占用的断点;

2)计算序列 x(m)的相邻数值的差,并乘以μ,得到的就是各个战场电磁辐射源占用的频谱宽度;

3)统计这些频谱宽度的分布,即统计分布在各个频谱宽度区间的辐射信号的数量占总数的百分比,得到战场电磁信号频谱宽度分布函数;

4)把统计得到的信号频谱宽度分布与理论预测进行比较,即将统计分布与预测得到的分布函数sf(f)=(1/w)·exp(-f/w)进行对比。

3.2 结果分析

取Δf=f 1=10 MHz,f 2=20 MHz,N=1000,图1示出了 μ=1,μ=1.2和 μ=0.8时实验得到的战场电磁信号频谱宽度分布与理论预测的对比。

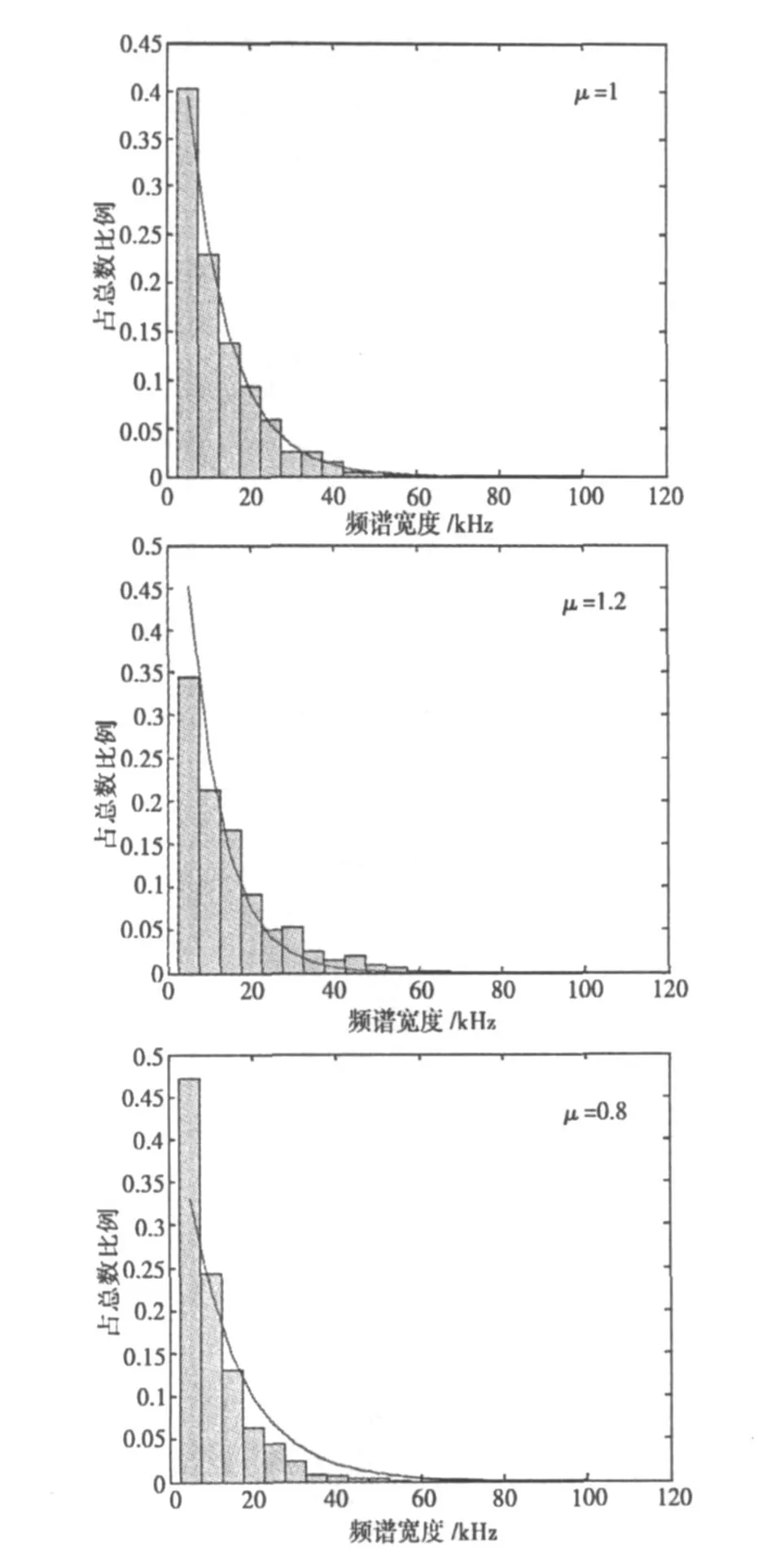
图1 战场电磁信号频谱宽度分布仿真与理论预测的对比

由图1可知,计算机模拟数据和理论计算吻合。战场电磁信号的数量随着其占有的频谱的宽度增加急剧减小,其变化规律服从负指数分布。这为我们理论预测战场电磁信号环境的频谱和带宽分布提供了理论依据,可以指导我们构建电子对抗训练复杂电磁环境,也可以为雷达信号分选、聚类、识别提供新的途径。

4.结 论

熵和复杂程度是信息论和系统科学的重要概念,然而熵原理(最复杂原理)在电子对抗领域却没有发挥应有的作用,这是我们应该重视的问题。从战场电磁信号环境的时间、空间和频率占用的差异来定义复杂程度,用最复杂原理预测战场电磁信号频谱宽度分布函数,不仅为客观定量分析战场电磁环境复杂性提供了新的途径,而且为复杂战场电磁环境下雷达、通信信号分选、聚类和识别提供了新的思路。本文既是熵与交叉科学研究的探索,也是为将熵原理推广到战场电磁环境分析所进行的初步尝试。

[1] CAI X F,SONG JS.Analysis of complexity in battlefield electromagnetic environment[C]//IEEE Conference on Industrial Electronics and Applications.Xi'An:IEEE,2009:2440-2442.

[2] JAEKEL B W.Electromagnetic environments-Phenomena,classification,compatibility and immunity levels[C]//Proceedings of The IEEE Region 8 Conference.St.Petersburg,Russia:IEEE,2009:1498-1502.

[3] XU J H,LIU G B,YU Z Y,et al.A meta-synthesis of evaluating battlefield electromagnetic environment effects[C]//International Conference on System Simulation and Scientific Computing.ChengDou:IEEE,2008:79-82.

[4] 陈行勇,张殿宗,王 祎,等.面向对象的战场电磁环境复杂度评估[J].电子对抗信息技术,2010,25(2):74-78.

CHEN Hangyong,ZHANG Dianzong,WANG Yi,et al.Object-oriented battlefield electromagnetic environment complexity evaluation[J].Electronic Information Warfare Technology,2010,25(2):74-78.(in Chinese)

[5] 代合鹏,苏东林.电磁环境复杂度定量分析方法研究[J].微波学报,2009,25(3):25-27.

DAI Hepeng,SU Donglin.Study of the complexity evaluation on electromagnetism environment[J].Journal of Microwaves,2009,25(3):25-27.(in Chinese)

[6] 邵国培,刘雅奇,何 俊.战场电磁环境的定量描述、模拟构建与复杂性评估[C]//中国电子学会电子对抗分会第十六届学术年会论文集.贵阳:中国电子学会电子对抗分会,2009:61-66.

[7] 张学文.组成论[M].合肥:中国科学技术大学出版社,2004:1-6.

[8] 朱 明,普运伟,金炜东,等.基于时频原子方法的雷达辐射源信号特征提取[J].电波科学学报,2007,22(3):458-462.

ZHU Ming,PU Yunwei,JIN Weidong,et al.Feature extraction of radar emitter signals based on time frequency atoms[J].Chinese Journal of Radio Science,2007,22(3):458-462.(in Chinese)

[9] 陶荣辉,李合生,韩 宇,等.基于直方图和小波网络的雷达信号识别方法[J].电波科学学报,2005,20(6):784-788.

TAO Ronghui,LI Hesheng,HAN Yu,et al.A novel algorithm of radar signal recognition based on histogram and wavelet networks[J].Chinese Journal of Radio Science,2005,20(6):784-788.(in Chinese)

[10] 孙盼杰,刘 刚,王 杰.基于PRI熵的雷达信号聚类方法研究[J].电子信息对抗技术,2008,23(1):22-25.

SUN Panjie,LIU Gang,WANG Jie.Approach to radar signal clustering based on PRI entropy[J].Eelectronic Information Warfare Technology,2008,23(1):22-25.(in Chinese)

[11] 张葛祥,胡来招,金炜东.基于熵特征的雷达辐射源信号识别[J].电波科学学报,2005,20(4):440-445.

ZHANG Gexiang,HU Laizhao,JIN Weidong.Radar emitter signal recognition based on entropy features[J].Chinese Journal of Radio Science,2005,20(4):440-445.(in Chinese)

[12] 国 强.复杂环境下未知雷达辐射源信号分选的理论研究[D].哈尔滨:哈尔滨工程大学,2007.

GUO Qiang.Intelligent recognition methods for radar emitter mignals[D].Harbin:Harbin Engineering U-niversity,2007.

[13] 李 峥.电磁信号环境的熵度量第十三届电子战新概念新理论新技术学术年会论文集[C]//成都:电子对抗国防科技重点实验室,2009:204-208.

[14] 陈利虎,张尔扬.一种新的定量评估电磁环境复杂度方法[J].电子对抗,2009,33(2):6-9.

CHEN Lihu,ZHANG Eryang.A new method for the quantificational evaluation of the complexity of electromagnetic environment[J].Electronic Warfare,2009,33(2):6-9.(in Chinese)