基于三角网格的凸导体目标SB-ILDC算法

朱宗宝 许小剑 隋 淼

(北京航空航天大学,北京 100191)

1.引 言

由于物理光学(PO)感应电流在目标的阴影边界以及深阴影区失效,在使用PO计算目标的双站雷达散射截面(RCS)时会产生明显误差。针对这个问题,Yaghjian和Shore等人先后提出了平面增量长度绕射系数(ILDC)[1]、光滑凸曲面阴影边界增量长度绕射系数(SB-ILDC)[2]、任意二维柱面 SBILDC[3]和三维物体 SB-ILDC[4]等方法,用来计算目标在阴影边界处由不一致电流(PO感应电流与真实感应电流的差值)产生的表面绕射场。其中,三维物体SB-ILDC已应用于采用曲面建模的Xpatch?中,从而显著改善了Xpatch?中PO方法的计算精度[5]。当目标采用参数样条曲面建模时,目标表面法矢和曲率半径可直接采用微分几何的解析方法进行计算,因而SB-ILDC可直接应用于参数样条曲面模型目标表面绕射场的计算。在RCS理论计算中,目标几何结构也常采用离散三角网格模型表示,这种网格模型采用多个平面三角形来拟合目标的曲面结构,无法使用微分几何解析方法来计算SB-ILDC所需的目标几何参数。

本文提出了一种基于三角网格模型的目标阴影边界曲线寻迹算法,并通过对目标阴影边界处的法矢和曲率半径的估算,将SB-ILDC推广应用于三角网格模型目标阴影边界处表面绕射场的计算。第二节详细讨论基于三角网格模型的目标阴影边界曲线寻迹算法;第三节结合文献推导结果,给出 SBILDC绕射场的计算方法;第四节通过对典型目标数值结果同Mie级数解比对,验证本文方法的正确性和有效性。

2.基于三角网格模型的目标阴影边界曲线寻迹算法

SB-ILDC的基本思路是:通过对PO散射场EPO引入一个绕射修正项ESB,以此改善PO法对目标散射场E S的计算精度,即

SB-ILDC之所以对PO具有修正作用,是因为在高频散射下,不一致电流对双站散射场的贡献在阴影边界附近十分明显,而远离边界后则迅速衰减。因此,采用SB-ILDC计算目标表面绕射场ESB时,首先需要对目标阴影边界寻迹。

当以三角网格模型来表示目标几何结构时,通过三角网格模型快速准确地计算出目标的阴影边界及相关参数,是将SB-ILDC应用于三角网格模型目标的关键。这是因为,目标阴影边界的位置决定了产生绕射场的不一致电流的相对相位,阴影边界处目标表面法矢和曲率半径决定了用于局部近似的二维圆柱的姿态和尺寸,两者直接影响绕射场ESB的计算精度。为此,本文提出一种基于三角网格模型的光滑凸表面目标阴影边界曲线寻迹算法,采用由面元表面直线段组成的折线近似表示阴影边界曲线,并利用节点插值估算阴影边界处的法矢及曲率半径,从而将阴影边界曲线寻迹方法从曲面模型[5]推广到更一般的平面三角网格模型。

对于凸表面目标上任意一点P,n^P为P点的表面法矢,k^inc为入射波矢。如果k^inc·＜0,表明P点在照亮区;如果k^inc·n^P＞0,表明P点在阴影区;如果k^inc·n^P=0,则表明P点在阴影边界曲线上。因此,对凸表面目标阴影边界寻迹就是要找到令k^inc·n^P=0的P点集合。因此,对光滑凸表面目标阴影边界曲线寻迹的具体步骤如下。

步骤1:计算各节点处表面法矢

由于三角网格模型采用多个平面三角形近似表示目标表面的曲面结构,通常只能计算节点处的法矢,其他各点处的法矢需要采用插值的方法进行估算。为此,首先采用力学平衡法计算目标模型各个节点处的法矢[6]

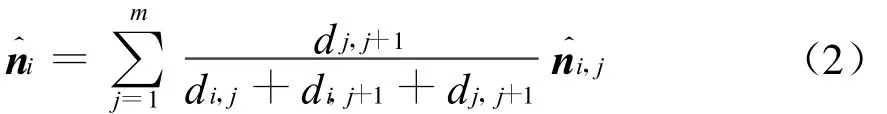
式中:n^i为节点i的表面法矢;m为节点i的邻面个数;n^i,j为节点i第j个邻面的表面法矢;d i,j、d i,j+1和d j,j+1分别为第j个邻面内节点i的两个邻边和对边的边长。

步骤2:判断面元上存在阴影边界与否

遍历目标上所有的面元,用k^inc分别点乘面元三个节点的法矢。对于某一个面元,如果三个节点·的计算值同时为正或为负,则该面元在阴影区或照亮区,否则该面元上存在阴影边界曲线。

步骤3:确定面元上的阴影边界线段

对所有存在阴影边界曲线的面元,采用线性插值的方法计算阴影边界曲线、表面法矢及曲率半径。可分为以下三种情形,如图1所示。

图1 三角网格曲面阴影边界计算示意图

第1种情形:对于三个节点k^inc·n^都不为零的面元,增量长度的阴影边界线段的两个端点将位于·正负相异两个节点之间的边上。若这两个节点记为A和B,坐标为r A和r B,法矢为n^A和n^B,则线段AB上的任意一点P的单位法矢可表示为

若令P点为所求线段的一个端点,即 k^inc·n^P=0,则线性插值参数t为

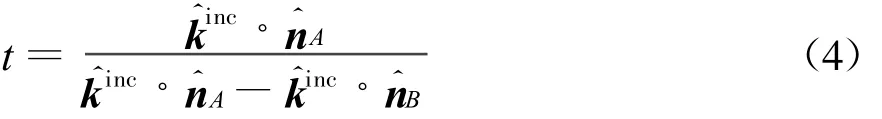
线段端点P的坐标为

同理,对于同一个面元上另外一对k^inc·n^正负相异的两个节点,可以类似地得到增量长度阴影边界线段的另外一个端点。

第2种情形:对于仅有一个节点k^inc·n^=0的面元,则这个节点就是所求增量长度阴影边界线段的一个端点,另外一个端点可以通过同上面类似的方法计算。

第3种情形:对于有两个节点k^inc·n^=0的面元,则这两个节点就是所求增量长度阴影边界线段的两个端点。

步骤4:形成阴影边界

按照步骤3中方法,求出所有含有阴影边界面元上的阴影边界线段,并将其依次连接,就得到了三角网格模型光滑凸表面目标完整的阴影边界曲线。

根据上述步骤1～4,本文算法在计算目标阴影边界时仅需遍历一次面元,所消耗的时间复杂度为o(N)(N为面元数)。可见,采用 SB-ILDC修正PO双站散射场不会显著增加计算时间。由于本文采用分段折线近似地表示阴影边界曲线,在三角网格足够精细的情况下(例如网格边长为～),这种近似可以满足工程计算的精度要求。

此外还应指出,采用本文的寻迹算法可以一次计算多条阴影边界曲线,从而提高计算效率。

3.三维目标SB-ILDC绕射场计算

在计算三维目标SB-ILDC绕射场ESB时,需要逐段地计算增量长度阴影边界产生的绕射场d ESB,而目标表面沿着入射波方向的一个表面条带所产生的绕射场d ESB可以近似地用二维圆柱条带产生的绕射场来代替。首先建立增量长度二维圆柱阴影边界处的局部坐标系,如图2所示。

图2 二维圆柱局部坐标系

在图2中,kinc为入射波矢,k^inc为kinc的单位矢量,k为波数,kinc=k k^inc;PSB为阴影边界上的一点,n^SB为PSB点处的表面法矢;(x^l,y^l,z^l)为以PSB为原点的局部直角坐标系,y^l轴指向为P SB处n^SB方向,z^l轴指向为P SB处阴影边界曲线切线方向,并且满足k^inc·x^l＞0;(θol,φol)和(θl,φl)分别为 kinc和散射方向rl的俯仰角和方位角。因为对于 PSB点有k^inc·n^SB=0,即k^inc在 x l-z l平面内,故 φol=π。

增量长度二维圆柱的阴影边界绕射场可表示为

式中:ETMol和ETEol分别为入射电场Einc在PSB处的TM和TE分量;d E TM和d E TE分别为P SB处增量绕射场d ESB的TM分量和TE分量。

设全局坐标系原点处入射电场为E0,则P SB处入射电场Einc(P SB)可表示为

则式(6)中ETMol和ETEol可分别表示为

根据文献[4]的推导,并考虑本文采用 ejωt作为时间因子,式(6)中d E TM和d E TE可分别表示为

式中:

式(10)和式(11)中FSBz和GSBz分别为二维圆柱SB-ILDC的增量绕射场的 TM和TE分量,具体表达式参见文献[2]。

得到三维目标所有的增量长度阴影边界的绕射场d ESB后,沿着阴影边界对d ESB积分,即可得到三维目标阴影边界处的绕射场ESB

式中,LSB为目标阴影边界曲线。

4.数值结果

本节给出几个将SB-ILDC应用于三角网格模型的算例,并对目标双站散射的计算精度进行分析。

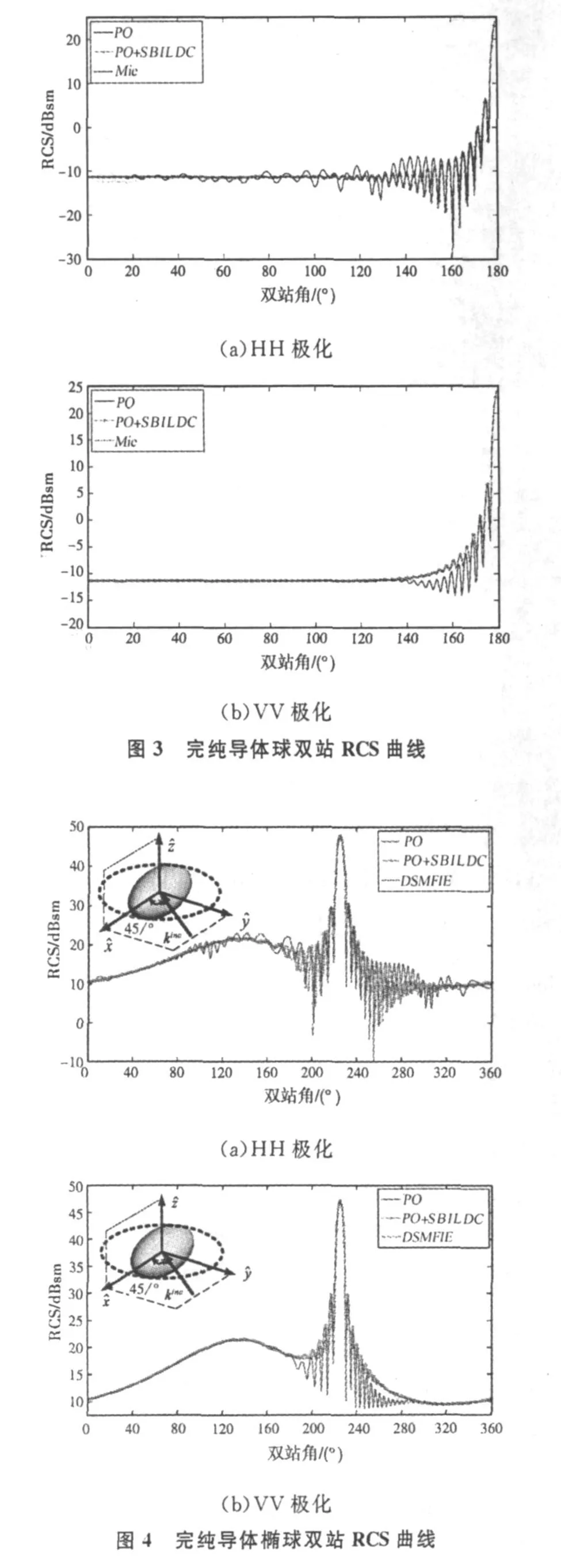
第一个算例为完纯导体球的双站散射。取ka=60(a为球半径);双站角从 0°到 180°变化,角度步进间隔为0.5°。图3(a)和(b)分别给出了水平(HH)极化和垂直(VV)极化下,采用PO、PO+SBILDC及Mie级数解计算得到的 RCS随双站角变化曲线。从图中可见,两种极化尤其是在双站角比较大的情况下,SB-ILDC对PO均有明显的改善。

第二个算例为完纯导体椭球的双站散射。取ka=50,kb=25(a,b分别为长轴和短轴半径);入射场俯仰角为0°,方位角为45°;散射方向俯仰角为0°,方位角从 0°到 360°变化 ,角度步进间隔为 0.5°。图4(a)和(b)分别给出了HH极化和VV极化下,采用 PO、PO+SB-ILDC及双面磁场积分方程(DSMFIE)[8]计算得到的RCS随双站角变化曲线。从图中可见,对于表面曲率连续变化的三维目标,SB-ILDC对PO的双站RCS同样具有明显的修正作用。

为了研究在各个双站角下SB-ILDC对PO是如何修正的,本文研究了导体球的一维距离像随双站角的变化特性,如图5所示。图5(a)和(b)分别给出了HH和VV极化的计算结果。计算参数如下:导体球半径a=0.1524 m;中心频率22 GHz,带宽 30 GHz;双站角 0°到 180°,角度步进间隔1°。以图5(a)为例,图中从左到右、从上到下依次给出了PO、SB-ILDC、PO+SB-ILDC和Mie级数解的结果。PO计算结果中第一条线迹表示镜面反射中心随双站角的变化,中间两条线迹表示由于PO电流在阴影边界处截断所引起的虚假散射中心随双站角的变化。对比Mie的结果可以看出,PO很好地计算了镜面反射对散射场的贡献,但是在阴影边界处引入了虚假的强散射回波,并且未计入爬行波对散射场的贡献。SB-ILDC则在阴影边界处修正了PO所引入的两个虚假散射峰,并且部分计入了爬行波对双站散射场的贡献。

注意到为了清晰地表示出各散射中心的变化特性,图中的色标范围均取为160 dB。因此,尽管在PO+SB-ILDC的结果中虚假峰仍然依稀可见,但这并不意味着SB-ILDC的修正效果差,事实上这些伪峰的值均在-80 dBsm以下,即便同爬行波比也属小值。

5.结 论

针对三角网格模型表示的光滑凸表面目标,研究了SB-ILDC对PO双站散射场计算的修正问题。提出了一种基于平面三角网格模型的目标阴影边界寻迹算法,推广了SB-ILDC的适用范围,并通过具体算例分析了SB-ILDC绕射场对目标随双站角变化的一维距离像的修正作用。数值结果表明:本文提出的阴影边界寻迹算法,可以用于三角网格光滑凸表面电大尺寸目标SB-ILDC绕射场计算。

[1] SHORE R A,YAGHJIAN A D.Incremental diffraction coefficients for planar surfaces[J].IEEE Trans.on Antennas Propagat.,1988,36(1):55-70.

[2] SHORE R A,YAGHJIAN A D,WOODWORTH M B.Shadow boundary incremental length diffraction coefficients for perfectly conducting smooth,convex surfaces[J].Radio Sci.,1997,31(6):1681-1695.

[3] YAGHJIAN A D.Incremental length diffraction coefficients for arbitrary cylindrical scatters[J].IEEE Trans.on Antennas Propagat.,2001,49(7):1025-1032.

[4] SHORE R A,YAGHJIAN A D.Shadow Boundary incremental length dif fraction coefficients applied to scattering from 3-D bodies[J].IEEE Trans.on Antennas Propagat.,2001,49(2):200-210.

[5] MOOREJ T.High order electromagnetic modeling for high f requency[R].Science Applications International Corporation,Champaign,IL,2004(AD-A706724).

[6] 柯映林.散乱数据几何造型技术及其应用研究[D].南京:南京航空航天大学,1992.

[7] WELCH W,WITKIN A.Free-form shape design using triangulated surfaces[J].In:SIGGRAPH 94 ConferenceProceedings,1994:247-256.

[8] SHORE R A,YAGHJIAN A D.Dual-surfaceintegral equations in electromagnetic scattering[J].IEEE Trans.on Antennas Propagat.,2005,53(5):1706-1709.