基于有限元概率设计的结构敏感性分析研究

文方针

(广东省公路勘察规划设计院,广东广州510510)

敏感性分析主要研究可靠度模型中各随机变量或其参数变化情况下对失效概率或可靠度指标的影响规律,它可用来提供各随机变量或其参数之间重要性程度的横向对比。对基于有限元的概率设计(ANSYS Probabilistic Design System)、结构优化和结构可靠度的校验十分重要,还可以对工程分析中的数据提出精度上的要求。如果可靠指标对某一随机变量的敏感性较高,则要求所提供的统计数据要相对精确,如果对某一随机变量的敏感性较低,则可以相对放松对统计数据的要求[1-5]。

通过层次分析获得影响结构可靠度的主要因素后,有必要进一步定量分析这些因素对可靠度影响的重要性。输入变量的重要性一般通过敏感性指标来度量。对于敏感性指标,目前尚无统一的标准,赵国藩[5]定义了无量纲敏感性指标,然后基于结构可靠度分析的一次二阶矩方法,推导了可靠指标对随机变量统计参数的敏感性公式。秦权[6]定义了随机变量的重要性敏感性指标、失效概率对随机变量均值敏感性指标、失效概率对方差敏感性指标。这些指标分别反映了随机变量及其均值、标准差对失效概率的影响程度。

在实际工程问题中,通常关心两类敏感性问题。其一,对于某一输出变量,对其输出结果影响最大(灵敏度最大)的输入变量有哪些。其二,对于某一输入变量,它的变化程度对于结构体系可靠度的影响。针对这两个方面,本文提出了两类敏感性概念及其具体的计算实施方法。

1 两类敏感性概念

1.1 第一类敏感性问题

第一类敏感性问题:对于某一输出变量 yi,设对其输出结果有影响的基本随机变量为为输入随机变量 x1的期望值,则对于该输出变量yi,可定义其敏感性向量为:,将该向量归一化后,可用敏感性饼图表示。

1.2 第二类敏感性问题

第二类敏感性问题:在实际工程问题中,结构尺寸、材料特性等均在均值附近波动,大多数随机变量的概率密度函数可由均值和均方差决定。因此,要研究各因素对结构失效的影响,只要研究其均值、均方差对结构的影响就足够了[7]。

对于复杂结构系统,设影响结构可靠度的因素x1,x2,…,xn是服从一定分布的随机变量,其均值、方差的一般表达式为Exi,Sxi,具体数值为

由三级工作模式[8],结构的系统可靠性可由以下可靠性向量来表示

式中:s为结构的可靠概率;Pd为结构的中介概率;Pf为结构的失效概率。定义随机变量xi对结构失效的无量纲敏感性矩阵为

求上述敏感性矩阵需获得Pf,Pd,Exi及Sxi的具体函数表达式。对于复杂结构体系,获得这些表达式是困难的。但是,获得大量离散样本是可以做到的。用增量代替偏导数,考虑到失效概率与损伤概率均很小,且 β(t)=Φ(Pf(t))[9,10],可用可靠度指标β代替概率P,将第二类敏感性定义为如下无量纲矩阵

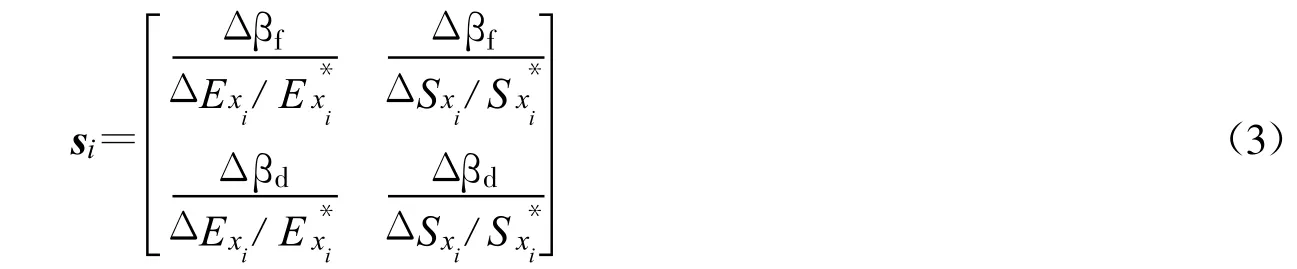
根据式(3),若将 Exi及Sxi在及附近波动,计算相应的βf,βd则可得到一系列的三维样本点,由这些样本点可拟合随机变量xi的敏感性曲面。这一敏感性曲面反映某一随机变量xi对结构可靠性的影响。将其在β0Exi坐标平面及β0Sxi坐标平面内投影得到曲线,求某一计算点处相应的斜率可获得该点处第二类敏感性无量纲矩阵。这一方法结果直观、便于应用,具有兼容性与实用性。

2 ANSYS PDS技术

2.1 ANSYS PDS数据流模型

结构可靠性分析中的敏感性问题其核心仍是有限元计算问题[11,12],考虑实际工程中的不确定因素,有限元分析的任何一个方面或输入数值都是一个离散性的分布参数,即某种程度上都是具有不确定性的。为研究不确定因素对结构可靠性指标的影响,必须将有限元分析技术与概率设计技术相结合,这就是基于有限元的概率设计,即ANSYS PDS(ANSYS Probabilistic Design System)。ANSYS PDS过程数据流程见图1。

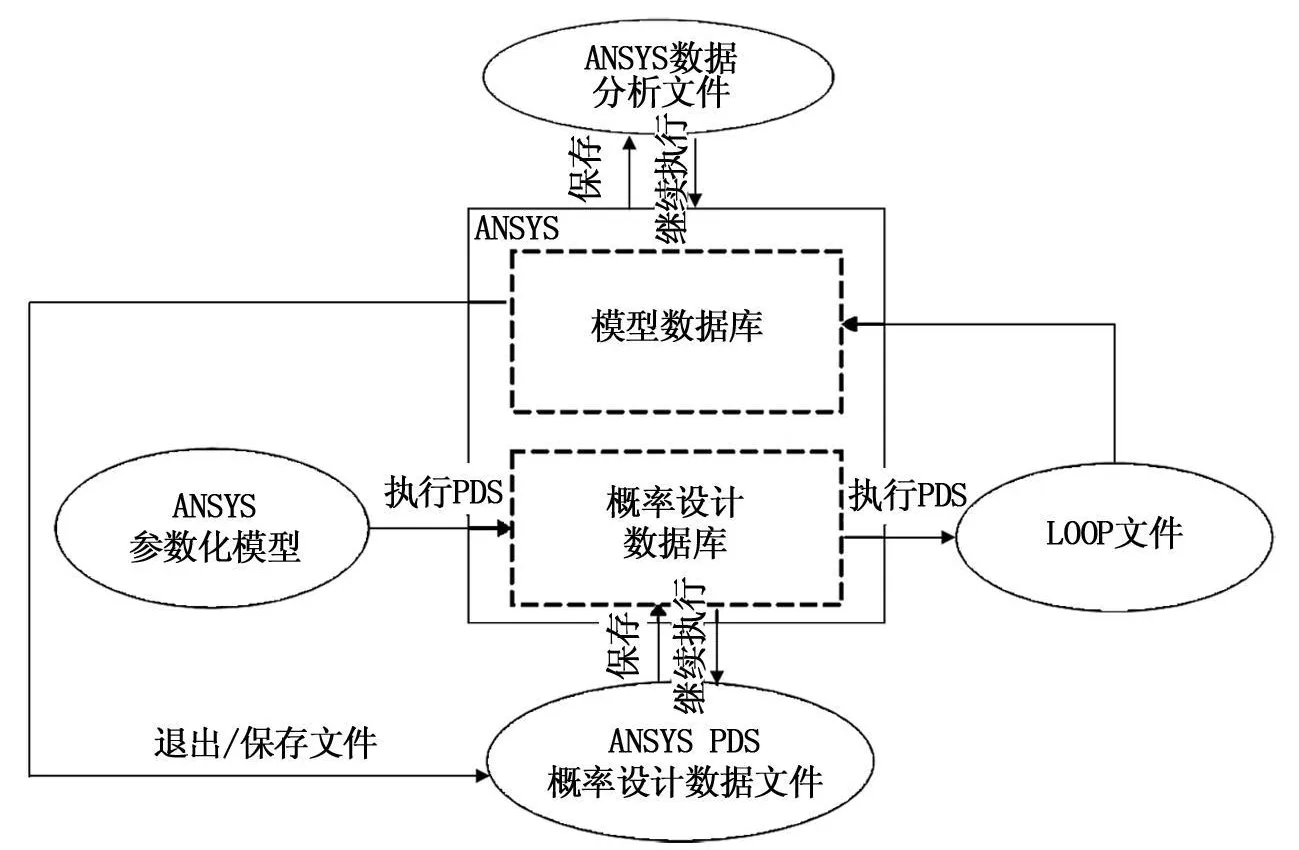
图1 ANSYS PDS过程数据流模型

2.2 ANSYS PDS基本过程

ANSYS基于有限元的概率设计分析的过程主要包括以下步骤。

(1)创建概率设计中需要的分析文件,分析文件必须包含完整的仿真分析过程。包括参数化有限元建模、求解、设置随机输入参数和随机输出参数。

(2)在ANSYS环境中执行分析文件包括命令流,初始化概率设计,建立概率设计的有限元分析数据库和所有参数。

(3)进入PDS处理器并指定所用的分析文件。

(4)定义随机输入参数。检查随机输入参数,可选项。定义随机输入参数间的相关性。

(5)定义随机输出参数。

(6)选择概率设计工具或方法。

(7)执行概率设计分析指定的仿真循环。

(8)读取并分析ANSYS PDS结果。

3 算例

3.1 工程背景

某桥于1998年2月竣工通车。主桥采用3跨连续下承式无风撑钢管混凝土系杆拱结构,跨径组合为55 m+83.6 m+55 m,桥宽25 m。

3.2 三维仿真模型

该桥于1998年、2000年及2003年进行了3次实桥试验。根据实测几何形态参数、裂缝分布、基础结构性能及基频模态对三维有限元模型进行了修正。全桥有限元模型共计单元2 528个,节点1 780个,见图2。本例对该桥主拱及边拱结构体系进行可靠度分析。

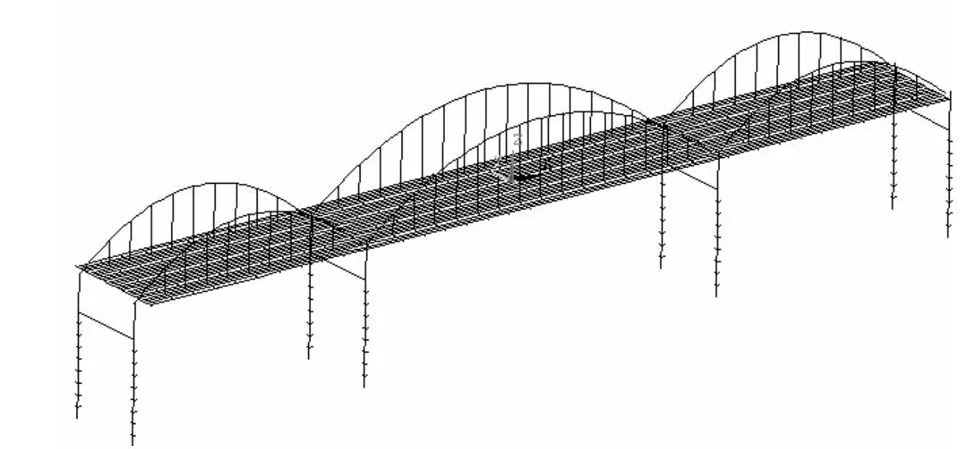
图2 三维有限元模型

3.3 敏感性分析

3.3.1 第一类敏感性分析

基于有限元模型采用Monte Carlo法进行分析,所有输入变量取值同时变化,考虑输出变量之间的相互作用,从而避免了确定性敏感性分析可能导致的错误,确定性敏感性分析的不足之处主要在于确定性分析采用的是典型的有限差分法(变化其中一个参数,同时其余各参数保持不变),忽略了输入变量之间的相互影响和作用。算例桥中跨最大轴力敏感性饼图和边跨最大轴力敏感性饼图见图3、4。

根据层次分析确定该桥基本随机变量按可靠度因子权重由大到小依次为:车辆活载(因子权重:0.333 674 528)、人行活载(因子权重:0.333 674 528)、边跨钢管混凝土弹性模量(因子权重:0.125 293 12)、中跨钢管混凝土弹性模量(因子权重:0.125 293 12)、温度作用(因子权重:0.118 947 208)、恒载效应(因子权重:0.080 620 44)、基础冲刷(因子权重:0.069 032 238)。输出量为边跨最大轴力、边跨最大挠度、中跨最大轴力和中跨最大挠度。根据第一类敏感性的定义,计算其中跨及边跨最大轴力敏感性饼图如图3、4所示。由敏感性饼图可知,对于边跨,对其轴力有重要影响的因素依次为活载、边跨钢管混凝土组合材料弹性模量、恒载。对于中跨,对其轴力有重要影响的因素依次为活载、恒载及温度。相对于中跨,边跨会发生较大的纵向位移,故材料弹性模量对边跨轴力会产生较大影响;而对于中跨,由于其位移较小,此时温度效应会在其上产生较大的次内力,影响其轴力。而材料弹性模量的影响则降为次要地位。这一结论与算例桥的力学特性是相符合的。且敏感性饼图的结果与层次分析法的结果也是一致的。这也验证了层次分析法的正确性。

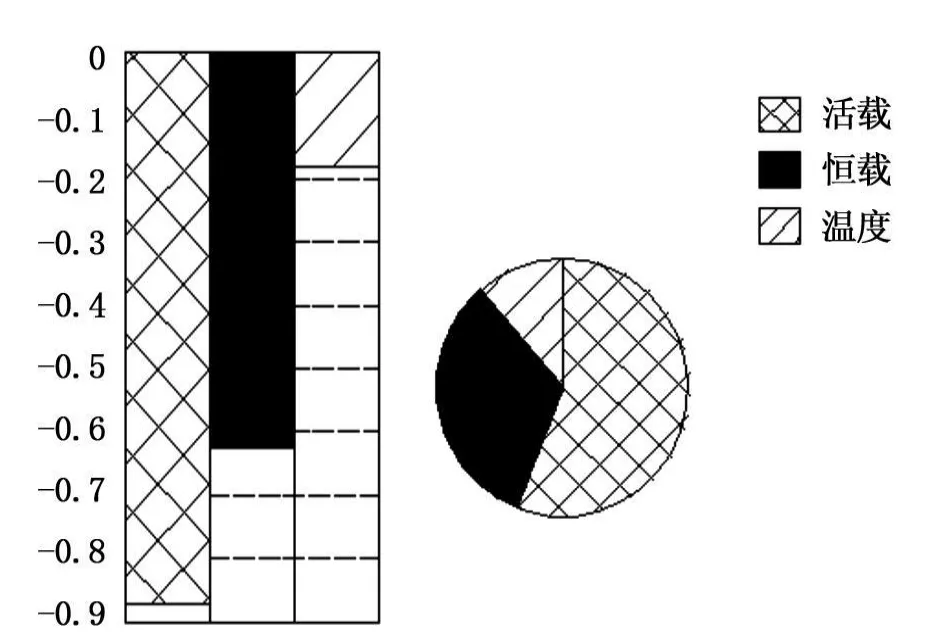
图3 中跨最大轴力敏感性饼图

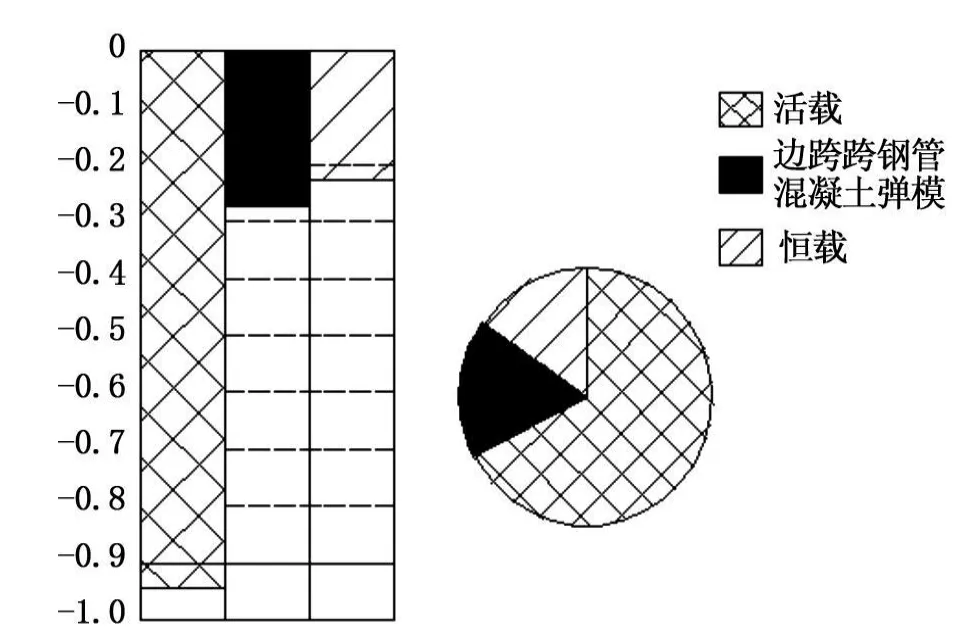
图4 边跨最大轴力敏感性饼图

3.3.2 第二类敏感性分析

对于算例桥,为研究弹性模量的变化对失效概率影响,使弹性模量期望值Exi在40.6～45.3 G之间变化,弹性模量均方差Sxi在0～100 G之间变化。由此计算结构相应的可靠度 βf。可拟合获得钢管混凝土弹性模量期望值-均方差-可靠度指标曲面,即钢管混凝土弹性模量曲面(图5)。

由图5可知:

(1)随着弹性模量期望值的降低,可靠度指标βf随之下降,其结果是使结构趋于更加不安全;

(2)弹性模量均方差变大,其结果是使βf下降,结构趋于更加不安全;当均方差从0增大到55 G,βf下降得较快,其后下降趋势减慢,

(3)当弹性模量均方差小时,样本离散度小,此时期望值变化对βf影响较大;当弹性模量均方差大时,样本离散度大,此时期望值对βf影响较小。

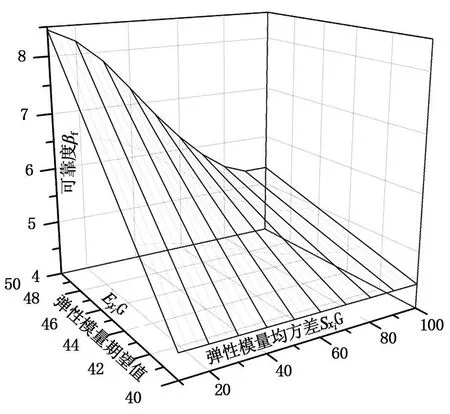
图5 钢管混凝土中拱弹性模量敏感性曲面

4 结论与展望

(1)第一类敏感性问题可用敏感性饼图表示,第二类敏感性问题可用敏感性曲面表示。

(2)第二类敏感性问题能反映可靠度因子均值、均方差对结构可靠度的影响,在实际工程问题中具有实用价值。

(3)实桥算例中,第一类敏感性问题的计算结果与层次分析法的计算结果相吻合,表明ANSYS PDS技术可有效的对结构的第一类敏感性问题进行分析。

(4)实桥算例中,对于结构第二类敏感性问题,ANSYS PDS计算的数据可用于绘制敏感性曲面,直观、定量描述可靠度因子随机变量均值、均方差变化趋势对结构可靠度的影响。

[1]A S NOWAK R I C.Sensitivity analysis for structural errors[J].Journal of Structural Engineering,ASCE,1985:111,1 734-1 746.

[2]M HOHENBIECHIER R R.Sensitivities and importance measures in structural reliability[J].Civil Engineering System,1986(3):,203-209.

[3]A KARAMCHANDANI C A C.Sensitivity analysis for structural errors[J].Structural,1992,11(1):145-153.

[4]佟晓利.钢筋混凝土结构施工期可靠度分析[D].大连:大连理工大学,1997.

[5]赵国藩,贡金鑫,赵尚传.工程结构生命全过程可靠度[M].北京:中国铁道出版社,2004:7-8.

[6]秦权,林道锦,梅刚.结构可靠度随机有限元理论及工程应用[M].北京:清华大学出版社,2006:76-78.

[7]张伟.结构可靠性理论与应用[M].北京:科学出版社,2007:44-48.

[8]KEKE P,PEIYAN H.Fnm method for estimating reliability of existing bridges[J].Journal of Southeast University,2009,25(2):247-251.

[9]GB/T 50283-1999.公路工程结构可靠度设计统一标准[S].中国计划出版社.

[10]彭可可.在役桥梁结构时变可靠性理论及应用[D].广州:华南理工大学,2009.

[11]REH S,BELEY J,MUKHERJES S,et al.Probabilistic finite element analysis using ANSYS[J].Structural Safety,2006,28(1):17-43.

[12]ZHANG Z,TANG W,ZHANG S.Development of special program to calculate structural reliability based on RSM in ANSYS[J].Journal of Ship Mechanics,2007,11(1):102-107.