基于AEMM法的大跨度预制T 梁存梁中的变形分析
2010-08-16周胜怡周志祥
周胜怡,周志祥
(重庆交通大学,重庆400074)
近年来我国高速公路交通量迅猛增长,路面宽度随之增宽,道路交叉亦逐渐增多。在大量跨越被交道路的桥梁建设方案中,少支架施工方案、预制吊装施工方案、顶推施工方案及转体施工方案应用较多。相比较而言,少支架施工需在被交道路上搭设支架,对交通的影响最大;顶推施工和转体施工方案虽然对交通几乎无影响,但措施费较高,建设成本大;预制吊装施工方案不仅对交通影响小,而且建设成本低,因而在4个方案中应用最多。当被交道路较宽时,大跨度预制预应力混凝土T梁的优势就更加明显。
但是,大跨度预制T梁在存梁过程中的变形控制与小跨度T梁相比显得更加复杂。因其在预应力作用下梁体将上拱,加上徐变的作用(对于简支T梁,收缩作用很小),梁体上拱继续增大,导致桥面铺装层厚度不足,影响成桥线形。在考虑徐变对预制T梁存梁过程中变形影响的计算中,徐变计算方法的选取对计算结果的准确性影响很大。本文将运用按龄期调整的有效模量法(AEMM),计算大跨度预制T梁在存梁过程中的由徐变产生的上拱值,最终得出梁体的总变形值[1~3]。
1 按龄期调整的有效模量法(AEMM)
按龄期调整的有效模量法精度较高,更逼近实际的有限元逐步计算法。随着计算机技术的进步和结构有限元方法的应用,复杂结构和复杂过程的徐变问题基本得到完美解决。大跨度预应力混凝土T梁受力过程复杂,预应力损失使作用在梁体上的有效预应力不断变化,截面特性也随着钢束灌浆而改变,需采用逐步计算法来分析不同时间段结构的内力和变形[4~5]。
为了利用数值方法进行逐步计算,按离散的时间点ti(i=0,1,2,……)将整个计算时间划分为若干个时段,对于桥梁结构施工过程的分析,时段的间隔点一般为施工起止、结构体系转换或加卸载的时刻,实际结构中的应力与时间的关系可由图1近似表示,用σi表示ti时刻的瞬时弹性应力,σ*i表示ti-1→ti时段的徐变应力增量。由此可写出时刻tn的徐变引起的应变为:
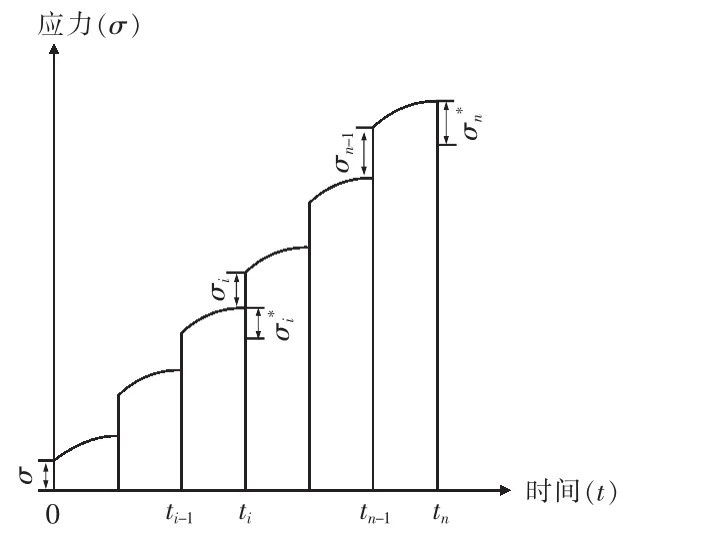
图1 应力与时间的关系Fig.1 The relation between stress and time

同理可写出在时刻tn-1的徐变应变为:

则第n个时段及ti-1→ti的徐变应变为:

利用积分中值定理有:

式中:ti-1≤ tξ≤ ti。

取tξ为i时段的中点时刻,


式中:

式中:E为混凝土相应时段的弹性模量;φ(tn,ti)为混凝土ti时刻加载至tn时刻的徐变系数;χ(tn,tn-1)为混凝土tn-1时刻加载至tn时刻的老化系数。
从式(7)中可以清晰地看出,第n时段内的徐变引起的应力增量和应变增量满足线性关系,因此,可以通过拟弹性方法求解徐变问题,式(6)即为分时段逐步计算法的基本方程,在此算法的基础上,结合具体的单元形式,根据增量平衡理论,得出徐变效应分析的有限单元列阵。
假定在第n个时段内结构所承受的外荷载保持不变,则此时段内的增量平衡方程为:

将式(7)带入式(8)得:

令Δεn=B{Δσn},则方程(8)可以写成:


从式(8)和式(9)可以看出,第n时段内的单元等效结点荷载由应力历史形成的徐变(可以考虑收缩)初应变形成,此时段内的刚度矩阵的形成需考虑时段内折减的换算模量。
2 工程实例
如某高速公路大桥全长502.54 m,双向四车道,半幅桥宽13.5 m,引桥采用跨径50 m的预应力混凝土T梁,预制梁长49.48 m,预制宽度1.60 m,主梁片数8片,主梁肋厚0.20~0.60 m,马蹄宽0.60 m,梁高2.6 m。
主梁采用C50混凝土,钢绞线采用φs15.2,抗拉标准强度fpk=1 860 MPa,公称面积140 mm2。单片梁共布置4束钢绞线,其中N1钢束由9根φs15.2钢绞线编组,N2~N4钢束均由12根φs15.2钢绞线编组。具体见图2。

3 存梁中的变形分析
运用MATLAB7.0开发出平面杆系有限元软件,根据AEMM法编制了徐变分析模块,分别分析不同加载龄期、不同存放时间对50 m预制T梁变形影响规律,以得出预制时的最优控制线性,并给出拟合方程式[6-8]。
3.1 不同加载龄期对预制T梁变形的影响
加载龄期是影响混凝土徐变的重要因素,某些桥梁施工进度要求高,施工周期相对缩短,梁体加载时,混凝土的养护龄期较短,这类情况越来越普遍。因此,研究加载龄期对大跨度预应力混凝土T梁变形的影响规律具有现实意义。本文采用的加载龄期分别为 3,7,14,21,28 d,在不同的龄期施加预应力,统一存放90 d T梁各主要截面的变形值如表1,加载龄期对主梁的影响规律见图3。

表1 不同龄期时各主要截面位移值Tab.1 Displacement of main sections at different loading age

图3 不同龄期对预制T梁变形的影响Fig.3 The effect of prefabricate T beam at different loading age
由表1和图3可见,加载龄期从3 d增加至28 d,构件变形值递减。说明了混凝土加载龄期越短,构件变形越大。其实质上反映了弹性模量对变形影响,即加载龄期越长,弹性模量越大,构件变形越小。但是,当加载龄期大于14 d之后,龄期对变形的影响并不明显,龄期为14,21,28 d的构件变形相差很小。说明了混凝土养护14 d后,其弹性模量已接近规范值,故随着龄期的增大,徐变变形衰减得不再明显。因此在实际工程中,可把14 d作为最优加载龄期,根据实际情况建议加载龄期在10~14 d之间,不要小于10 d。
3.2 不同存放时间对预制T梁变形的影响
在确定了最优加载龄期为14 d后,在14 d的加载龄期下研究不同的存梁时间对预应力混凝土T梁变形的影响规律。对于预制T梁,在张拉预应力钢束以后,往往要简支存放一段时间,才架梁施工桥面系。但在存梁的过程中,混凝土收缩徐变持续发生导致梁体上拱,尤其是徐变,在预应力加载后,相对于收缩,徐变产生梁体上拱值要大很多。梁存放的时间越长,其上拱值越大。若存梁太久,架梁后施工桥面铺装层时将导致其厚度不足,造成后期桥面开裂,桥梁整体性差等问题影响桥梁的耐久性。
图4为最优加载龄期下预制T梁不同存梁时间下的变形。

图4 加载龄期14 d不同存梁时间下梁的变形Fig.4 The disfiguration of beam at different storage time but with the same loading age of 14 d
由图4可见,加载后3~7 d变形较大,7~30 d的变形相对较平缓,综合考虑存梁的变形发展趋势、施工进度要求及预制场地条件等因素,确定30 d为最佳存梁时间。
3.3 最优控制线形的确定
由于大跨度预应力T梁施工过程中产生的上拱值较大,因此施工时需设置向下的预拱度以抵消构件的部分上拱度。预拱度的设置关系重大,若设置过大,成桥后梁体起拱达不到设计值,可能将造成梁体线形下挠,影响桥梁整体美观,对受力不利;若设置过小,架梁后施工桥面铺装层时将导致其厚度不足,造成后期桥面开裂,桥梁整体性差等问题影响桥梁的耐久性。
结构计算时没有考虑二期恒载和活载的影响,经分析把加载龄期14 d和存梁时间30 d计算所得上拱度的60%作为最优预拱度的参考线,见图5。根据此线形拟合出二次多项式:

作为大跨度预制T梁的最优预拱度设置线形。

图5 最优预拱度控制线形Fig.5 Optimal pre-camber alignment
在加载龄期14 d,存放时间30 d的预制T梁施加二期恒载(二期恒载集度按照7.5 kN/m计算),算得变形减去最优预拱度设置线形,见图6。由图中可知,跨中最高上拱值为1 cm左右,完全能够满足桥面铺装层厚度的要求。
4 结论
大跨度预制预应力混凝土T梁,存梁中的变形控制不容忽视,徐变是影响其变形的主要因素。笔者应用有效模量法(AEEM),研究混凝土徐变导致大跨度预制T梁在简支存梁状态下的变形规律,得出以下结论,以指导此类桥梁的施工。

图6 最优成桥控制线形Fig.6 Optimal control alignment at complete stage
1)加载龄期是影响混凝土徐变的重要因素,随着龄期从3~28 d增加,在相同的存放时间下构件变形值非线性递减。当加载龄期大于14 d后,递减缓慢,龄期对变形的影响并不明显,因此最佳加载时间为14 d。
2)存放时间是影响混凝土徐变的又一重要因素,取加载龄期为14 d,随着存放时间从3~3 600 d增加,构件变形值非线性递增。当加载龄期大于30 d后,递增缓慢,考虑到施工进度,确定30 d为最佳存放时间。
3)在综合考虑了龄期和存放时间对构件变形影响后,根据最佳龄期和存放时间提出了预制T梁最优预拱度设置公式。
[1]李国平.预应力混凝土结构设计原理[M].北京:人民交通出版社,2000.
[2]潘立本,刘雁,李建民.预应力混凝土受弯构件的非线性变形[J].土木工程学报,1999,32(4):45 -50.
[3]李之达,邓科李,李耘宇,等.混凝土徐变及其在桥梁预拱度设置中的运用[J].交通科技,2006(6):15 -17.
[4]彭卫,杜时贵.混凝土徐变效应的计算机分析[J].西安公路交通大学学报,1999,2(19):4 -6.
[5]傅作新.工程徐变力学[M].北京:水利电力出版社,1985.
[6]肖汝诚.桥梁结构分析及程序系统[M].北京:人民交通出版社,2002.
[7]刘卫国.MATLAB程序设计教程[M].北京:水利电力出版社,2005.
[8]贺栓海.桥梁结构理论与计算方法[M].北京:人民交通出版社,2003.
