钢－混凝土组合拱桥竖转施工误差分析

吴海军，朱世峰，周志祥

(重庆交通大学土木建筑工程学院，重庆400074)

针对我国西南山岭重丘区山高谷深、U、V形河谷众多的特定地形、地质条件，周志祥教授［1］提出了一种新型钢－混凝土组合拱桥及放张式竖转施工技术(图1，专利申请号:200710048918.8)，其改常规的分节段预制缆索吊装成拱为先竖向施工后自上而下转体成拱，合龙成拱周期由数十天缩短至几小时［1－2］。钢－混凝土组合拱桥结构整体性好、施工便捷、建设周期短、工程造价低、延性抗震能力较强，能够满足跨越山区深谷河流桥梁建设的安全性(特别是施工期间的安全)、经济性及适用性要求，在西部山区40～150 m跨径范围内具有显著的经济、技术效益和推广应用价值。该技术于2007年首次在四川省遂宁市界福路人行桥工程(净跨40 m)得到成功应用，随后在重庆万盛藻渡大桥(净跨75 m)、江津区夹滩笋溪河大桥(净跨100 m)得到了更进一步的发展［3－4］。竖转施工钢－混凝土组合拱桥作为一种全新结构的施工工艺，施工控制尤为重要，作者对施工控制中误差产生的原因及其对结构的受力影响进行了分析，为其完善及在后续工程的推广使用和改进提供了理论依据。

1 转动轴的定位误差分析

竖转钢－混凝土组合拱桥在竖转过程中的水平向偏位主要来自转动轴安装定位时的施工误差，所以转动铰及转动轴的制作及安装精度是关系到顺利转体与成功合龙的关键技术之一，要严格控制转动轴的安装精度，转动轴的定位至关重要。研究发现，转动轴的定位误差主要来自两方面:①同岸两个转动轴同时发生的平移变位;②同岸两个转动轴发生转角变位［3］。

设转动轴在x、y、z方向分别发生的平移位移量为 u、v、w(坐标系规定如图 2);在 x、y、z方向分别发生的转角位移量为θx、θy、θz。下面分别求出当转动轴发生平移变位 u、v、w 以及转角变位 θx、θy、θz时，拱肋跨中合龙处在x、y、z方向分别发生的偏位Δx、Δy、Δz。

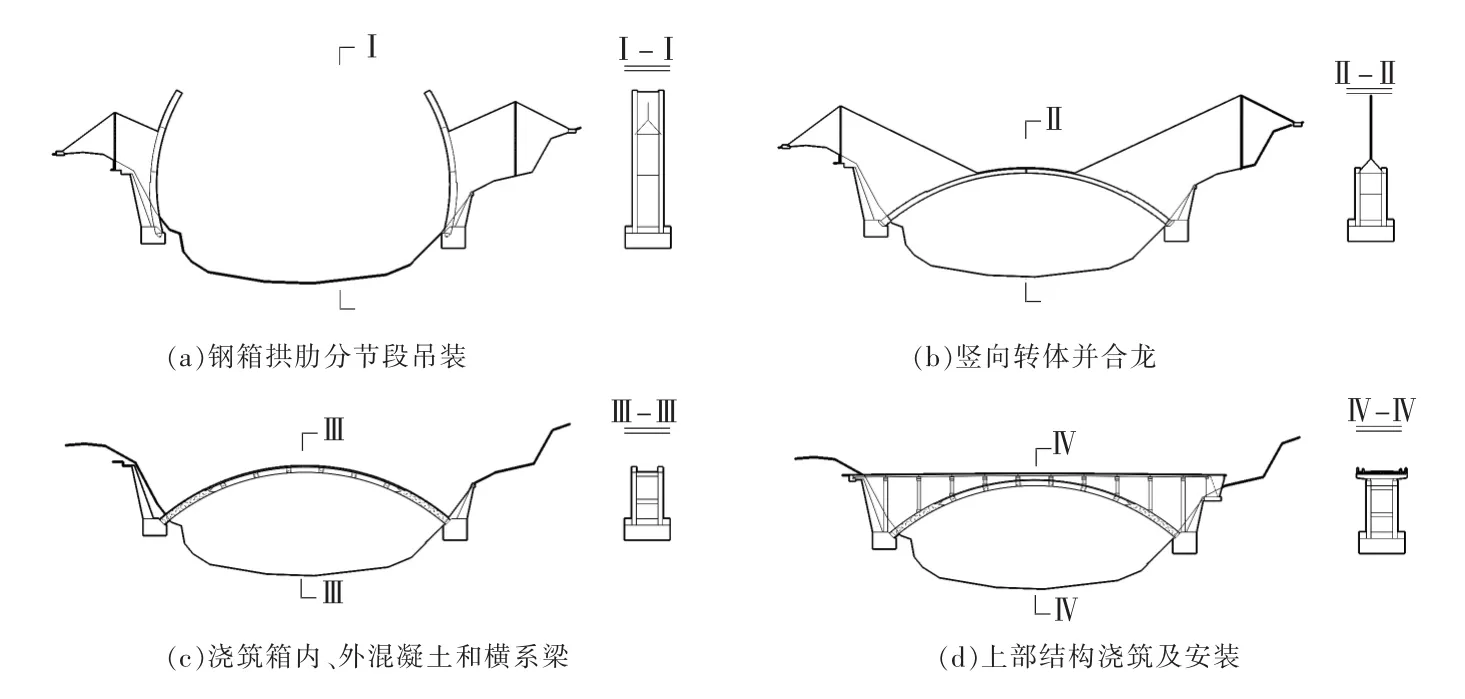
图1 钢－混凝土组合拱桥竖转施工工序示意图Fig.1 Schematic diagram of steel-concrete composite arch bridges erected by rotating down vertically

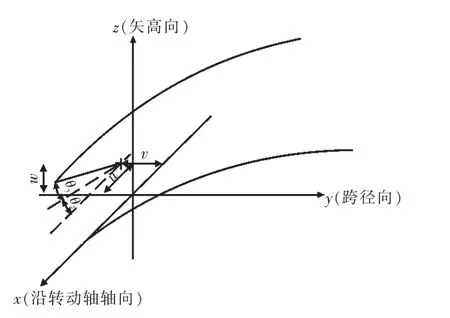
图2 总体坐标系Fig.2 General coordinate system

1.1 平移变位对拱肋跨中合龙精度的影响

同岸的两个拱肋转动轴相对于原设计位置整体发生了平移变位u、v、w，则此时同岸的两个拱肋跨中合龙处也随之整体移动，其在x、y、z方向分别发生的位移量也为 u、v、w(图3)。

图3 转动轴整体平移Fig.3 Integral translation of rotating axis

即在拱肋跨中合龙处的位移量为:

钢箱拱肋结构较轻，竖转扣挂索力相对较小，竖转工艺是将两拱肋采用并联方式同步竖转。竖转前，两拱肋之间设置有足够的横向联系，保证竖转过程中两肋间距不产生太大的扭转或整体偏移。浪风索捆绑在扣点附近，与5 t手拉葫芦锚固在岸上临时浪风地锚，用来调整钢箱拱肋的平面姿态，见图4。在竖转过程中，浪风索基本上处于松弛状态，当进入合龙阶段观测到拱肋发生较为明显的变形和偏位时，可通过收紧浪风索调整钢箱拱肋线形。

图4 拱肋浪风索布置示意图Fig.4 Layout drawing of wind cable fitting on the arch rib

1.2 转角变位对拱肋合龙精度的影响

同岸两个转动轴相对于转动轴中点发生了转角变位 θx、θy、θz。

1.2.1 转动轴发生θx变位

即转动轴是绕着自己转动，所以不会引起两个拱肋的转动轴发生相对错位，因此此时拱肋跨中合龙处的位移量为:

1.2.2 转动轴发生θy变位(图5)

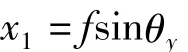
所以:

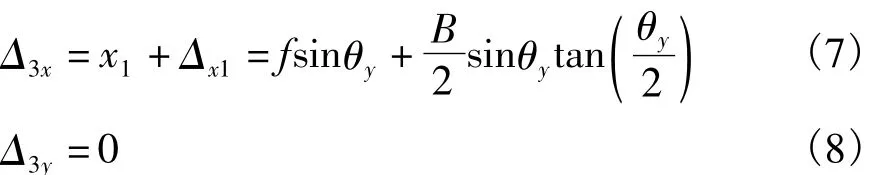
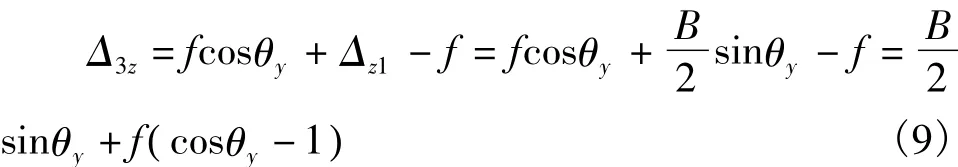
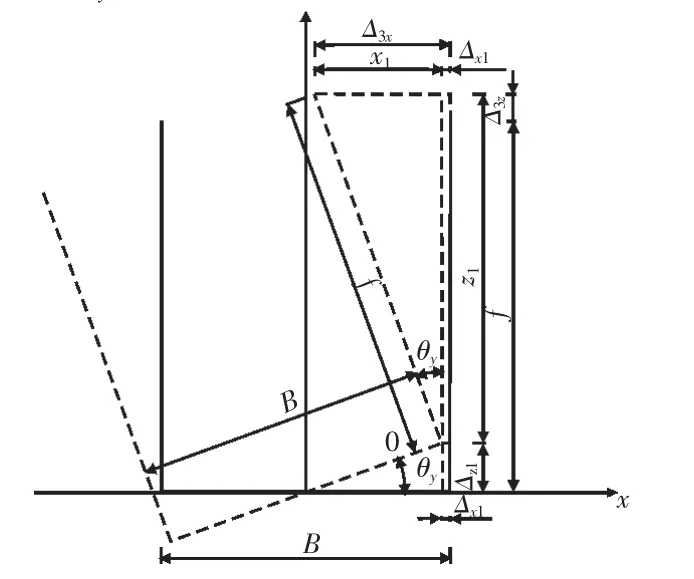
图5 转动轴发生θy变位Fig.5 Rotating axis occurred θydisplacement

1.2.3.转动轴发生θz变位(图6)

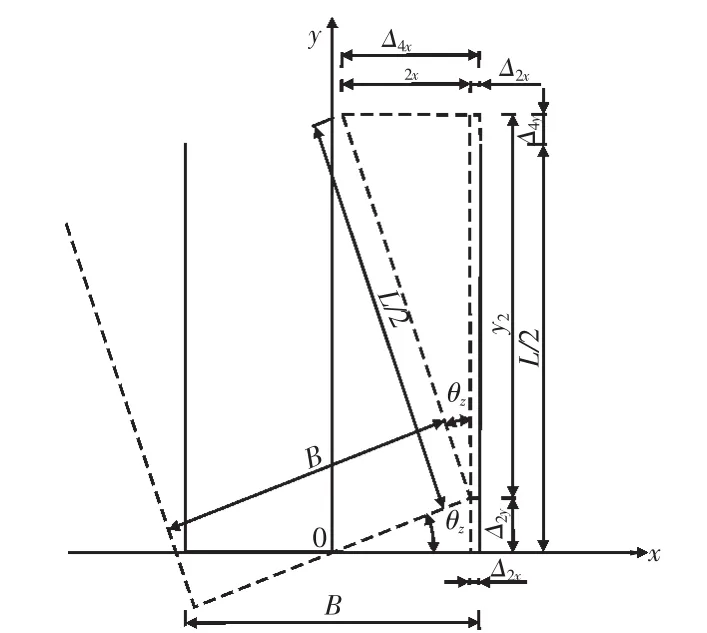
图6 转动轴发生θz变位Fig.6 Rotating axis occurred θzdisplacement

由图6可知:

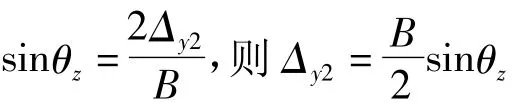
所以:

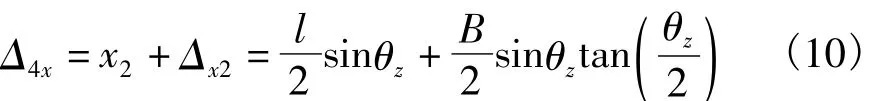
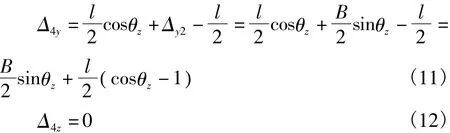
1.3 平移变位及转角变位对拱肋合龙精度总的影响

由式(1)～式(12)可知，同岸两个拱肋转动轴的平移变位及转角变位对拱肋合龙精度总的影响为:

当 θ很小时可取 cosθ≈1，sinθ≈θ。

即，当拱脚转动轴发生平移变位u、v、w以及转角变位 θx、θy、θz时，拱肋跨中合龙处在 x、y、z方向分别发生的偏位为:

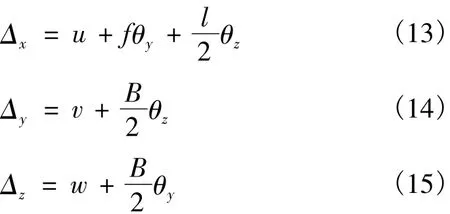
式中:θy=2Δz1/B(Δz1为转动轴沿矢高方向发生的定位误差);θz=2Δy2/B(Δy2为转动轴沿跨径方向发生的定位误差)。

以遂宁市界福路人行桥和万盛藻渡大桥为依托工程［5－6］，对于当同岸两个拱肋转动轴发生不同程度变位时，分别进行计算其对拱肋合龙精度的影响，结果见表1。

表1 转动轴定位误差对合龙精度的影响Tab.1 The effect of rotating axis location error on joining precision

从表1中数据可以看出:①当同岸两个拱肋转动轴发生x、y、z方向定位误差时，对拱肋合龙处x方向(即拱肋的横桥向水平偏位)的精度影响最大，其它两个方向则次之;②定位误差对跨中合龙精度的影响大小与竖转钢－混凝土组合拱桥的两拱肋间距、矢高以及跨径大小有关，但影响程度不同，其中跨径的影响最大;③当同岸两个拱肋转动轴发生定位误差时，对拱肋跨中合龙精度的影响程度随跨径的增大而增大。

2 合龙误差对钢箱拱肋的力学性能影响

由于转动铰和节段钢箱的安装误差对拱肋跨中合龙的横桥向将产生一定的水平偏移，为了跨中的顺利合龙，必须采取相应的措施使其发生反向的水平位移。下面以万盛藻渡大桥为例，通过结构力学和材料力学方法对其合龙后的钢箱拱肋的应力状况进行计算分析。

2.1 横桥向的强迫位移对钢箱拱肋产生的应力分析

2.1.1 计算模型的简化及参数的选取

转动铰的轴与轴孔的间隙仅为1～2 mm，上座耳板与下座耳板之间的间隙仅为2～3 mm，钢箱拱肋在即将合龙时，拱脚部位受较大压力的作用。根据以上几点构造特点和受力特点，转动铰对钢箱拱肋的横桥向的约束相对较强。这里将其简化成固接状态计算，偏于安全。

实际结构的临时横系梁的刚度相对较强，将两条钢箱拱肋连接形成排架结构，可将其简化成单肋进行计算，但应注意简化前后的横桥向抗推刚度相等，简化计算模型如图 7［7］。

图7 简化计算模型Fig.7 Simplified calculation model

为了防止在外荷载P作用下钢箱发生局部屈曲，实际实施过程中的强迫荷载P作用在距离钢箱拱肋跨中位置最近的横隔板处，距离仅为50 cm，相对计算模型中的计算长度L=4 041 cm(转轴中心至跨中的直线距离)很小，忽略其影响，故简化计算模型中将荷载位置移至跨中来进行计算。

2.2 结构力学计算分析

对于一端固接、不考虑自重的悬臂梁，在自由端受外荷载P的作用下，按照结构力学方法，可按式(19)计算其梁端沿力P方向的位移Δ为［5－6］:

针对万盛藻渡大桥的实际参数［4］，下面给出产生不同水平位移所需的外荷载P值。

简化后的截面抗推刚度EI=7.416×109Nm2，L=40.41m。取最不利截面(拱脚截面)作为应力分析对象，依据材料力学公式σ=My/I可计算截面4个角点的正应力［8］，计算结果见表2。

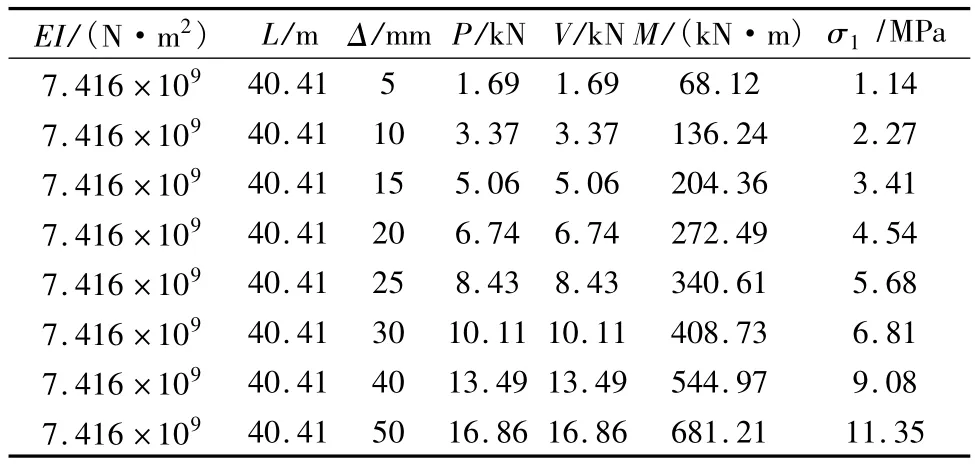
表2 拱脚截面应力计算结果Tab.2 Stress calculating results of springer section

由表2可以得知，剪力V产生的剪应力和弯矩M产生的正应力相比，可以忽略不计。

2.3 不考虑偏差的钢箱拱肋的应力分析

通过有限元程序Midas Civil 6.7.1对全桥进行受力分析，施工阶段分析考虑结构自重和上部恒荷载作用，使用阶段考虑活载和温度的作用。活载采用公路－Ⅰ级，人群荷载3.5 kN/m2，温度采用整体升温25℃和整体降温10℃的温度模式来进行计算。

2.3.1 模型建立

全桥计算跨径L0=76.07 m，钢箱拱肋共划分为200个计算单元。钢－混凝土组合截面采用组合截面模拟，并充分考虑混凝土参与受力的龄期。有限元模型如图8。

图8 结构计算模型Fig.8 Computational model of structure

施工阶段共划分为6个施工阶段:

1)空钢箱合龙，边界条件为铰接;

2)浇筑钢箱内混凝土，不计此阶段的混凝土参与受力，边界条件为铰接;

3)钢箱内混凝土达到龄期参与受力阶段，边界条件为固接，以下均为固接状态;

4)浇筑拱背混凝土，不计此阶段的混凝土参与受力;

5)浇筑混凝土横系梁、拱上立柱和盖梁，全部拱肋参与受力;

6)安装行车道板和桥面铺装等二期恒载。

2.3.2 计算结果分析

不同施工阶段和成桥运营阶段的拱脚截面应力状态计算结果见表3。

表3 不同施工阶段拱脚截面应力计算结果Tab.3 Stress calculating results of springer section about different construction stages

比较表2和表3中的正应力可得如下结论:

1)第一施工阶段，σ1与σ2的绝对值属于同一个数量级。且在Δ =50 mm时 σ1≈2σ2=11.35 MPa，可知此时的钢箱处于低应力状态，仅为Q345q钢材容许应力的6%以内，故不考虑其强度安全。

2)第六施工阶段，在Δ=50 mm时，σ2≈(4～6.5)σ1=44.5～73 MPa，其组合应力最大值σmax=，约为Q345q钢材容许应力的40%，所以可以确保在整个施工阶段不会出现结构强度安全问题。

3)对于运营阶段，强迫合龙产生最不利拱脚截面的正应力(钢)仅为运营阶段拱脚截面正应力(钢)的8%左右，于运营阶段最不利荷载作用下拱脚截面钢箱应力组合MPa，约为钢材容许应力的75%。

综上，强迫合龙对钢箱拱肋的力学性能影响很小。

3 结论

1)分析结果表明，转动轴的平移变位和转角变位是引起定位误差的主要原因。定位误差对合龙精度的影响与拱桥两拱肋的间距、矢高以及跨径大小有关。文中推导了转动轴定位误差对跨中合龙精度影响的计算公式:

可供后续同类工程参考使用。

2)存在跨中横向偏移时的强迫合龙方式对主拱肋力学性能影响不大。以万盛藻渡大桥出现Δ=50 mm为例，其强迫合龙产生的最不利截面(拱脚截面)正应力(钢)仅为运营阶段此截面正应力的8%左右，与运营阶段最不利荷载下此处钢箱应力组合最大值小于钢材容许应力的80%。

3)空钢箱拱肋的刚度小，可调性好，调整后并不产生明显的附加应力，钢箱在转体过程中的应力变化可以由钢箱自身承受，相比常规混凝土拱桥的通过施加临时预应力体系来消除施工过程中产生的拉应力，体现出了其操作简便、安全可靠且经济的优势。

［1］周志祥.一种竖转钢－混凝土组合拱桥［P］.中国专利:CN 200710078521.8，2007－10.

［2］朱世峰，周志祥.钢-混凝土组合拱桥竖转施工体系研究［J］.施工技术，2009，38(07):64 －68.

［3］王勇平.竖转钢-混凝土组合拱桥施工及控制技术研究［D］.重庆:重庆交通大学，2008.

［4］重庆交通大学工程勘察设计院.江津区夹滩笋溪河大桥施工图设计［R］.重庆:重庆交通大学工程勘察设计院，2008.

［5］重庆市路达公路设计咨询事务所.万盛藻渡大桥施工图变更设计文件［R］.重庆:重庆市路达公路设计咨询事务所，2007.

［6］重庆交通大学工程勘察设计院.遂宁市界福路人行桥施工图设计［R］.重庆:重庆交通大学工程勘察设计院，2006.

［7］李廉琨.结构力学［M］.3版.北京:高等教育出版社，1996.

［8］李庆华.材料力学［M］.成都:西南交通大学出版社，1997:108-109.