多进制chirp-rate键控调制及分数傅里叶变换法解调
2010-08-14肇启明张钦宇张乃通
肇启明,张钦宇,张乃通
(1. 哈尔滨工业大学 电子与信息工程学院,黑龙江 哈尔滨 150001;2. 哈尔滨工业大学 深圳研究生院,广东 深圳 518055)
1 引言
在无线通信中为了提高频谱利用率,高阶调制技术被广泛使用。传统的高阶调制技术以正、余弦载波为基础,只有3个参数即幅度、频率和相位可供调制使用,一定程度上制约了调制的性能。例如,以相位作为键控对象的 MPSK调制虽然具有恒包络特性,但由于其调制星座点均匀分布于一个圆周之上,随着调制进制数的增加,星座图变密,抗干扰能力降低;以幅度作为键控对象的MQAM调制
虽然具有较好的抗干扰能力,但不具有恒包络特性,功率效率较低;以频率作为键控对象的MFSK调制具有恒包络特性并且抗干扰性能理想,但是带宽效率较低。Chirp信号是另一类基本信号,较正、余弦信号多了一个称之为调频率(chirp-rate) 的参数,用chirp信号作 (副) 载波能够获得一个额外的可供调制使用的自由度,从而可以设计新型调制方式。二进制chirp-rate调制 (也称chirp-BOK) 是基于 chirp信号参数键控的一种最简单的调制方式,最早于20世纪60年代作为一种扩频通信方式被提出,此后的研究表明其具有较强的抵抗多径干扰和快速移动造成的快衰落影响等优良特性[1,2]。采用二进制 chirp-rate调制的简单通信方案具有低成本和低功耗的优势,比较适合于室内近距离高速传输等解决方案,chirp扩频(啁啾展频)方案已经成为IEEE 802.15.4a建议的物理层标准之一。然而,传统的chirp信号分析和处理方式主要基于chirp信号理想的自相关特性采用匹配滤波的方式,随着使用的chirp信号参数的增加,匹配滤波处理变得复杂,一定程度上制约了多参数 chirp信号在一般无线通信系统中的广泛应用。近年来,随着分数阶傅里叶变换的理论的逐步完善以及与快速傅里叶变换(FFT)复杂度近似的离散分数傅里叶变换算法的逐渐成熟,分数阶傅里叶变换已经成为 chirp信号分析和处理的有力工具[3~7]。经分数阶傅里叶变换,chirp信号在某最优阶次的分数傅里叶域上具有理想的能量聚集特性(冲激特性),并且该最优变换阶次以及该变换域上能量聚集的位置与 chirp信号的chirp-rate及中心频率2参数间具有确定的对应关系[8]。根据上述特性,本文首先提出了一种利用chirp信号不同的chirp-rate承载代表不同信息符号的新方法,称为多进制 chirp-rate键控 (MCrSK,multiple chirp-rate shift keying),并采用分数傅里叶变换法进行解调。仿真表明,在 AWGN信道中,保证一定的接收信噪比条件下,该方法允许采用更高进制的调制并具有优于MPSK的误码率性能。进而,鉴于chirp信号中心频率参数独立于chirp-rate参数,将MCrSK和中心频率参数键控联合使用,其实质是MCrSK与MFSK的级联,能够在一定的误码率条件下进一步提高调制进制数。MCrSK的带宽效率优于MFSK,而误码率性能劣于MFSK,通过灵活地搭配MCrSK与MFSK在级联使用中的权重,可以获得带宽效率与误码率性能的灵活折中。
本文中,第2节对分数阶傅里叶变换以及chirp信号的分数阶变换特性进行介绍;第 3节给出MCrSK调制、解调原理及其误码率性能仿真及分析;第4节分对MCrSK与MFSK的联合使用进行了研究;第5节是结束语。
2 Chirp信号的分数阶傅里叶变换性质
分数阶傅里叶变换(FrFT, fractional Fourier transform)是傅里叶变换的一种广义形式,将信号在时—频平面上由时间轴逆时针旋转任意角度的新的变换域上进行描述,能够揭示信号的频率时变规律。根据经典定义方法,函数 f(t)的分数阶傅里叶变换可表示为
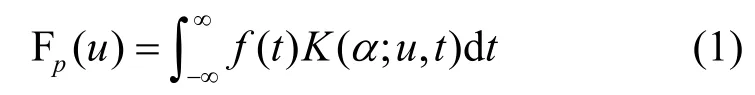
其中,p为分数傅里叶变换阶次;α为分数阶傅里叶域 (u轴) 从时间轴逆时针旋转的角度,α= πp/2;非整数阶分数傅里叶变换的积分核函数K(α; u, t)定义为

当p=1时,分数傅里叶变换退化为傅里叶变换;当p=0时,变换将保持原函数不变。
复形式chirp信号的时域表达式为

其中,φ为初始相位;f0为中心频率;k为调频率即chirp-rate。当k>0时,chirp信号的瞬时频率随时间增大,常称为up-chirp,反之则称为down-chirp;T时间内,瞬时频率变化范围为kT,称为扫频带宽。将式(3)写为

则 exp(jπkt2)为一个中心频率为 0的 chirp信号;exp[j(2πf0t+φ)]为一个频率为f0的单音调制信号。根据式(1)、式(2),T时宽(-T/2≤t≤T/2)chirp信号的p(非整数)阶分数傅里叶变换为
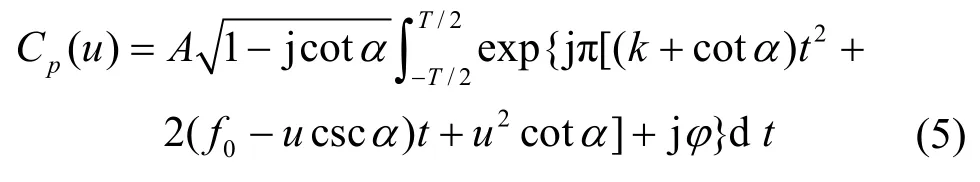
对于 p∈[- 1, 1],当且仅当 cotα=-k即p=2arccot(-k)/π 时

如果仅考虑 Cp(u)的分数傅里叶域的幅度谱特性,则

其中,Sa(·)表示辛格函数。|Cp(u)|对称中心位于u0|p=f0sinα处,第一过零点间宽度为|2sinα/T |。以上分析可知,chirp信号的chirp-rate决定了p∈[-1, 1]唯一的最优变换阶次po,中心频率f0唯一决定了在po阶分数傅里叶域上最优的能量聚集位置,后者也可以看作是频率为f0的单音调制引起的分数傅里叶域上谱线搬移。对 chirp信号进行非最优阶分数傅里叶变换时,分数傅里叶域谱不具有聚集性质,而且随着变换阶次p偏离p的程度Δp增大,|Cp(u)|的峰值明显下降。综合考虑具有不同 chirp-rate的chirp信号,具有大chirp-rate的chirp信号的|Cp(u)|随Δp增加下降得更快,如图1所示,chirp信号的chirp-rate分别为3.077 7、1.962 6、1.376 4、1、0.726 5、0.509 5、0.158 4 (相应的 po分别为-0.2、-0.3、-0.4、-0.5、-0.6、-0.7、-0.8) 并具有相同的时宽。因此,通过分数傅里叶变换性质可以对 chirp信号的chirp-rate和中心频率2参数进行识别。
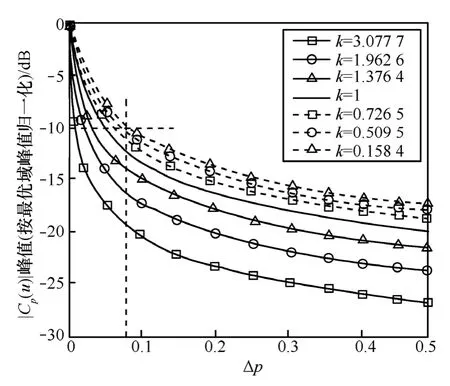
图1 具有不同chirp-rate的chirp信号的|Cp(u)|随Δp的变化情况
3 MCrSK调制及分数傅里叶变化法解调
基于 chirp信号的分数傅里叶域特性与其chirp- rate、中心频率2个参数的明确关系,可以设计一个在发送端利用对 chirp信号的 chirp-rate和中心频率参数进行键控以承载信息,并在接收端利用分数傅里叶变换对接收的 chirp信号进行参数识别以实现解调的新型多进制调制、解调方案。本节暂只考虑采用chirp-rate单参数的多进制键控的调制、解调原理及其性能,联合使用chirp-rate和中心频率2个参数的方案及其性能于下一节中进一步讨论。
3.1 MCrSK调制及解调原理
根据式(4)、式(6)和式(7),f0=0的chirp信号即零中频chirp信号exp(jπkt2)的chirp-rate k不同,则相应的最优分数傅里叶变换阶次po不同,因此设定一个chirp信号chirp-rate的集合{ki},在发送端利用多进制信息符号对{ki}的元素进行键控,则输出的(基带)chirp信号的chirp-rate承载信息并可以保持包络(输出功率)恒定。在接收端,假设已取得符号同步,对接收信号(中频或零中频)分别做一系列与{ki}中各chirp-rate相对应的分数傅里叶变换,设中频为fIF,则相应的各最优阶分数傅里叶域幅度谱峰值将位于u0|p=f0sinα。因此将各预定阶次分数傅里叶域上的u0|p位置(或邻近区域)作为检测点进行峰值比较,并将具有最大峰值的分数傅里叶变换阶次pe所对应的ke(ke∈{ki})作为判决结果,即可实现解调,并按符号输出。由式 (7) 可知,不同阶次分数傅里叶域幅度谱|Cp(u)|具有一个与 p有关的系数|(1-jcotα)1/2|,并且辛格谱的零点—零点宽度|2sinα/T|也与p有关,导致不同chirp-rate的chirp信号在其对应的最优阶次分数傅里叶域上的能量聚集能力存在差异,因此进行检测点峰值比较以前需要进行归一化处理,具体做法是将各检测点幅度按其输入匹配的 chirp信号时的幅度峰值进行归一化,从而保证了对不同符号检测能力的一致性。MCrSK调制及基于分数傅里叶变化法解调的原理图如图2所示。调制结构采用与MFSK、MPSK等调制类似的多进制键控一般结构,接收端将所接收的 chirp信号先进行符号同步,然后进行一系列预定阶次的分数傅里叶变换,并进行比较判决,整个过程可在数字信号处理器中完成,分数傅里叶变换由离散算法实现,计算量与FFT运算保持相同的数量级[6, 7]。
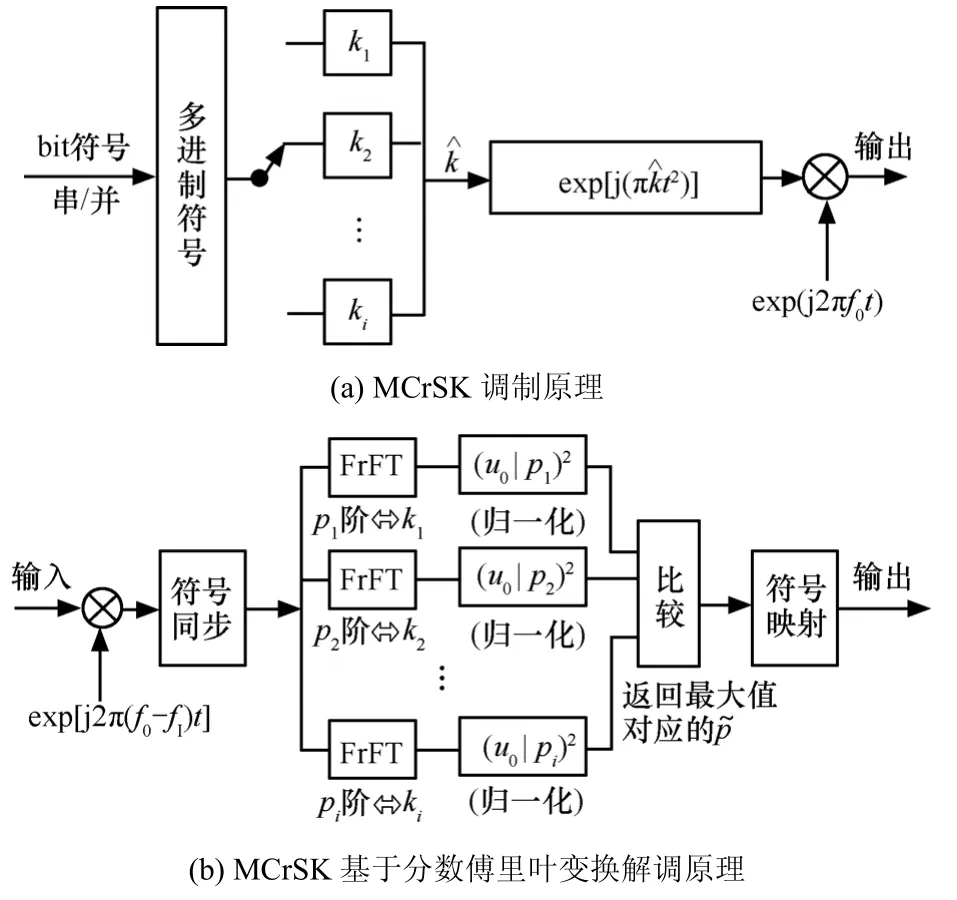
图2 MCrSK调制及解调原理
3.2 Chirp-rate集{ki}的设计
Chirp-rate集{ki}中相邻的ki与ki+1对应的2个最优分数傅里叶变换阶次pi与pi+1的间隔Δp决定了采用分数傅里叶变换进行解调时对相邻符号的区分度,即Δp决定了相邻符号间的干扰程度。根据Δp与ki、ki+1的关系
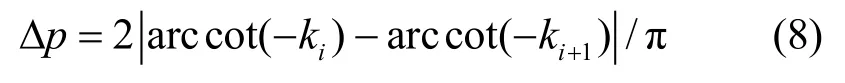
为了降低相邻符号间的干扰,{ki}的设计应使得Δp尽可能大。然而,由于 chirp信号的时宽-带宽积BT=kT2,对于固定的符号持续时间 Ts,具有大的chirp-rate k的chirp信号将占用大的带宽,{ki}的最大取值受到可用带宽的限制。因此{ki}的设计需对上述2个方面进行折中。{ki}的设计有2个特例,其一是{ki}仅包含一个k,此时k不能承载信息,当kT>>2/T,即chirp扫频宽度远大于bit符号的带宽时,是一种chirp扩频调制;其二是{ki}仅包含调频率相反的一对k与-k,此时退化为所谓的chirp-rate调制 (chirp-BOK 调制),文献[9]给出 chirp-rate调制采用基于分数傅里叶变换的非相干解调的性能分析。
3.3 MCrSK误码率仿真及分析
首先给定用于解调的分数傅里叶变换最优阶次p的变化范围,仿真中令p∈[0.2,1.8],根据符号进制 M,将 p变换范围等分为Δp。设第一个符号对应的最优分数傅里叶变换阶次为p1=0.2,则第i个符号对应的pi=0.2+(i-1)Δp,则根据{pi}可得{ki}。在AWGN信道中,在不同的Eb/N0下分别对8、16、32进制chirp-rate键控抗干扰性能进行仿真,为便于比较,以误比特率(BER) 给出,并与 8PSK、16PSK、32PSK以及16QAM和32QAM的BER理论曲线进行比较,如图3所示。当能够保证接收的chirp信号具有足够的信噪比时,较高进制的MCrSK具有优于MPSK的抗干扰性能而略差于 MQAM。这是由于当进制数较高时,MPSK星座图将非常稠密,抗干扰性能恶化严重,而MCrSK用于承载信息的 chirp-rate是一种频率随时间变化的规律,较之固定的相位参数,抗干扰能力更强;MQAM是一种正交调制方式,而MCrSK相邻符号间不具有正交性,因此 MQAM 抗干扰性能优于MCrSK,然而MQAM不具有恒包络性,功率效率低于MCrSK。
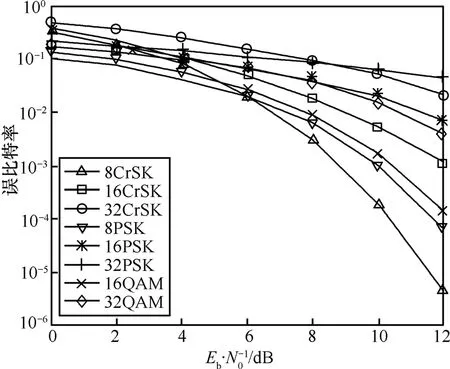
图3 MCrSK与MPSK、MQAM的误比特率性能比较
4 MCrSK与MFSK级联
式(4)进一步可表示为

其中,exp(j2πfct+φ)是频率为 fc的单音载波,exp(jπkt2)为中心频率为 0 的 chirp 信号,exp(jπfjt)为频率为fj的单音副载波。由于参数k与fj相互独立,因此可以将对k的键控和对fj的键控联合使用,即MCrSK与MFSK级联使用。MCrSK的chirp-rate集{ki}的设计已于前一节中给出,下面考虑MFSK频率集{fj}的设计。为了保证具有相同chirp-rate的、中心频率fj不同的chirp信号在分数傅里叶域上可以区分,根据时宽为T的中心频率为 fj的chirp信号在最优阶分数傅里叶域上的谱峰值位于 u=f0sinα,且第一零点间距离为|2sinα/T|,{fj}的设计应使得相邻频点间隔 Δf能够使得 Δ u 满足 Δ u=|Δ fsinα|>|2sinα/T |,即Δ f>2/T,与MFSK的频率集设定规则是一致的。当确定了{ki}和{fj}分别具有 n1和 n2个元素,n1CrSK-n2FSK调制可以由一个n1×n2的调制矩阵M表示为

当n1、n2均为2的整数幂时,串行比特码元每N=lbn1+lbn2个码元构成一个2N进制符号,将N个码元分成N1=lbn1和N2=lbn22组,分别构成n1和n2进制的2个子控制符号,可以唯一确定M矩阵中的一个元素(kx, fy),即键控输出一个调频率为kx,中心频率为fy的chirp信号。如图4所示为n1=8、n2=8时64进制调制星座图的示例,k和f两方向上没有约束关系。
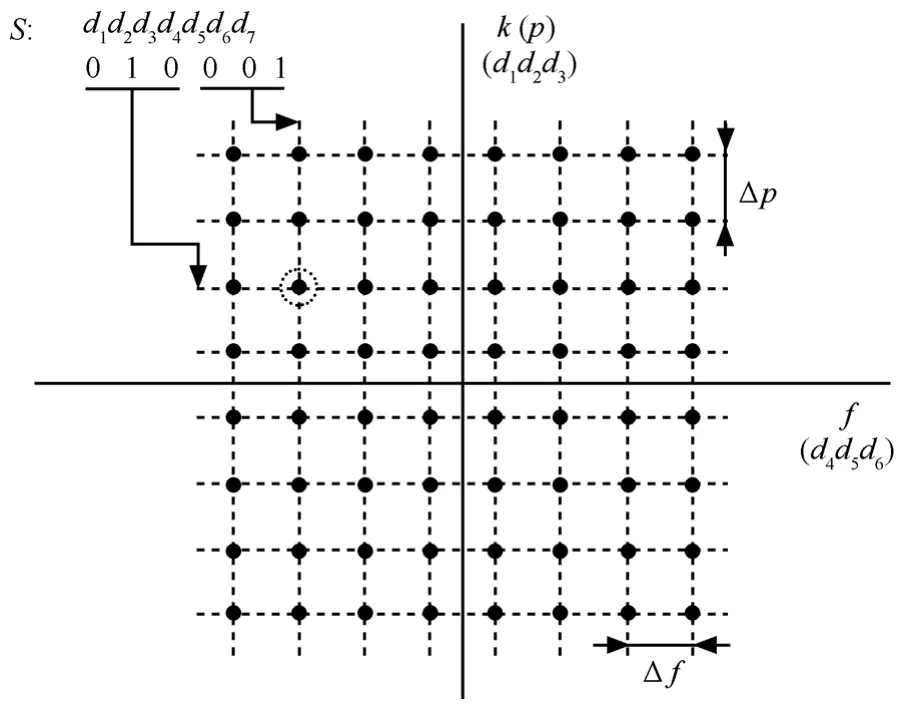
图4 64进制MCrSK-FSK星座图的一个示例(8CrSK-8FSK)
MCrSK与MFSK级联调制器可由如图2(a)所示结构与一个普通的MFSK调制器级联获得,解调器较图2(b)所示结构多一个环节:首先对接收信号做n1次阶次分别对应{ki}的分数傅里叶变换,并且将各分数傅里叶域上由{fj}决定的 n2个可能出现的幅度峰值的位置uj|αi(j=1, 2, …, n2) 设为检测点,这样共有 n1×n2个检测点 (或检测区域) ,将这些检测点归一化峰值进行比较,具有最大值的检测点对应分数傅里叶变换阶次以及在该阶分数傅里叶域上的位置可以唯一确定输出的调制符号,从而实现解调。AWGN信道中,MCrSK-MFSK的误比特率仿真曲线如图5所示,其中3条实线分别为64进制级联调制的3种组合方式,即16CrSK-4FSK、8CrSK- 8FSK和4CrSK-16FSK,可见这3种方式的误比特率性能逐渐改善,这是由于MFSK的误比特率性能优于MCrSK,MCrSK与MFSK的不同配比可以调整联合调制的抗干扰性能。此外,仿真结果还表明,64进制级联调制性能显著优于64PSK和64QAM方式,而且同样保持恒包络特性。

图5 MCRSK-FSK与MPSK、MQAM的误比特率性能比较
设比特宽度为 Tb,仅采用调频率键控时,M进制符号宽度为Ts=TblbM,由于chirp-rate k是变化的,不同符号键控输出的chirp信号的扫频带宽Tsk也是变化的,其最大宽度由最大的chirp-rate kmax决定。则调频率键控方式的带宽效率 ηMCRSK满足

MFSK 的信道带宽理论值为 Rb(M+3)/2lbM(相干MFSK),则MFSK的带宽效率ηMFSK
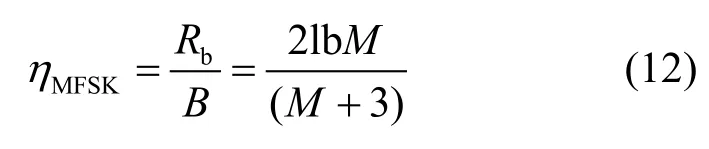
因此,当 kmaxTs2<(M+3)/2即用于 MCrSK 的chirp信号的最大时宽-带宽积 TBmax<(M+3)/2时,MCrSK具有优于MFSK的带宽效率。因此MCrSK与MFSK级联使用可以通过2种调制方式的灵活搭配,获得抗干扰性能与带宽效率间的折中。鉴于未来无线传输多样化的业务模式对抗干扰性能和带宽效率要求的差异,MCrSK与MFSK级联使用具有很大的潜在应用价值。
5 结束语
本文对多进制 chirp-rate键控及其基于分数傅里叶变换的解调方法进行了研究。仿真表明,在AWGN信道中,对于一定的误比特率性能,多进制chirp-rate键控较MPSK允许更高的调制进制,并具有恒包络特性。多进制 chirp-rate键控可以与MFSK联合使用,并同样采用基于分数傅里叶变换的解调方法,联合调制能过获得较单独使用多进制chirp-rate键控更优的误比特率性能,但需要占用更大带宽。联合调制通过调整多进制chirp-rate键控与MFSK的比重,能够获得对频谱效率与误比特率性能的灵活折中。文中关于所提出方式的性能的讨论是基于接收机符号已经取得同步这一假设前提,具体的符号同步方法有待进一步研究。此外,所提出的调制解调方案在非AWGN信道如多径信道、双弥散信道中的性能等将在后续研究中给出。
[1] WINKELY M R. Chirp signals for communications[A]. Proceedings of IEEE WESCON Conference [C]. Piscataway, NJ, USA,1962.14-17.
[2] TSAI Y R, CHANG J F. The feasibility of combating multipath interference by chirp spread spectrum techniques over Rayleigh and Rician fading channels[A]. Proceedings of IEEE 3rd International Symposium on Spread Spectrum Techniques and Applications[C]. New York ,NY, USA, 1994. 282-286.
[3] ALMEIDA L B. The fractional Fourier transform and time- frequency representations[J]. IEEE Trans on Signal Processing,1994, 42(11):3084-3091.
[4] TAO R, DENG B, WANG Y. Research progress of the fractional Fourier transform in signal processing[J]. Science in China Series F: Information Sciences, 2006, 49(1): 1-25.
[5] CANDAN C, KUTAY M A, OZAKTAS H M. The discrete fractional Fourier transform[J]. IEEE Trans on Signal Processing, 2000, 48(5):1329-1337.
[6] YEH M H, PEI S C. A method for the discrete fractional Fourier transform computation[J]. IEEE Trans on Signal Processing, 2003, 51(3):889-891.
[7] TAO R, ZHANG F, WANG Y. Research progress on discretization of fractional Fourier transform[J]. Science in China Series F: Information Sciences, 2008, 51(7): 859-880.
[8] ZHAO X H, TAO R, ZHOU S Y. A novel sequential estimation algorithm for chirp signal parameters[A]. Proceedings of the 2003 International Conference on Neural Networks and Signal Processing[C].Nanjing, China, 2003.628-631.
[9] 邓兵, 陶然, 平殿发. 基于分数阶Fourier 变换的chirp-rate 调制解调方法研究[J]. 电子学报, 2008, 36 (6): 1078-1083.DENG B, TAO R, PING D F. Study on chirp-rate modulation and demodulation based on fractional Fourier transform[J]. Acta Electronica Sinica, 2008, 36 (6): 1078-1083.
