大跨度连续刚构桥的弹塑性动力时程分析

2010-08-13刘大明刘文浩

山西建筑 2010年26期

刘大明刘文浩

1 概述

在各国抗震设计规范中,抗震设计的基本原则是“小震不坏,中震可修,大震不倒”。由于交通中断造成直接、间接经济损失巨大。且对于许多大型桥梁空间结构来说,采用线性结构分析并不是真实的安全设计[1]。因此,除要进行结构在“小震”作用下的弹性分析外,还要进行“大震”作用下的弹塑性动力反应分析。

本文利用刚度退化三线性模型对某大跨度连续刚构桥实体工程进行了弹塑性动力时程分析,确定了桥墩塑性铰对结构抗震性能的影响。算例分析结果可为同类桥梁工程的抗震设计提供参考。

2 刚度退化三线性模型弹塑性动力分析

2.1 刚度退化三线性模型

该模型的主要特点是:用三段折线代表正、反向加载恢复力骨架曲线,并考虑钢筋混凝土结构或构件的刚度退化性质(如图1所示)。

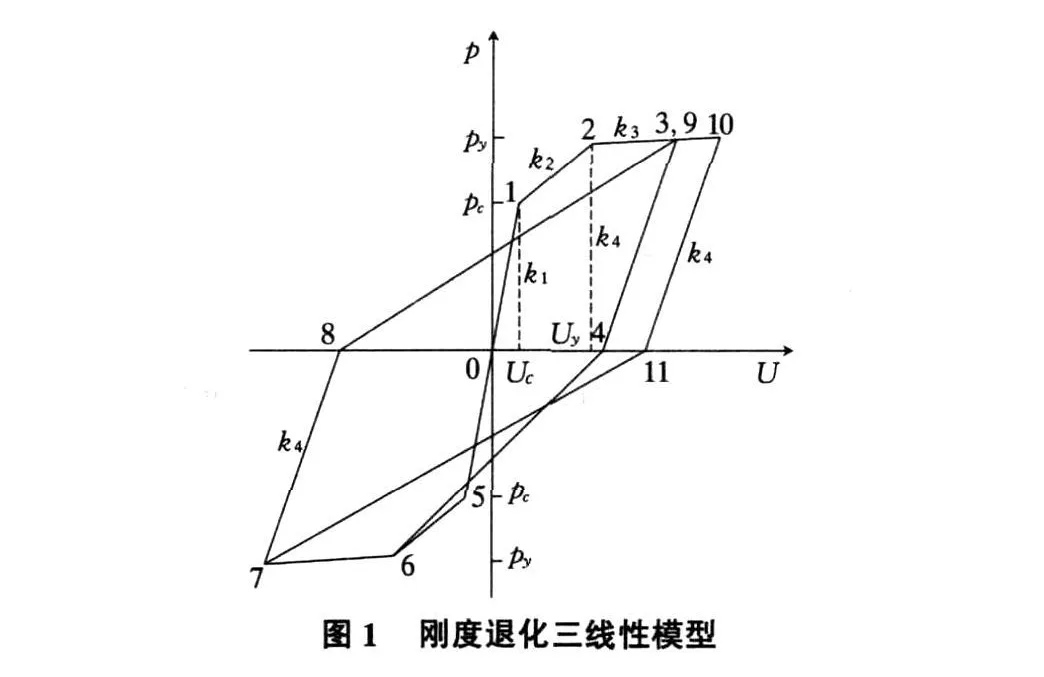
1)三折线的第一段表示线弹性阶段,此阶段刚度为k1,点1为开裂点。第二段折线表示开裂至屈服的阶段,此阶段刚度为k2,点2为屈服点。屈服后则由第三段折线代表,其刚度为k3。2)若在开裂至屈服阶段卸载,则卸载刚度取k1。若屈服后卸载,则卸载刚度取割线2的刚度 k4。3)中途卸载,卸载刚度取 k4。4)1-2段(2-3段)卸载至零,第一次反向加载时直线指向反向开裂点(屈服点)。后续反向加载时直线指向所经历过的最大位移点。

2.2 刚度退化三线性模型中的特征参数

若已知构件开裂荷载 pc及弹性刚度k1,开裂点(点1)即可确定。屈服点(点2)则可根据构件屈服荷载 py及屈服点割线刚度k4确定。k4表示为:

其中,αy为屈服点割线刚度降低系数。

显然,若已知 pc,py,k1,αy,即可完全确定模型(如图1所示)。对钢筋混凝土梁、柱,pc,py通常取为梁、柱开裂弯矩与屈服弯矩;k1则为梁、柱截面弹性弯曲刚度或梁、柱弹性弯曲刚度[2]。

3 工程实例

3.1 工程概况

大桥设计荷载为公路—Ⅰ级,主桥为75 m+136 m+75 m三跨预应力混凝土变截面连续刚构箱梁桥,全长286 m。全幅桥箱梁采用分离式单箱双室截面,C50混凝土,顶板宽度为20.25 m,底板宽13.25 m,翼缘宽3.5 m,最大悬臂长69 m,墩顶梁段高为7.5 m,跨中梁段高为 3 m,箱梁顶板厚 0.26 m,边跨端部现浇段腹板厚度65 cm,其余梁段腹板采用65 cm,55 cm,40 cm三种厚度,中间设过渡梁段,箱梁采用三向预应力体系。

主墩墩身采用单箱双室的箱形薄壁断面,墩宽13.25 m,墩厚3 m,壁厚 0.6 m。主墩承台采用整体式承台,承台厚度4 m,横桥向两端做成弧形,承台封底混凝土厚度0.5 m。每个主墩基础采用12根D250 cm的钻孔灌注桩,桩基按嵌岩桩设计。桥面铺装采用10 cm厚沥青混凝土。

3.2 桥墩和桩计算模型中特征参数

根据文献[3]～[5]和上述理论及公式,文中模型做了简化计算,只以墩柱在初始状态下的受力来计算模型特征参数,不考虑在地震过程中结构受力状态改变对模型特征参数的影响,计算结果见表1。

表1 特征参数 kN◦m

3.3 弹塑性动力时程分析结果

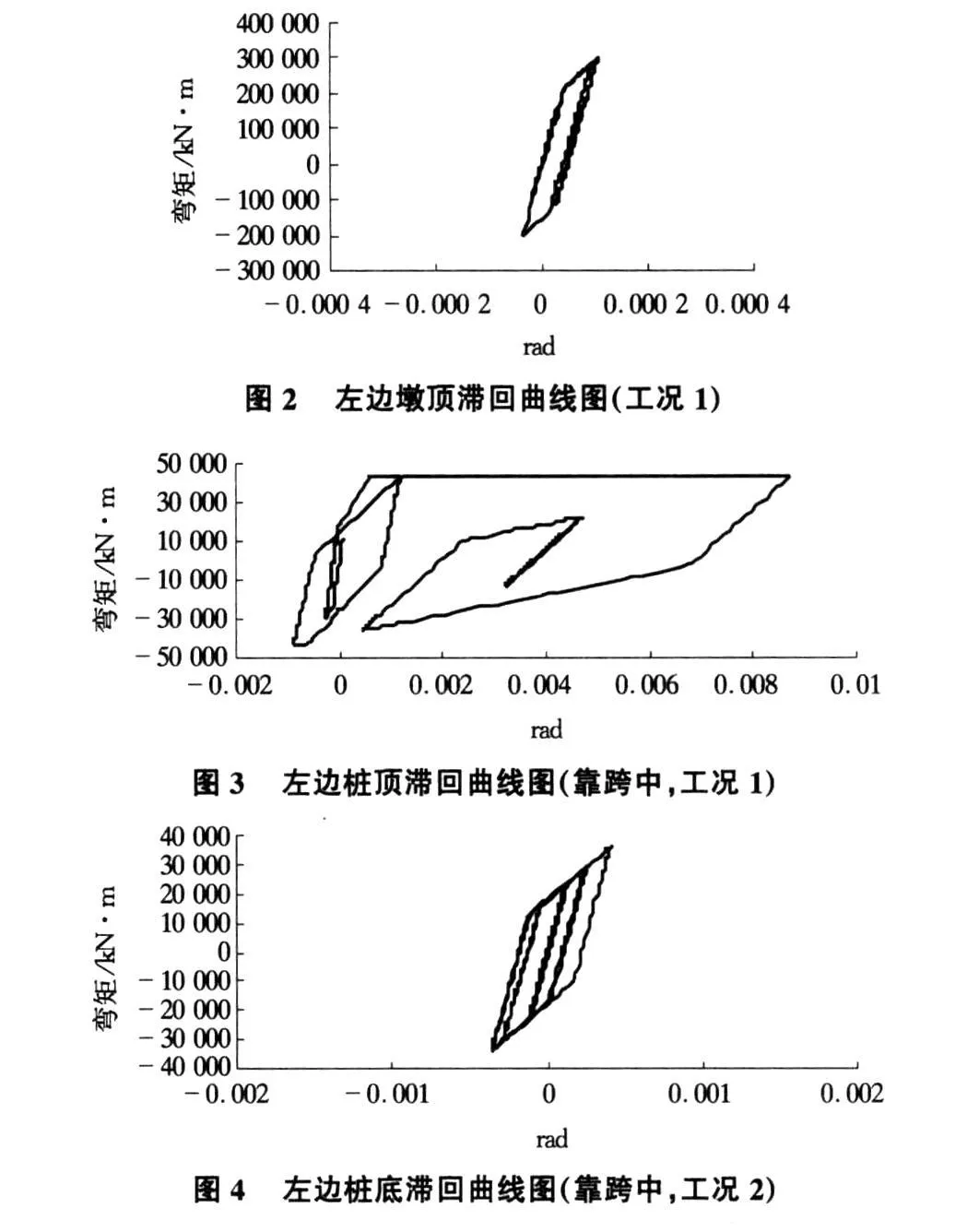
计算模型选取了工况1(自重+纵向地震+0.5竖向)和工况2(自重+横向地震+0.5竖向)两种工况,同时为了能够体现桥梁局部位置的塑性性能,在计算时将地震波峰值加速度调整为0.62g(9度罕遇地震)。计算结果见图 2～图4。

从图2～图 4可以看出:

1)工况1作用下,墩顶截面滞回曲线为一棱形,但其中并无水平段。表明截面已进入开裂阶段但仍未进入屈服阶段,图中棱形所围成的大小表示截面开裂后所消耗的地震能量。桩顶和桩底的滞回曲线都出现了水平段,表明截面进入屈服阶段,塑性铰变形已十分明显,表明铰已进入完全塑性状态,其中桩顶的塑性铰变形大于桩底变形。由此可以看出,此桥梁结构的薄弱环节主要是在桩顶,桩底和墩顶截面。

2)工况2作用下,桩顶滞回曲线出现了水平段,表明截面进入屈服阶段,但塑性铰变形比工况1要小,塑性铰也已进入完全塑性状态。桩底截面的滞回曲线为一棱形,但其中并无水平段,表明截面已进入开裂阶段但仍未进入屈服阶段。由此可以看出,此桥梁结构的薄弱环节主要是在桩顶、桩底。鉴于此,作者认为有必要提高桩的自身刚度,同时在桩顶和桩底位置局部加大配筋并且加密箍筋,提高其延性。