基于格林函数声表面波换能器的分析

张永刚

（安徽理工大学 电气与信息工程学院，安徽 淮南 232001）

0 引言

声表面波是指沿着弹性固体表面传播的弹性声波[1]，在弹性固体单个表面上镀一层叉指形状的金属薄膜电极，就构成声表面波换能器，它是声表面波器件的核心。在换能器电极上加载激励信号电压，弹性固体内就会有声表面波的产生。适当改变金属电极的间隔、数目、长度以及形状等参数，就能够得到声波的不同传输特性。声表面波器件的功能就是通过电极对介质内传播的声表面波进行处理来实现信号采集与处理的功能[1]。近年来，声表面波器件在通信领域的地位越来越重要，随着半导体工艺水平的提高，声表面波器件的应用领域不断扩大：从信号采集、卫星通信、雷达制导、无线遥控、广播电视到移动通信、无绳电话等都广泛使用声表面波器件。

格林函数法是分析声波器件的一种常用方法，这种方法就是是针对特定边界条件建立相应的格林函数，用它表示系统中某点的激发源在另一点建立的响应，任意场量都可写成格林函数同物理激发量的空间分布的卷积[2]。格林函数直接表征了对应物理系统的基本特征，分析格林函数就可获得系统的基本物理特征。

1 格林函数分析原理

在换能器电极上加载激励电压，换能器的介质内就会产生声表面波，换能器产生声表面波的传递函数和电极上的电荷分布之间存在线性关系，所以可以由电极上的电荷分布计算出声波的大小，可以把电极上的电荷分布看成产生声表面波的源。格林函数表示如下[1]：

其中 Ge( x)为静电场部分， Gs( x,ω)为声表面波部分，Gb( x,ω)为体声波部分。

在声表面波器件中，由于换能器表面的机电耦合不是很强，其它作用比声表面波作用弱得多，对表面换能起主要作用的是静电荷。若其它作用省略，只考虑 Ge( x)，这种近似分析称为准静态分析，那么有：

相应的格林函数 Ge( x) 表达式为[1]：

其中0ε是真空中的介电常数，常数上式中格林函数 Ge( x)表达式中的积分值为无穷大，考虑假设在x=x0有一个+δ电荷，在 x=-x0处有一个对应的-δ电荷，这时有：

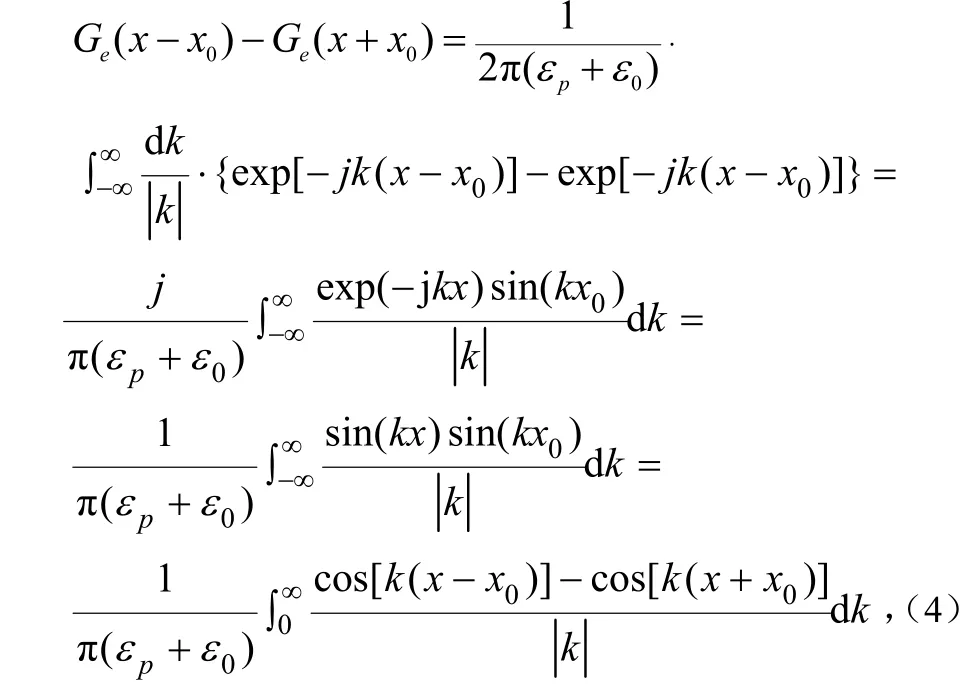
根据定积分公式：

可以得到：

式（6）和式（3）都是 Ge( x)的表达式，它们之间相差一个常数，这个常数的值为无穷大。只要电荷总和为 0，式中正电荷的常数总能和负电荷的常数相抵消。所以在总的电荷为0的条件下，用式（6）代替式（3）是允许的[1]。

当已知电极上的激励电压，求换能器上的静态电荷分布时，通常可以不采用上述完全解析的方法，可以采用解析方法和数值方法相结合方法[3-4]：把换能器上每个电极等分成偶数段（如图 1所示），每一段的中心位置依次设为：x1,x2,…,xn，(n=1,2,…,m, m为小段总数)，设电极上每一小段的长度为Δx。

如果设换能器电极上的激励电压为ψ(x)，电极上电荷分布为σ(x)，激励电压和电荷分布之间的关系为：

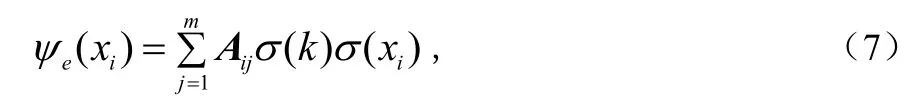
这个方程的系数是由元素Aij组成的矩阵 A。当Δx→0时,m→∞，此矩阵方程和下面公式相同：

其中系数矩阵元素：

对于系数矩阵Aij:当Δx→0,且i=j时,Aij趋于无穷大。这个式子也无法计算出正确的结果,消除无穷大的方法是令:可知系数矩阵A是对称矩阵，即 Aij= Aji。

可以把式（7）进行变换，以电极上的激励电压为已知量，电荷分布为未知量，方程可转化为：

方程系数是由Bij组成的矩阵B，根据矩阵A的性质可知矩阵B是矩阵A的逆矩阵而且有：

2 计算结果

设声表面波换能器的压电基体上有5个电极，电极宽度等于电极之间的间隙宽度。本文计算的第一种情况是在换能器中间电极上加载单位直流电压，其他4个电极接地（如图2所示），采用格林函数方法得到的静态电荷分布如图3所示。为了对结果加以对比，我们采用有限元方法计算出相同电压激励下的静态电荷分布[5]，把两种方法计算结果放在一起进行比较（如图 3所示）。可以看出格林函数法结果和有限元法的的结果是基本一致的，图3中纵坐标数值要乘以10-10。

图2 中间电极加单位直流电压激励

中心电极加载单位直流电压，其他电极接地的激励方式是计算换能器电荷分布的基本方式，对于其它电极上的不同电压激励，除了可以采用前面描述的式（11）来直接求解外，也可以通过把上述求解的结果叠加来求电极上的电荷分布。

第二种情况是在换能器相邻的电极上加载极性相反的单位直流电压（如图 4所示）。采用采用格林函数法计算，得到换能器电极上的电荷分布如下页图5所示。

图4 正负相反加载单位直流电压激励

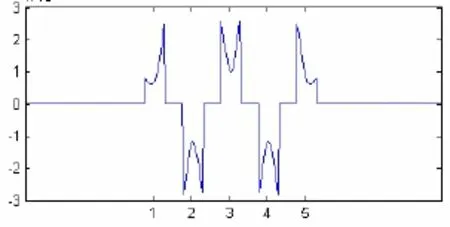
图5 正负相反加载单位直流电压时的电荷分布

图5（纵坐标数值要乘以10-11）中，边缘电极和中间电极上的电荷分布差别较大，原因是换能器中不同位置电极的周围环境不同，造成每个电极上电荷分布也会有所不同。比如中间的电极的左右环境是相同的，所以这个电极上的电荷分布是左右对称的，而换能器边缘的电极左右电极排列不同，即它的左右环境不同，同时也不同于中间电极，所以边缘电极上电荷分布是不对称的，也不同于中间电极的电荷分布。

3 结语

在换能器电极上加载激励电压，换能器介质将电信号转换成声信号，这是物理学中的一类非常普遍的问题，格林函数是解决这一类问题的适用方法，本文采用格林函数法对声表面波换能器的表面换能问题进行分析，计算换能器电极上的静态电荷分布并与有限元法的计算结果进行比较，两种方法的结果是一致的。格林函数法对声表面波换能器的分析可以用来求声换能器的其它参数,为声表面波器件的设计优化与建模提供精确的数据。

[1] 水永安.声表面波与声表面波器件讲义[M].南京:南京大学,1998:202-205.

[2] Arfken G, Mathematical Methods for Physicists[M]. 3rded. New York: Academic.1985:78-94.

[3] Morgan D P. Surface-Wave Devices for Signal Processing[M]. New York:Elsevier. 1985:49-52.

[4] Milsom R F, Reily N H C, Redwood M. Analysis of Generation and Detection of Surface and Bulk Acoustic Waves by Interdigital Transducers[J].IEEE Transactions on Sonics and Ultrasonic.1997,24(03):257-263.

[5] 张永刚.基于有限元法的声表面波换能器电荷分布的静电解[J].声学与电子工程,2007(03):31-33.