基于灰色关联的远程火箭炮装备保障能力评估研究*

2010-08-11陈红军赵德才

舰船电子工程 2010年2期

陈红军殷硕赵德才

(解放军炮兵学院五系合肥 230031)

1 应用的基本理论

1.1 灰色系统理论的基本概念

灰色系统理论[1]是一种研究少数据、贫信息不确定性问题的新方法。灰色系统理论以“部分信息已知,部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象,主要通过对“部分”已知信息的生成、开发,提取有价值的信息,实现对系统运行行为、演化规律的正确描述和有效监控。社会、经济、农业、工业、生态、生物等许多系统,是按照研究对象所属的领域和范围命名的,而灰色系统却是按颜色命名的。我们用“黑”表示信息未知,用“白”表示信息完全明确,用“灰”表示部分信息明确、部分信息不明确。相应地,信息完全明确的系统称为白色系统,信息未知的系统称为黑色系统,部分信息明确、部分信息不明确的系统称为灰色系统。

1.2 灰序白化

白化是将不确定性,不可量化的数据量转化为确定性的可量化的数据量的一种数据处理手段。先运用模糊理论,再通过白化方法可首先对缺乏定性信息的指标进行定性分析,而且不会引起定量指标与定性指标之间的不一致,再分析定量指标,从而得到指标的权重。

1.3 灰色关联

灰色系统关联分[2]析法实质上是一种多因素统计分析方法,以各因素的样本数据为依据,用灰色关联度来描述因素间关系的强弱、大小和次序,主要是分析各个组成因素与整体的关联大小,其操作的对象是各因素的时间序列,而对于多指标综合评估对象可以把比较序列看成由被评事务的各项指标值构成的序列,参考序列是一个理想的比较标准,受到距离评估方法的启示,选最优指标数据和最劣指标作为参考数列,比较各方案与最优和最劣方案的关联程度,来评估各个方案相互之间的优劣。由灰色关联分析的基本思想可知,由于关联性是曲线间几何形状的差别,关联度可以用关联系数来表示,因此我们以曲线间的插值大小作为一种衡量关联度的标准。

设母因素时间数列和子因素时间数列分别为:

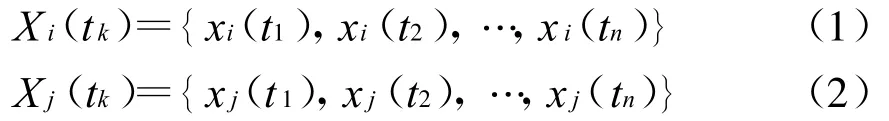
式中xi()为母因素,xj()为子因素,tk为时间。

记tk时刻xj对xi的关联系数为ξij(tk),其绝对差值为

记各时刻的最小绝对差为

各时刻的最大绝对差为

则母因素与子因素两曲线在各时刻的相对差值,即时刻对的关联系数,可用下式来表示

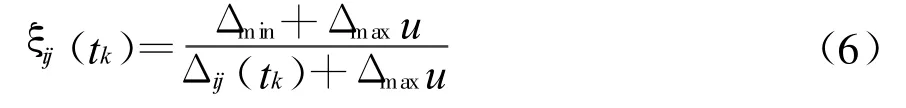
其中u称为分辨系数,u∈[0,1]。

2 目标评估体系的建立及指标的计算

2.1 目标评估体系的建立

远程火箭炮系统装备保障能力评估的目的是评估一个部(分)队在使用远程火箭炮系统的装备保障人员及机构对所属装备的保障能力,是否能够协调和提高装备保障力量的整体效能,最大限度的发挥装备保障力量的装备保障潜能。

图1 远程火箭炮系统装备保障能力评估体系示意图

评估工作的目的性主要由评估指标体现。由于装备保障系统涉及多种属性,所以,为了反映评估的目的,需要明确评估目标(体系)。任何评估指标(体系)都是为其目标(体系)服务的。根据评估目的,远程火箭炮系统装备保障能力评估的体系根据保障要素划分如图1所示。

远程火箭炮系统装备保障能力评估体系要素主要包括保障方案、保障设备、保障供给、技术资料、保障设施、保障人员数量与技术等级、保障机构、装备管理、资源利用率9个方面。其中保障规划、技术资料、保障设施、保障机构、装备管理、属于定性指标;保障设备、保障人员数量与技术等级、保障供给、资源利用率为定量指标,用实际数据进行信息处理,用灰色白化的方法综合处理定性和定量指标。

2.2 定量指标的计算

定量指标可由公式或部队实际计算,由于篇幅所限,不一一列出,这里仅列出装备供给需求量的计算公式[3]:

其中,C为装备物资总需求量;C1为装备物资消耗需求量;C2为装备物资损失量;C3为装备物资机动量;C4为战后保持战备的需求量。

2.2.1 C1的预计

按照武器装备、弹药、维修器材等三大类物资的预计方法。对于武器装备战时报废损失需补充数量的预计。分三种情况,一是受击报废的需要补充;二是严重损坏中来不及修补并需要投入使用的需要补充;三是自然磨损报废需要补充。

对于第一种情况报废装备的数量可用下列公式计算:

其中,S指某种武器装备预计受击报废数;W为某种武器装备的现有数量;N为某种武器装备的损坏率;n为某种武器装备报废数占总损坏数的比例。

对于第二种情况,严重损坏的装备若不能或不必要展开大修,则应予以补充,其补充的数量也可用上述公式计算,其计算公式中的n表示某种武器装备严重损坏数占总损坏数的比例,其他字母的含义与上相同。

对于第三种情况自然磨损报废装备的数量预计,一般按照参战装备的10%左右预计。弹药消耗和维修器材的计算也参见有关公式。

2.2.2 物资损失(C2)的预计

在战斗过程中,装备物资损失量可按照消耗量的20%～30%左右预计。

2.2.3 装备物资机动量(C3)的预计

为了在意外和某些特殊情况发生时,能够保证装备物资的供应,对装备物资需求量预计时,应有一定的机动量。总的装备物质机动量一般应保持在总需求量的15%～25%左右。

2.2.4 战后保持战备需求量(C4)的预计

战备需求量在装备物资总量预计中占有较大的比重,战后要保持多大的战备储备标准由总部确定,战备储量的计算方法参考前面C1的方法进行预计。

3 模型建立

3.1 模型各量的声明

设在对装备保障评估中,有n项指标,m项决策,第i项决策的各项指标为:

式中i=1,2,…,m。xi(1),xi(2),…,xi(n)为各项指标的数值。

将各项指标值无量纲化处理:

式中x0(j)为第j项指标的标准值。各项指标的权重 λ={λ1,λ2,…,λn},对于权重的确定我们可以用灰序白化和模糊理论的方法。

3.2 指标的确定

3.2.1 对指标的灰序白化

定量指标经过无量纲化处理后即可。这里着重介绍对定性指标的处理方法。定性指标的灰序白化的关键是构造决策集的优越性二元对比矩阵,通过优越性定性标度矩阵,得到决策集定性排序。并对决策集进行相对优度的量化,从而实现定性指标的白化。具体步骤如下:

我们对决策集中第i项决策与第j项决策的第k项定性指标的优越性进行比较,规定表示优越性的定性排序标度在0,0.5,1之间取值。若第i项决策比第j项决策优越,取 keij=1,keji=0;若第j项决策比第i项决策优越,取keij=0,keji=1;若同样优越,取keij=keji=0.5,则可得到优越性二元对比矩阵为

根据上面得到的二元对比矩阵,得到决策集优越性的定性排序。根据日常语气习惯,我们选择8个语气助词来划分等级,并利用线性插值插入量值,如表1所示。

表1 等级划分表

如此可以得到不同决策所有定性指标的相对标度,这样所有指标的无量纲化就全部完成。

3.2.2 确定指标权重

假设由灰序白化的方法确定指标的权重序关系为λn＞λn-1＞…＞λ1,即按照各指标对保障性工程的影响大小由n到1递减排列。自此我们只确定了指标的大小顺序,并没有得到具体的量值,即权重还不知道。考虑到装备保障任务的不同,实际使用时会对各项指标有不同的要求,利用模糊理论将人的主观经验判断进行分级分类,即可得到指标的权重。具体的处理过程同定性指标的处理方法。

3.3 对各决策进行关联分析

关联系数是灰色关联分析中用于表示待评价数列中该指标值与最优参考数列中相应指标值接近程度的数值,值越大表示接近程度越高,即越接近最优。

将指标无量纲化处理后,对各项决策的各项指标我们取最优值,原则是:越大越优型指标我们选最大值,越小越优型指标我们选最小值。这样我们确定了指标的最有参考数列(1)(2),…,(n)。令R=|(j)-Xi(j)|,第 i项决策的第j项指标的关联系数ξij由下式得出[4]:

式中,u为分辨系数,u∈[0,1],人为给定,u越小分辨力越大,通常取u=0.5。

将m项决策的指标数列对最优参考数列的加权关联度,从大到小排列,即可得到在n项指标下的决策优劣顺序。

4 实例数据分析

现对某部队远程火箭炮系统装备保障能力评估各指标权重数据列表如表2所示,各指标的权重由本模型提出的灰色白化的方法得出,在这里不详细求解。

表2 指标权重列表

假设对已装备火箭炮的5个作战部(分)队进行装备保障能力评估,通过评估组的打分,建立装备保障方案综合评价表如表3所示。

表3 装备保障方案综合评价表

对指标灰色白化[6],其中的定量指标保障设备,保障人员数量与技术等级,保障供给,资源利用率已经过无量纲化处理。

下面对定性指标进行白化处理:

分析部队的装备保障能力,对于评价指标“保障方案”而言,专家认为部(分)队1要比部(分)队2,3,4,5都要优越。其中,1与2比较介于十分和非常之间,1与3比较介于稍稍和较为之间,1与4比较介于显著和十分之间,1与5比较介于同样和稍稍之间。根据表1,就有5个部(分)队的同一指标={1,0.131,0.646,0.229,0.774}。利用同样的方法,我们可以得到不同部(分)队的其他定性指标的值,将它们写入表3。

对决策进行关联分析:

将表3中的指标代入到指标关联系数公式,得到关联系数:

ξ1={1,0.7877,1,0.5632,0.4965,1,1,0.6498,0.4107}

ξ2={0.3444,1,0.6954,0.6498,0.6498,0.3719,1,0.8838,0.3719}

ξ3={0.5632,0.4107,0.8087,1,0.3444,0.3565,0.3333,0.6954,0.4965}

ξ4={0.3719,0.3887,0.6689,0.3719,0.3887,1,0.4107,0.6554,1}

ξ5={0.6689,1,0.6554,0.6954,0.4107,1,0.4965,0.6689,0.3333}

再由各决策关联系数及指标的权重,得到决策的加权关联度

γ1=0.0971

γ2=0.0730

γ3=0.0584

γ4=0.0628

γ5=0.0791

由此,比较决策的关联度,可得到决策1较优。我们进一步分析可知,部(分)队2在保障方案、保障人员数量与技术等级和资源利用率方面需要改善,部(分)队3在保障设施、保障人员数量与技术等级和保障机构方面需要改善,部(分)队4保障方案和技术资料方面需要改善,部(分)队5在资源利用率方面需要改善,而此结果与实际情况相符,从而说明该模型的有效性。