数字图像的逆滤波复原
2010-08-10陈华玲寥家亮
陈华玲,冯 桂,寥家亮
(华侨大学 信息科学与工程学院,福建 泉州 362021)
1 引言
在各类图像系统中,由于图像的传送和转换,如成像、复制、扫描、传输、显示等,总要造成图像的降质[1],典型表现为图像模糊、失真、有噪声等,这一过程称为图像的退化。相反的,将图像退化的过程模型化,并据此采取相反的过程以求得原始(清晰)图像即为图像复原技术。图像复原的质量和可靠性通常依赖于对图像退化信息了解的确切程度。所以模糊图像复原一般分为两个步骤:一是通过系统辨识方法求解退化函数(PSF),二是采取相应算法由退化图像和退化函数复原出原始图像。
系统辨识方法通常有测试靶方法、互相关方法和图像辨识系统方法[2]。前两种方法适用于手头有一套摄像系统,对系统输入的一些特殊信号得到输出,然后根据输入和输出计算系统传递函数,即PSF。后一种方法则试图根据退化图像本身来确定退化的PSF。笔者从离焦模糊和运动模糊产生的原因出发,结合模糊图像与频谱图的对应关系,应用Hough变换估计出退化参数,然后利用逆滤波方法对模糊图像进行复原。
2 逆滤波复原原理
原始图像 f(x,y)经过一个算子或者系统 h(x,y)作用后,与噪声 n(x,y)叠加而形成观察到的退化图像 g(x,y)[3]。其数学表达式为
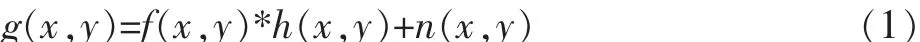
式中:h(x,y)是一个综合了所有退化因素的函数。式(1)对应的频域表达式为
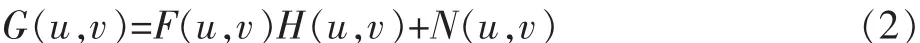
由式(2)可以得到
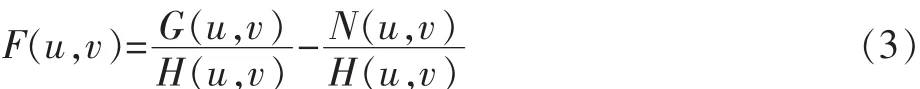
将 F(u,v)进行傅立叶逆变换得到的 f′(x,y)即为原始图像的最佳估计。这个过程就是逆滤波的基本原理。在不考虑噪声的情况下,g(x,y)=f(x,y)*h(x,y),则有

由式(4)可见,如果 H(u,v)在 uv 平面上取零或者很小,就会带来计算上的困难,使复原结果与预期结果有很大差距。一般情况下,逆滤波器并不正好是1/H(u,v),而是 u 和 v的某个函数,可记为 M(u,v)。 M(u,v)常称为复原转移函数或处理传递函数。通常取M(u,v)为
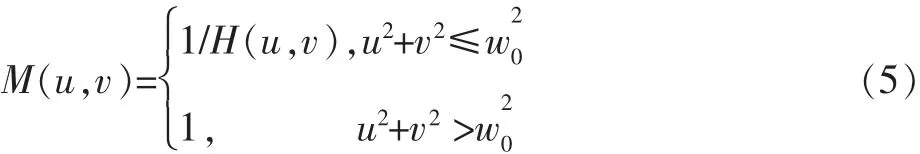
式中:w0的选取原则是将H(u,v)为零的点除去。这种方法使得复原结果的振铃效应较明显。改进的方法是取M(u,v)为
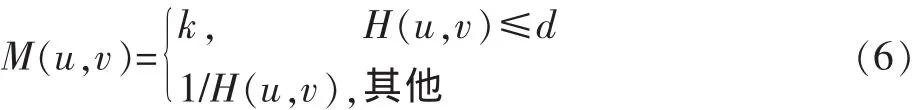
式中:k和d均为小于1的常数,而且d选得较小为好。
3 模糊原理及参数估计
3.1 离焦模糊图像模型
在几何光学条件下,对于线性移不变成像系统,离焦模糊图像的退化模型可以抽象为一圆盘函数[4]

式中:r为退化模型唯一的模糊参数,是待求参数。对应的离散傅立叶变换可表示为[5]
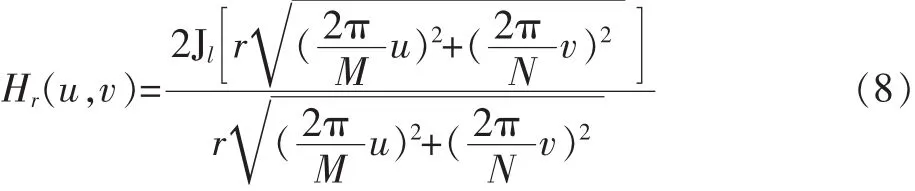
式中:Jl[]表示一阶第一类贝塞尔(Bessel)函数,M和N为二维傅立叶变换尺寸。由一阶第一类贝塞尔函数的性质可知,Hr(u,v)在频率域的第一个暗环(零点)的轨迹为

根据式(9),可以由离焦模糊图像的二维傅立叶变换频谱图G(u,v)的第一个暗环(零点)所对应的空间频率u和v 求出模糊半径 r,从而求出点扩散函数 hr(x,y)和 Hr(u,v)。
3.2 运动模糊图像模型
对匀速运动模糊图像来说,设物体沿水平方向移动了d个像素,则退化模型可以描述为[6]

式(10)对应的离散傅立叶变换可表示为[7]
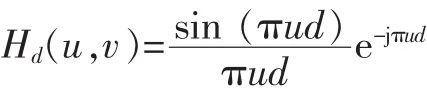
Hd(u,v)的频谱幅值为。 由此可知,的零点位置分布在1/d的倍数处。零点所在频谱图像上体现为暗条纹,而曲线包络的峰值点在频谱图像上体现为亮条纹。因此,只要求出条纹间距D,根据式(11)计算相移量 d,点扩散函数 Hd(x,y)和Hd(u,v)也就确定。

3.3 参数估计
对退化图像做二维傅立叶变换得到退化图像频谱图,再通过霍夫变换求取暗环半径及条纹间距。求取暗环半径过程如下:
1)对频谱图进行边缘检测得到边缘图像。
2)根据先验知识,分别确定第一暗环半径范围,从而减小搜索半径。
3)圆的参数方程可写为:a=x-rcos θ,b=y-rsin θ。 将边缘点代入式中求出参数(a,b)之值。由于圆心位于图像中间区域的某个范围,因此如果(a,b)位于这一范围,则将相应的累加阵 H(a,b,r)中的元素加 1,否则加 0。
4)找出 H(a,b,r)中元素的最大值,即是对应半径为r,圆心为(a,b)的暗环。
求取条纹间距过程与暗环半径相似,不同的是直线参数方程表示为ρ=xcos θ+ysin θ。对检测到的直线求取出直线间距,再利用公式(9)和(11)算出模糊半径与相移量。
4 实验结果
选用256×256的Lena图像作为原始图像,利用Hough变换在频率域上估计退化参数,采用改进的逆滤波器对模糊图像进行复原。表1与表2分别是利用Hough变换求取的暗环半径和条纹间隔同实际大小的比较,可见,结果与真实值比较接近。图1是模糊半径为5及相移量为15的逆滤波复原结果。
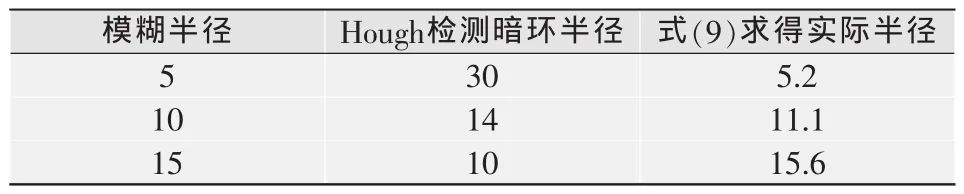
表1 利用Hough变换求取的暗环半径同实际大小的比较
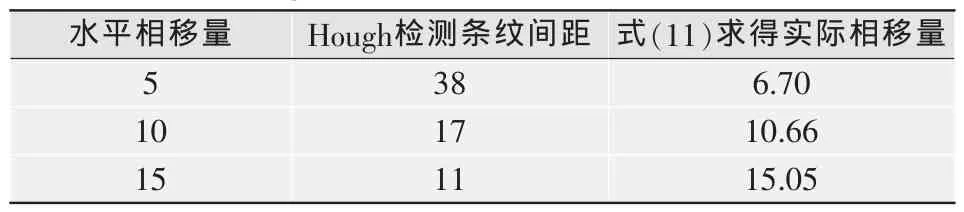
表2 利用Hough变换求取条纹间隔同实际大小的比较
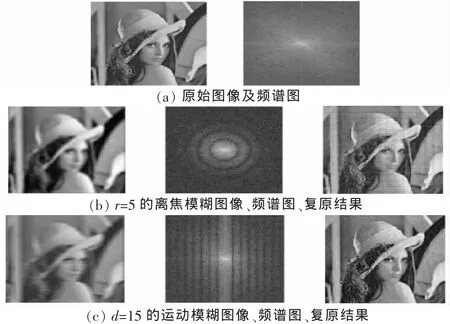
图1 Lena图像实验结果
图像的复原效果比较好,不过在图像中仍然存在一些振铃波纹,可采用巴特沃斯低通滤波器等对图像进行处理,从而减小振铃波纹现象。实验结果表明,改进的逆滤波器简单易实现,复原结果较好。但Hough变换估计退化参数的准确性有待进一步提高。
5 小结
数字图像复原是图像处理中的一项重要技术。笔者采用改进的逆滤波器,避免了一般逆滤波器的普遍病态性,算法简单易实现,且计算运行时间少。实验结果证明了该方法的可行性和有效性,适用于模糊图像的快速复原。
[1]张雪峰,张全法,冯小星.一种扫描图像几何畸变的数字校正方法[J].电视技术,2003(9):78-79.
[2]OMG.The Common Object Request Broker:Architecture and Specification:Version 3.0[S].2002.
[3]CONZALEZ R C.数字图像处理[M].北京:电子工业出版社,2003.
[4]PAVLOVIC G,TEKALP A M.Maximum likelihood parametric blur identification based on a continuous spatial domain model[J].IEEE Trans.Image Proc.,1992,1(10):496-504.
[5]LAY K T,KATASGGELOS A K.Image identification and restoration based on the expectation-maximization algorithm [J].IEEE Trans.ASSP,1990,38(7):1180-1191.
[6]LOKHANDE R.Identification of parameters and restoration of motion blurred images[M].[S.l.]: ACM Press,2006:301-305.
[7]王文发,刘彦保.傅立叶变换用于图像处理时的特性分析[J].延安大学学报,2006,25(3):22-24.
