模糊物元模型在地下水水质评价中的应用

张俊华，杨耀红，陈南祥

（1.华北水利水电学院资源环境学院，郑州 450011；2.华北水利水电学院水利学院，郑州 450011）

模糊物元模型在地下水水质评价中的应用

张俊华1，杨耀红2，陈南祥1

（1.华北水利水电学院资源环境学院，郑州 450011；2.华北水利水电学院水利学院，郑州 450011）

在模糊物元分析的基础之上，与熵权法相结合，构建了用于评价地下水水质的模糊物元分析模型。在进行水质评价时，把水质的分类等级作为物元的事物，以它们的各项评价指标及其相应的模糊量值构造复合模糊物元，通过计算与理想模糊物元之间的海明贴近度，实现对水样水质的等级评价。采用熵权法确定权重，避免了人为因素的影响。应用此模型，对焦作市主城区中深层地下水进行了评价，结果表明：该模型应用于地下水水质评价，是合理可行的，且方法简单，便于操作。为水质综合评价提供了新的有效方法。

模糊物元；地下水水质；熵权；海明贴近度

目前，对于地下水水质评价的方法很多，最常用的方法有：BP神经网络、投影寻踪法、模糊综合评价法、灰色系统法和因子分析法等［1］。每种方法有其自身优点和不足。另外，涉及到赋权的问题，即主观赋权法和客观赋权法。主观赋权法反映了决策者的意图，但评价结果具有较强的主观随意性；客观赋权法的评价结果具有一定的理论依据，避免了人为因素带来的偏差。地下水环境是一个较为复杂的系统，有时单项指标间的评价结果往往是不相容的，而物元分析理论［2］主要研究事物的可拓性，并用以解决矛盾问题。物元可拓法的原理是以物元为基元建立物元模型，以物元可拓为依据，应用物元变换化矛盾问题为相容问题。应用熵值法来确定权重系数，避免了权重系数确定的主观性问题。因此，本文将模糊物元与熵权结合起来，构建模糊物元分析模型对地下水水质进行评价。

1 模糊物元评价模型

1.1 模糊物元与复合模糊物元［3］

给定事物的名称N，它关于特征c有量值为v，以有序三元R＝（N，c，v）组作为描述事物的基本元，简称物元。其中，量值v具有模糊性，便称为模糊物元。如果事物N有n个特征c1，c2，…，cn和相应的模糊量值v1，v2，…，vn，称R为n维模糊物元，简记为R＝（N，c，v）。如果m个事物的n维物元组合在一起，使构成m个事物n维复合物元Rmn。若将Rmn的量值改写为模糊物元量值，称为m个事物n维复合模糊物元，记作

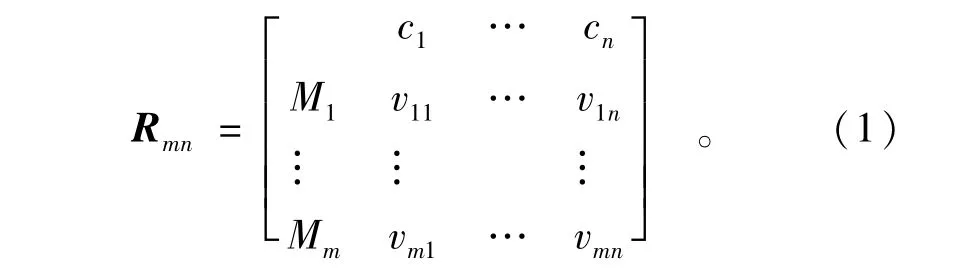
式中：Rmn为m个事物n维复合模糊物元；Mi为第i个事物（i＝1，2，…，m），cj为第j项特征（j＝1，2，…，n）；uij为第i个事物第j项特征对应的模糊量值，即隶属度。

1.2 水质评价的隶属函数

在对某个水样进行等级评价时，将评价的等级作为物元的事物，在此基础上构造复合模糊物元矩阵。为了建立比较优化的标准，需制定一个原则，这个原则就是以单项特征的从优隶属度作为标准来衡量，可称单项从优隶属度原则。所谓从优隶属度［4］，就是各单项特征相应的模糊量值，从属于标准事物所对应的各个特征的相应模糊量值。

越大越优型指标（正指标）：

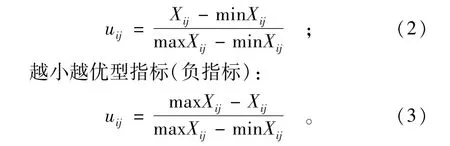
式中：uij为第i个事物第j项特征对应的模糊量值（i＝1，2，…，m；j＝1，2，…，n）；Xij为第i个事物第j项特征对应的量值（i＝1，2，…，m；j＝1，2，…，n；）；max Xij为各事物中第j项特征所对应的所有量值中的最大值；min Xij为各事物中第j项特征所对应的所有量值中的最小值。由此构建隶属度模糊物元

1.3 关联函数和海明贴近度

关联度指两事物间关联大小的量度［4］，表示关联度的函数即为关联函数。解决不同的问题，选择关联函数是不同的，到底选择哪种形式的关联函数，具体问题应具体分析。本文将采用海明距离作为关联函数，利用它衡量某一物元与理想物元接近程度的尺度。之所以选择海明距离，出于这样的考虑：海明距离不仅计算简单方便，而且还克服了加权平均模型的评价值趋于均化的缺点［5］。

海明贴近度计算公式：

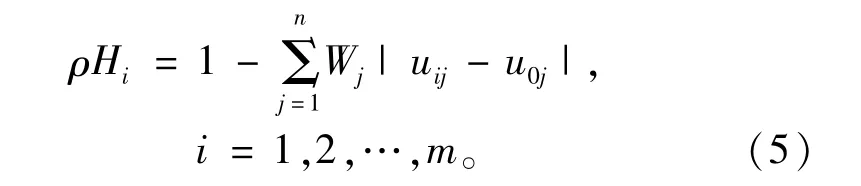
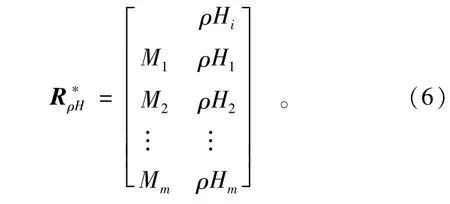
海明贴近度表示各事物与标准事物之间的贴近程度，可以根据贴近度的大小对各事物进行排序，也可进行分类。

2 熵值法确定权重

根据信息熵的定义［6］Hj＝－，说明信息熵是系统无序程度的度量，信息是系统有序程度的度量。某项指标的指标值变异程度越大，信息熵越小，该指标提供的信息量越大，该指标的权重也应越大；反之，某项指标的指标值变异程度越小，信息熵越大，该指标提供的信息量越小，该指标的权重也越小。所以，可以根据各指标指标值的变异程度，利用信息熵计算出各指标的权重。

（1）将各指标标准化，计算第i个样本下第j项指标的比重：

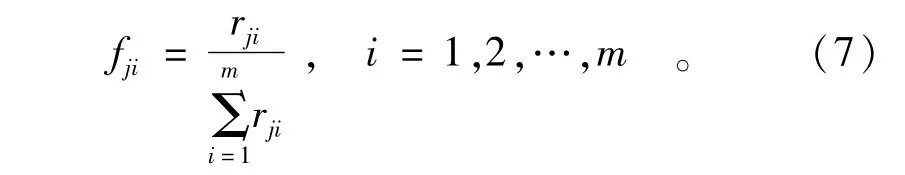
（2）计算第j项指标的熵值：

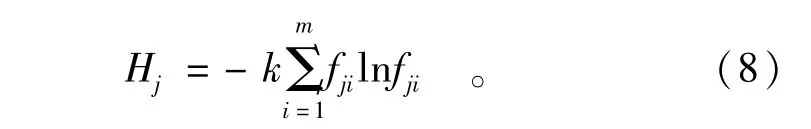
（3）计算第j项指标的熵权：

本文结合水质评价的实际情况，对该法加以修正［7］：式（8）中假定fji＝0时，fjiln fji＝0，那么当fji＝1时，fjiln fji也为0，这显然是不符合实际的。所以对式（7）修正为

3 应用实例

本文以焦作市主城区地下水质评价为例，选取比较有代表性的陶三厂家属院、墙南村、朱村乡政府、中站区烧碱厂等12个监测井，采用《中华人民共和国地下水质量标准》（GB／T14848－1993）作为评价的标准，将水质级别划分为5级（见表1），结合焦作市城区监测井实际监测指标，选取pH值、总硬度、硫酸盐、氯化物、高锰酸盐指数、氨氮、氟化物7项指标作为评价因素。

3.1 建立评价模型

3.1.1 构建复合模糊物元

根据实测数据，对12个监测井和5个分级标准建立17个样本和7个指标的复合模糊物元。

3.1.2 构建隶属度模糊物元

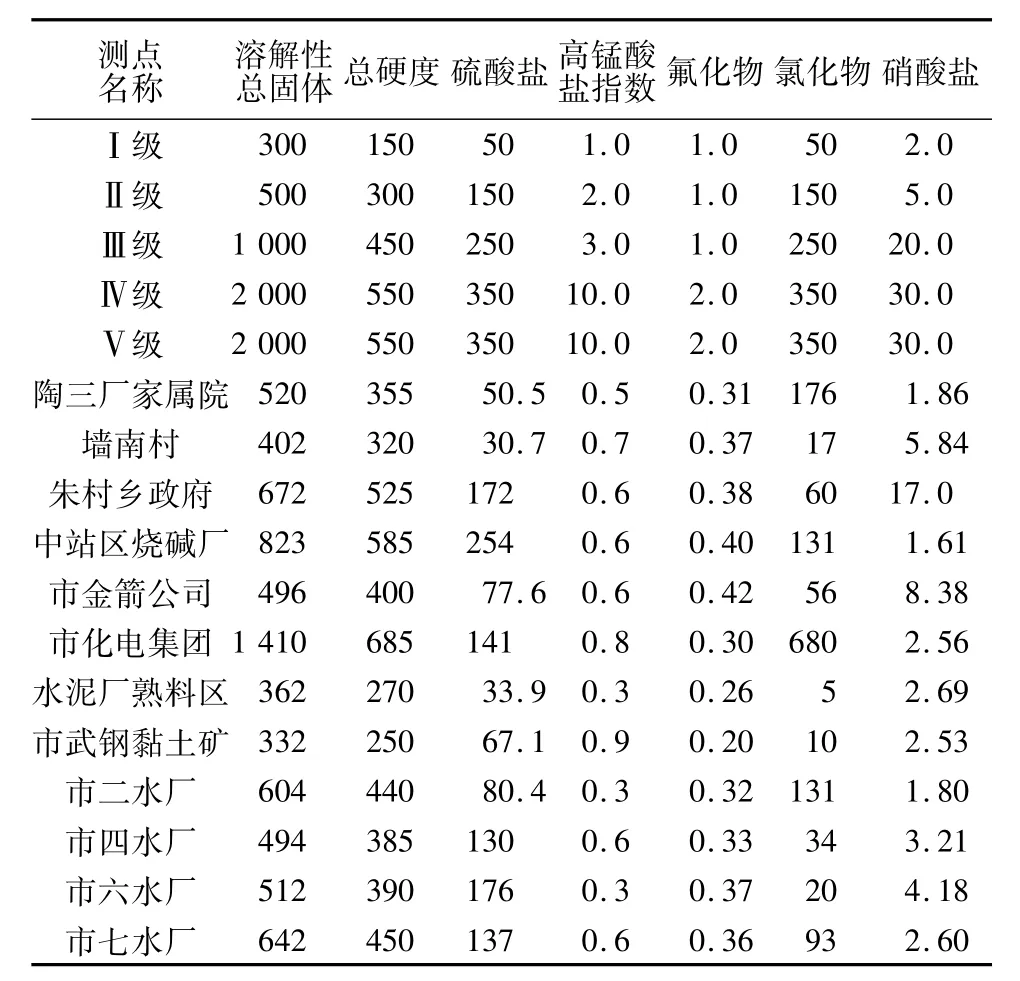
表1 评价指标在12个监测井的实际监测值及分级评价标准Table1 Evaluation index values ofmonitoring items for twelve wells and standard of classification evaluation mg／L

3.1.3 用熵值法计算各指标的权重

（1）各指标进行标准化处理得判断矩阵Rij；

（2）根据公式（7）和（8）计算各指标的熵（为书写方便，写成如下形式）：

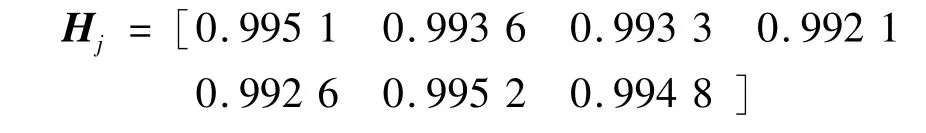
（3）由公式（9）得出各指标权重（为书写方便，写成如下形式）：

3.1.4 海明贴近度的计算

由公式（5）（6）计算出海明贴近度（为书写方便，写成如下形式）：

4 结果分析

经过计算得出各水质监测点的评价结果，由海明贴近度的含义可以得出各样本的评价级别。另外，根据模糊综合评价法，采用加权平均模型——M（·，＋）进行计算，得出的结果与模糊物元评价法得出的结果对比，如表2。

表2 评价结果对照表Table2 Contrast of evaluation results

本次选择的12个监测井7个指标的实测数据，代表焦作市中深层地下水，评价结果表明：50%属于Ⅰ级，50%属于Ⅱ级或Ⅲ级，说明焦作市中深层地下水水质良好，还没有受到更多的污染。尤其水泥厂熟料区、陶三厂家属院等地，属于岩溶水的补给区，含水层为奥陶系灰岩，水量较丰富，水质好，埋深较大，不易污染。中站区烧碱厂、朱村乡政府等地位于市区中下游，水质一般，且已形成降落漏斗。市化电集团位于山前冲洪积扇地带，孔隙水较为丰富，属于浅层水重点开采区，降落漏斗不断增加，水质有明显下降的趋势。

另外，从表2可以看出，模糊物元法与模糊综合评价法相比，二者的计算结果基本一致，但与模糊综合评价法相比，模糊物元法更有其优越性。首先这种方法简单便于操作，采用贴近度的思想，并结合熵权的应用，避免了主观人为因素的影响，结果更真实可信，而且对于水质评价中的不相容性和模糊性也得到了很好的解决。

［1］ 厉艳君，杨木壮.地下水水质评价方法综述［J］.地下水，2007，29（5）：19－20.（LI Yan-jun，YANG Muzhuang.A review of groundwater quality evaluationmethods［J］.Groundwater，2007，29（5）：19－20.（in Chinese））

［2］ 蔡 文.物元模型及应用［M］.北京：科学技术文献出版社，1994：25－28.（CAIWen.Matter Element Model Analysis and Application［M］.Beijing：Science Press，1994：25－28.（in Chinese））

［3］ 张 斌，雍歧东，肖芳淳.模糊物元分析［M］.北京：石油工业出版社，1997：8－9.（ZHANG Bin，YONG Qidong，XIAO Fang-chun.Fuzzy Matter-Element Analysis［M］.Beijing：Petroleum Industry Press，1997：8－9.（in Chinese））

［4］ 张海涛，雷小东，张 芳，等.灰色关联度法在盘锦市曙光地区地下水水质评价中的应用［J］.世界地质，2005，（1）：68－71.（ZHANG Hai-tao，LEI Xiao-dong，ZHANG Fang，et al.Application of ray related degree method in groundwater quality evaluation of Shuguang Area of Panjin city［J］.TheWorld Geological，2005，（1）：68－71.（in Chinese））

［5］ 祁兴会，陈晓楠.基于三标度法的模糊物元模型在湖泊水质评价中的应用［J］.节水灌溉，2007，（7）：38－39.（QIXing-hui，CHEN Xiao-nan.Application of fuzzy matter elementmodel based on Threemark Method in the evaluation ofwater quality of lake［J］.Water-saving Irrigation，2007，（7）：38－39.（in Chinese））

［6］ 邱菀华.管理决策与应用熵学［M］.北京：机械工业出版社，2002：193－199.（QIU Wan-hua.Management of Decision-Making and Application of Entropy-Learning［M］.Beijing：Mechanical Industry Press，2002：193－ 199.（in Chinese））

［7］ 周振民，常 慧.基于熵权的模糊物元地下水水质评价模型［J］.中国农村水利水电，2008，（12）：46－47.（ZHOU Zhen-min，CHANG Hui.Based on entropy of fuzzymatter-elementmodel of groundwater quality assessment［J］.Chinese RuralWater and Hydropower，2008，（12）：46－47.（in Chinese） ）

（编辑：曾小汉）

Application of Fuzzy M atter-element M odel in Groundwater Quality Evaluation

ZHANG Jun-hua1，YANG Yao-hong2，CHEN Nan-xiang1
（1.Resources＆Environment Institute，North China University ofWater Conservancy and Electric Power，Zhengzhou 450011，China；2.Water Conservancy Institute，North China University of Water Conservancy and Electric Power，Zhengzhou 450011，China）

On the basis of fuzzymatter-element analysis and in combination with entropy weights，amatter-element modelwas established to evaluate groundwater quality.Regarding thewater quality level as the object ofmatter-element，and constructing the compound fuzzy matter-element through various evaluation indexes and corresponding fuzzy values，the water quality evaluation was achieved through calculating Hamming approach degree between the fuzzy matter-elementand the standard fuzzymatter-element.Adopting the entropymethod to determine weights，the man-made effectmay be avoided.Themodelwas applied to evaluate themiddle-deep level groundwater quality of Jiaozuomain city area.The results show that applying themodel to evaluate groundwater quality is reasonable and feasible and the approach is simple and convenient to operate.The paper provides a new effectivemethod for the comprehensive evaluation of water quality.

fuzzymatter-element；groundwater quality；entropy weight；Hamming approach degree

TV211.1

A

1001－5485（2010）09－0010－04

2010-03-02；

2010-08-01

张俊华（1973-），女，内蒙赤峰人，讲师，主要从事水资源管理及生态环境建设方面的教学和研究，（电话）13373921520，0371-69127351（电子信箱）junhua20081973＠126.com。