压痕应变法测量残余应力的不确定度分析

陈怀宁，胡凯雄，吴昌忠

（中国科学院金属研究所，辽宁 沈阳 110016）

1 引 言

目前，利用球形压痕周围弹性应变场的变化信息求取构件内部（残余）应力场的方法——压痕应变法，正以其独特的便携性和快捷性、极小的表面破坏性、高的灵敏度和重复性而得到关注。该方法不同于利用宏观压痕诱导的维氏硬度或纳米压痕产生的载荷-深度曲线的变化信息来求解残余应力[1-2]，而是通过事先布置在压痕附近的位移敏感元件（如应变片）来获知原始应力的大小[3-8]。图1为该方法的测试过程示意图，图2为该方法的测试原理说明图。

但是，不管仪器设备多么先进，测量方法如何完善，技术人员水平有多高，各种检测结果始终存在着误差。由于误差的客观存在，检测结果也必然存在着测量的不确定度。确切描述测量结果不确定性的参量就是“测量不确定度”（Uncertainty in Measurement）。1993年国际不确定度工作组制定并于1995年修订的《测量不确定度表示指南》（简称GUM）由ISO出版，GUM的问世推动了测量不确定度在世界范围的应用。我国1999年原则上等同采用GUM发布了JJF 1059-1999《测量不确定度评定与表示》计量技术规范，使我国测量不确定度的应用得到了空前发展[9]。

2 测量条件

应力测量标准依据《金属材料压痕应变法残余应力测量》国家标准（报批稿）进行，测量环境温度0℃～40℃，湿度正常，材料为一般钢铁材料，典型牌号为Q345低合金钢。选用设备为KJS-2压痕应力测试仪，应变片为BA120-1BA-ZKY双向箔式应变花，压痕形成装置为φ1.588mm的压头和弹簧冲击加载方式。

3 数学模型及来源分析[5]

采用压痕应变法测量残余应力时，首先是通过测得的应变增量 Δεx，y计算残余弹性应变 εx，y：

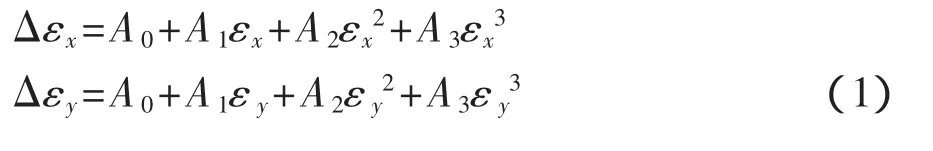
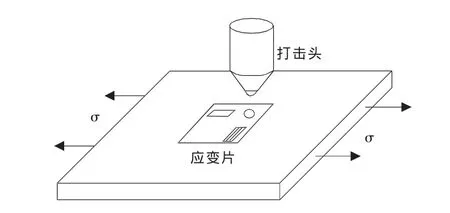
图1 压痕应变法测量应力示意图

图2 压痕应变法测量应力原理图

式中：Δε——称为应变增量，压痕诱导下的应变输出值，单位με；

εx——X方向的残余弹性应变计算值，单位με；

εy——Y方向的残余弹性应变计算值，单位με。

研究表明，将式（1）按式（2）进行分段线性简化，一般可以得到非常接近的结果：

获得弹性应变εx，y后，利用Hooke定律计算双向残余应力：

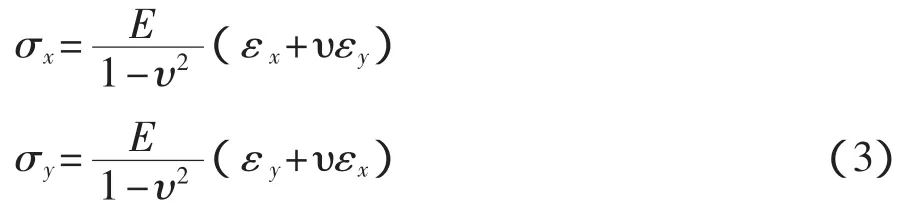
式中：E——弹性模量，材料常数，低合金钢取210GPa；

υ——泊松比，材料常数，一般金属材料取0.285。

应力测量结果的不确定度来源分析见图3。其中重复性误差受到的影响因素较多，各影响因素的作用如下：（1）打击能量的变化很小，主要由弹簧抗力、压头自重（对不同打击方向有影响）、滑道摩擦力等决定。（2）按相应国标生产的钢球直径变化很小。（3）片基厚度一般在0.04～0.05mm，同批次生产的厚度基本不变。（4）俗称502胶的氰基丙烯酸酯胶层厚度一般在0.01～0.05mm，在此厚度范围内胶层对应变传递的影响不大，而需要避免的是粘接剂失效的情况。（5）贴片质量主要受应变栅中心线与主应力方向之差、粘接剂厚度是否为0等因素影响。已有研究表明，贴片角度在±15°内对应变增量的大小影响不大，而应变增量和残余弹性应变之间的关系始终保持不变。当应变片下方无胶层时，应判此片作废，数据不可采用。（6）表面状态包括砂轮打磨和清洁程度，表面打磨操作不当时可能会引入新的残余应力，但如果采用相近的打磨工艺，并保证砂轮粗磨时金属表面不变颜色，经过抛光后的表面状态认为是一样的。至于表面清洁程度，需要满足贴片要求，否则应判废。（7）压痕对中的精度一般由设备保证。研究表明对中偏差只要不超过0.05mm，应变输出变化可以忽略，而设备自身的精度要求是0.02mm，故此项可以忽略。

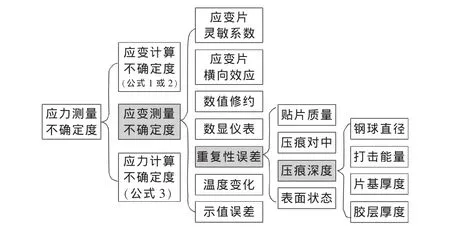
图3 压痕应变法测量残余应力过程中不确定度影响因素

综上，影响压痕应变法测量残余应力重复性误差的因素有的可以忽略，不能忽略的如果难以独立进行测量不确定度评价，可以通过系列试验，以一个应变测量的重复性误差方式集中表现出来。

4 不确定度分量的计算[10]

以下评定一般按B类评定不确定度，除非必要，变量一般按均匀分布考虑。B类不确定度的评定，一般根据经验和资料，分析判断被测量值x的可能值y的区间（-a，a），并假定被测量值的概率分布，由要求的置信水平（即包含概率）选取对应的包含因子k，则其测量不确定度为U（x）=a/k，a为区间半宽度。

包含因子k的值是根据y±U的区间要求的置信水平选择的，一般k在2～3范围内。当置信水平要求达到95%时，k=2；当置信水平高达99%时，k=3。美国NIST和欧洲WECC的方针都是在一般情况下取k=2。必要时也可根据假设的概率分布选取相应的k值。

如果假设应变测量某环节的可能值为正态分布，当具有置信水平95%时，k=1.96。

4.1 数显仪表的应变不确定度uε（ε）

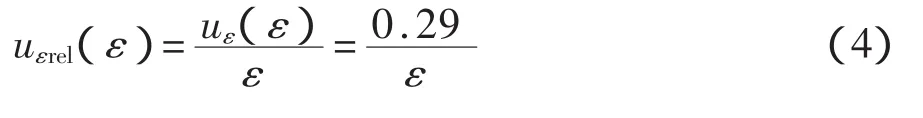
4.2 重复性试验的应变不确定度ur（ε）

如上所述，重复性试验的误差包括很多因素，在相同测量条件下，经验表明，两次测量结果之差的重复性误差限r为±20με，k值按反正弦类型分布，有：

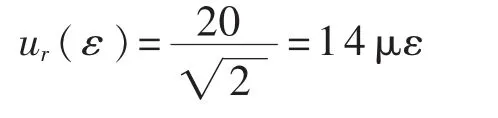
相对标准不确定度为：

4.3 应变仪示值误差引起的不确定度uM（ε）

按照最低应变仪的精度要求，示值误差按±1%计算，则相对不确定度：

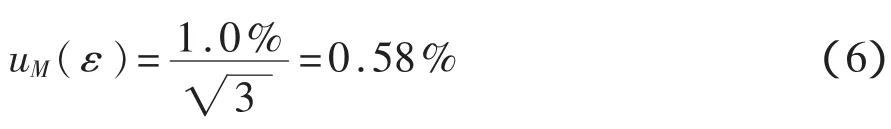
4.4 温度变化引起的不确定度uT（ε）

因为应变测量采用自补偿方式，加上测量一般在室温条件下进行，因而温度效应可以得到很好的控制，此时应变片温度效应引起的误差限可取±5με，则标准不确定度uT（ε）为：

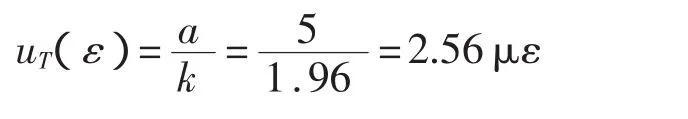
相对标准不确定度为：

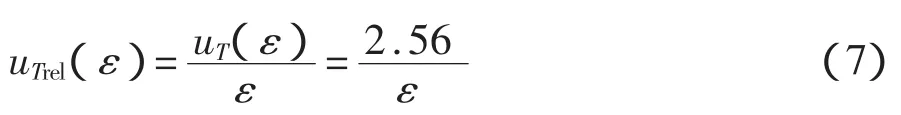
4.5 应变片灵敏系数的不确定度uk（ε）

由应变片BA120-1BA-ZKY的包装盒信息可知，其灵敏系数k=2.04×（1±1%），1%为灵敏系数平均值的相对标准偏差，因此灵敏系数的相对标准不确定度为1%，即：

4.6 应变片横向效应引起的不确定度uF（ε）

由应变片使用说明书可以查得应变片的横向效应引起的应变测量相当误差限为±1%，因此，测量不确定度为：

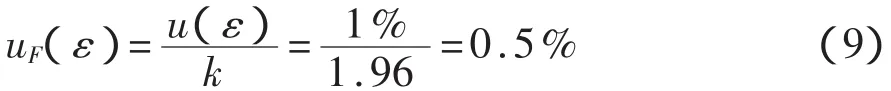
4.7 应变片方向偏差引起的标准不确定度u0（ε）

虽然已知贴片方向（同主应力或焊缝方向），但贴片操作并不能完全保证应变栅轴线与之完全平行或垂直，故可能引起一定的误差，根据有关资料，相当误差限为1%，则相对标准不确定度为：

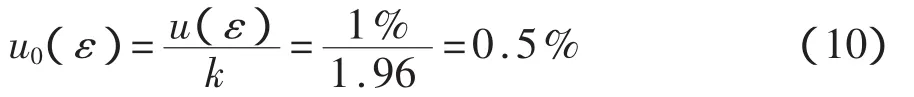
4.8 零点漂移引起的不确定度

如果系统的零点漂移满足相应标准，即在4 h内应变变化数值不大于±3με，而压痕应变法的应变测量间隔可在1min内完成，因而由零点漂移引起的数据误差可以忽略。

4.9 导线电阻引起的误差uΩ（ε）

测量系统中导线的长度一般为3m，其总电阻r为0.2 Ω，测量用应变片的电阻R为120 Ω，按照半桥方式连线，则应变读数相对误差：

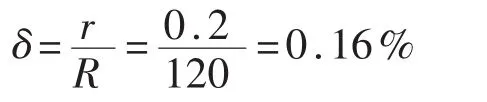
相对标准不确定度为：

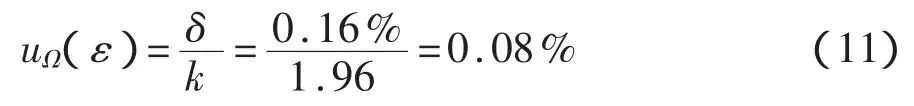
5 合成标准不确定度

（1）根据B类评定的有关公式，应变增量的合成标准不确定度 u（Δε）为：

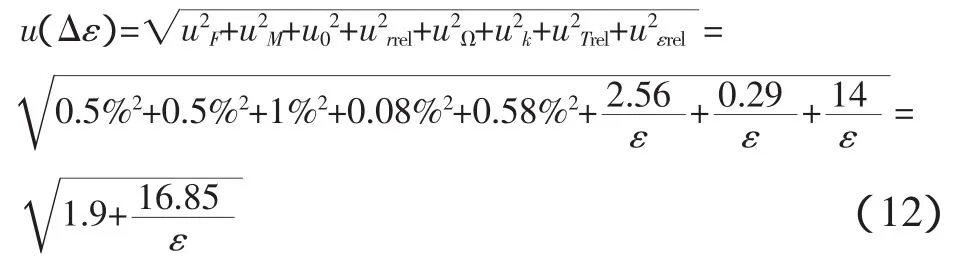
由式（2）可知，Δε和ε的关系互为线性关系，但系数要发生变化。因此，由应变增量的合成标准不确定度u（Δε）可得弹性应变的合成标准不确定度 u（ε）如下：

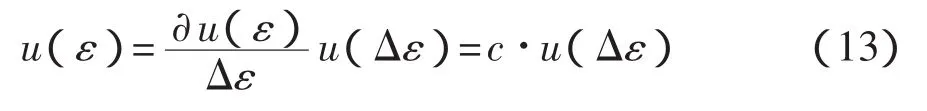
（2）应力不确定度

（a）数值修约引起的不确定度uσ（σ）

应力数值的单位为MPa，修约到个位，则：

（b）弹性模量E引起的不确定度u（E）

式（3）中的E值不确定度有时不能忽略，因为不锈钢的E值范围为185～195GPa，合金钢的E值范围为200～210GPa，若不能知道E的确切数值而采用估计数值计算时，则有可能产生约±5%的误差，故：

（c）泊松比引起的不确定度

在材料的弹性应力测量中，一般认为υ的精确值为0.285，即使近似将υ取值0.3（增大约3%），对于（1-υ2）来说，其相对误差也仅有（0.32-0.2852）/（1-0.2852）=0.96%。此外，若考虑υ值的影响，将给应力不确定度的计算带来很大的困难，因此这里忽略υ的不确定度影响，即将υ视为常数。

（d）应力计算引起的不确定度

综上，应力计算引起的不确定度由应变测量的不确定度根据以下传递公式计算得到：

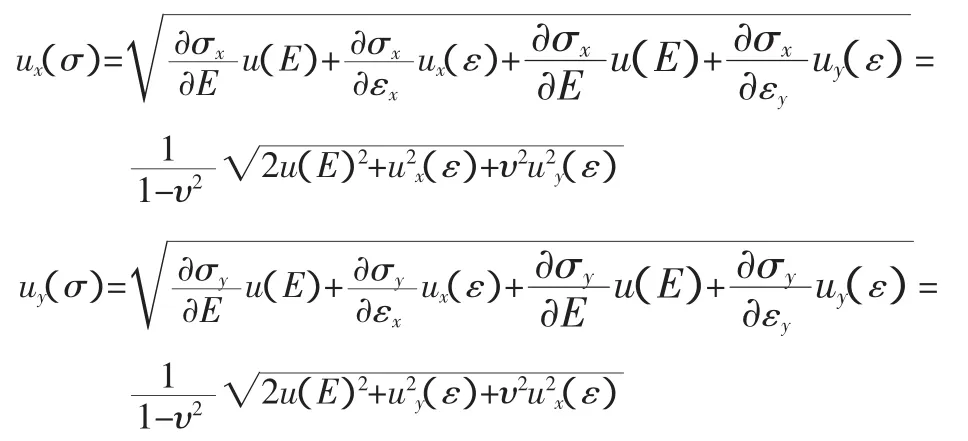
带入数据后得到：

6 扩展不确定度U

取包含因子k=2，则：

7 模拟分析

以上计算表明，扩展不确定度的大小与所测应变的绝对值有直接关系，为此计算了压痕应变法测量Q345材料焊接残余应力过程中的几种典型值的相对不确定度，结果列于表1。为计算方便，在计算U值时忽略了贡献率很小的uσ（σ）分量影响。前述式（2）的实际标定结果为：

当应力小于0.6屈服强度时：

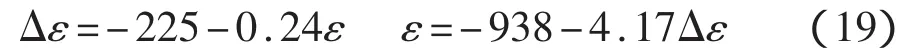
当应力大于0.6屈服强度时：

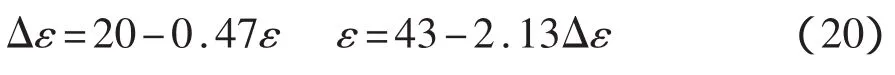
利用式（12）～（13）和式（16）～（18），得到表1结果，表中Urel（σ）为不考虑弹性模量E不确定度影响时（即已知E值）的应力相对不确定度。

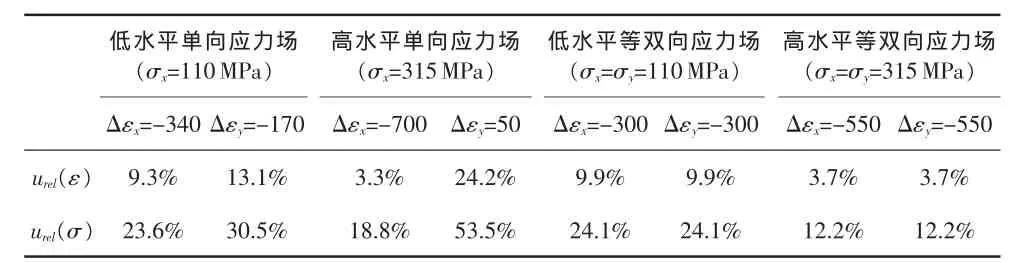
表1各种应力水平下的不确定度分析结果

8 结束语

（1）应力相对不确定度的大小主要取决于应变绝对值的大小，除单向高值应力场外，两者的关系为：

Urel（σ）≈2[urel（ε）+2.3%]

（2）低应变情况下相对不确定度的大小主要由重复性试验的应变不确定度ur（ε）决定，该应变值与重复性误差限（±20 με）越接近，相对不确定度的值越大。

（3）虽然相对不确定度与原始应力（应变）大小有关，但标准不确定度数值应是相近的，即均在20～30MPa范围（单向高值应力场情况除外）。

（4）除了高值双向应力场外，弹性模量E的误差对应力不确定度的影响较小。

[1] Frankel J，Abbate A，Scholz W.The effect of residual stresses on hardness measurements [J].Experimental Mechanics，1993（33）：164-168.

[2] Swadener J G，Pharr G M，Taljat B.Measurement of residual stress by load and depth sensing indentation with spherical indenters[J].J.Mater.Res.，2001，16（7）：2 091-2102.

[3] Underwood D.Residual-stress measurement using surface displacements around an indentation [J].Experimental Mechanics，1972，13（9）：373-380.

[4] 陈亮山，董秀中，潘 兴.冲击压痕测定残余应力研究[C]∥第七届全国焊接学术会议论文集（5）.青岛：中国机械工程学会焊接学会，1993：21-24.

[5] 孟宪陆，陈怀宁，林泉洪，等.压痕应变法中压痕周围的应力应变分布规律[J].焊接学报，2008，29（3）：109-112.

[6] 陈怀宁，陈 静.压痕应变法应力测量中双向应变增量的变化规律[C]∥轻金属焊接关键基础研究.西安：中青年学者学术论坛，2008.

[7] 曲鹏程，陈怀宁，林泉洪，等.屈服强度对压痕应变法测量焊接应力中应变增量的影响[J].机械强度，2007，29（6）：904-907.

[8] 林丽华，陈立功，顾明元.球面压痕测残余应力试验方法研究[J]，机械强度，1998，20（2）：303-307.

[9]中国合格评定国家认可中心，宝山钢铁股份有限公司研究院.材料理化检验测量不确定度评估指南及实例（CNAS-GL10：2006）[M].北京:中国计量出版社，2007.

[10]杜雅飞，高柄军，张及瑞.内压球壳大开孔接管区电阻应变测量中不确定度的评定[J].中国测试技术，2004，30（5）：23-25.