高速列车湍流特性的数值模拟

2010-08-08张军海王吉桥吴向东扶原放

铁道机车车辆 2010年1期

张军海,王吉桥,吴向东,扶原放

(1 西南交通大学机械工程学院,四川成都610031;2 山东威海市地方铁路管理局,山东威海264200;3 吉林大学汽车工程学院,吉林长春130025)

列车外流场的分析有在线实车试验、风洞试验、解析解法、列车动模型试验、数值模拟等方法,目前CFD方法已经能够准确模拟出任意时刻流场中任意点的流动,研究周期短、费用低,与各种模型试验相比有其优越性[1-3]。本文用FLUENT软件对列车外流场进行模拟,采用了4种常用的湍流模型,给出了受力、速度和压力分布情况,并对分析结果进行对比分析。

1 流体力学的基本方程

列车运行引起的空气流动,是一种不可压缩、存在边界层分离的三维定常紊流流动,它遵守质量守恒、动量守恒和能量守恒定律[1]。流体动力学控制方程就是根据流体的连续介质假设,由以上定律出发推导出的描述流体运动基本规律的数学表达式。

质量守恒方程:

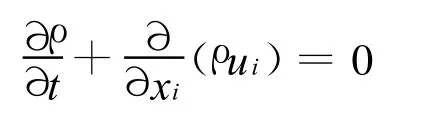
动量守恒方程:

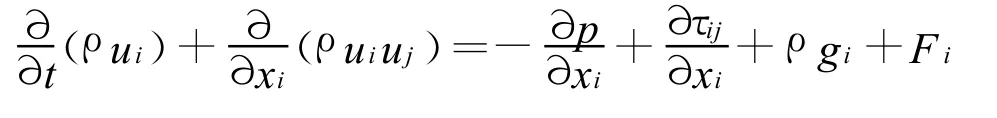
能量守恒方程:

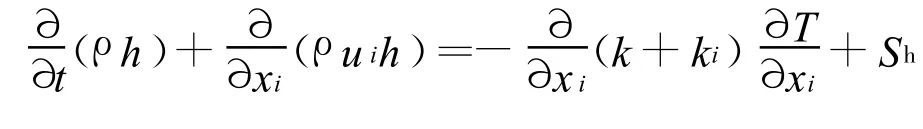
2 常用湍流模型

2.1 标准k-ε模型

标准k-ε模型是一种涡黏性模型,它和代数模型的主要差别是湍流涡黏性系数μt包含了部分历史效应,将湍流黏性系数和湍流动能及其耗散率联系在一起[2]:

式中Cμ是湍流常数,一般情况下取Cμ=0.09;k是湍流动能;ε是湍流耗散率。

标准k-ε模型的湍流动能k和耗散率ε方程如下:

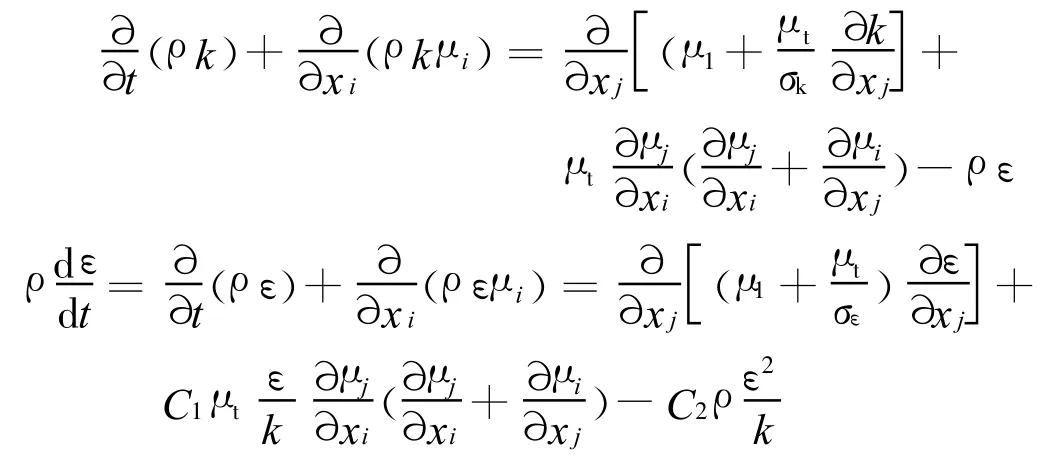
式中 μ1是层流黏性系数;C k、C2、σk 和 σε是经验常数,一般取值[2]如下:Ck=1.47,C2=1.92,σk=1,σε=1.33。

标准k-ε模型假定黏度系数是各向同性的,不能反映各向异性,并且是针对发展非常充分的湍流流动来建立的,是一种高雷诺数湍流计算模型,在列车表面雷诺数比较低,湍流发展不充分,计算会出现失真。下面介绍标准k-ε模型的两种改进形式,RNGk-ε模型和可实现k-ε模型。

2.2 RNGk-ε模型

在RNGk-ε模型中,通过在大尺度运动和修正后的黏度项体现小尺度的影响,使这些小尺度运动有系统地从控制方程中去除[1],由此得到k方程和ε方程如下:

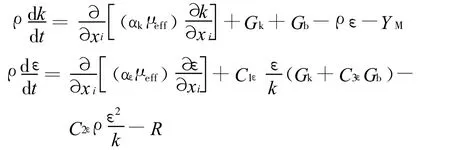
式中αk和αε分别是湍流动能k和耗散率ε的有效湍流普朗特数的倒数。μeff=μ+μt。RNG k-ε模型修正了湍流动能黏度,引入了与旋转和曲率有关的内容,改进了ε方程,能更好的处理高应变率及流线弯曲程度较大的流动,对近壁区和低雷诺数的流动都能进行很好的计算[1]。

2.3 可实现k-ε模型

可实现k-ε模型的湍流动能k和耗散率ε的方程为:

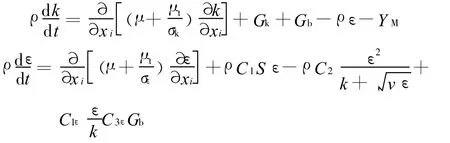
图1 列车头部局部网格放大图

2.4 标准k-ω模型

标准k-ω模型是一种经验模型,是基于湍流能量方程和扩散速率方程,k方程和ω方程如下:

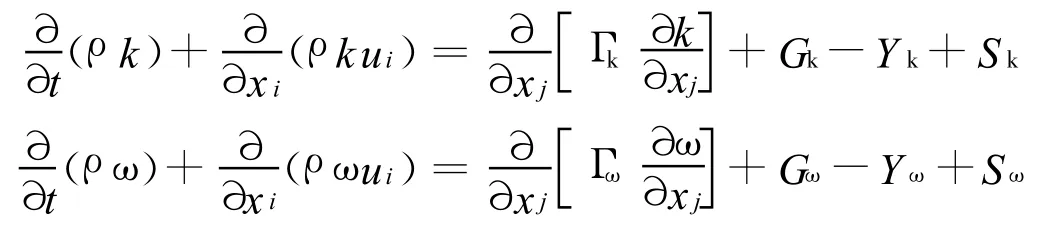
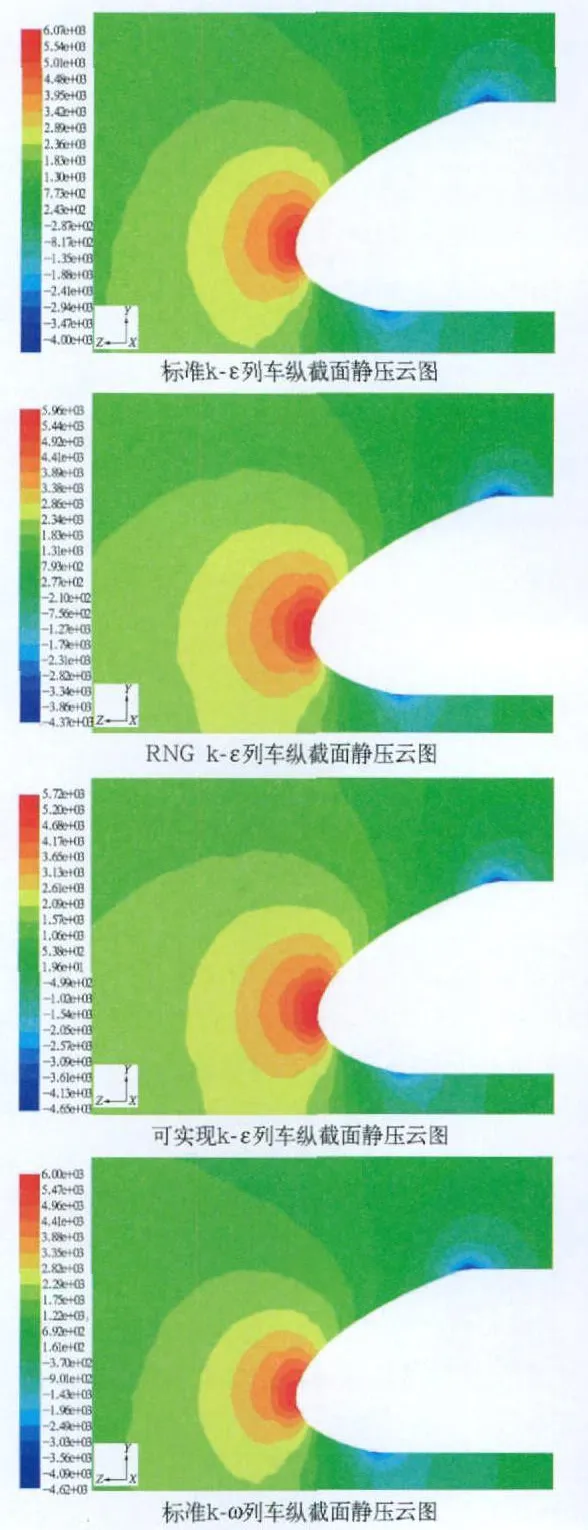
图2 列车纵截面压力云图(Pa)

式中Gk是由层流速度梯度而产生的湍流动能。Gω是由ω方程产生的,代表ω方程。Γk和 Γω表明了k和ω的扩散率。Y k和Yω由于扩散产生的湍流。标准 k-ω模型中包含了低雷诺数影响、可压缩性影响和剪切流扩散,因此适于尾迹流动计算、混合层计算、射流计算,以及受到壁面限制的流动计算和自由剪切流的计算。

3 计算模型的建立

选用PRO-E建立1∶1模型,模型长约28m,对列车表面作了相应的简化,去掉了受电弓、车轮、刮雨器等突出部件,并对列车表面作了光滑处理。模型计算区域范围头部区域是车高的3倍,尾流区域为车高的10倍[3],计算区域为80 m×12 m×12 m。网格划分选用ICEM CFD软件,网格类型选用4面体网格,4面体网格有很好的适应性,特别是对复杂外形的模型很适用[4](图1)。

4 数值模拟计算结果与分析

高速列车速度取300 km/h,对应马赫数Ma＜0.3,列车绕流问题可作为黏性不可压缩定常流动处理[5]。又由于流场雷诺数Re＞106,为紊态流动,故采用k-ε模型和标准k-ω模型进行模拟。

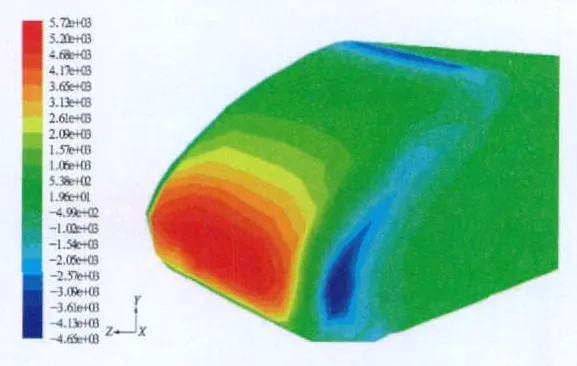
图3 列车头部表面压力分布(Pa)

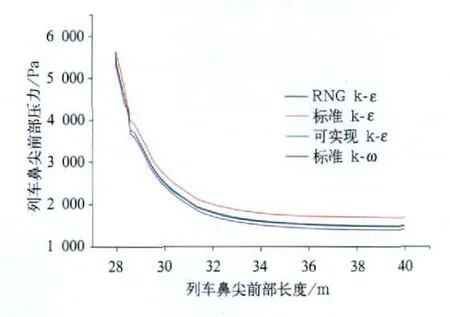
图4 列车鼻尖前部压力

图5 不同速度下的云图/(m◦s-1)

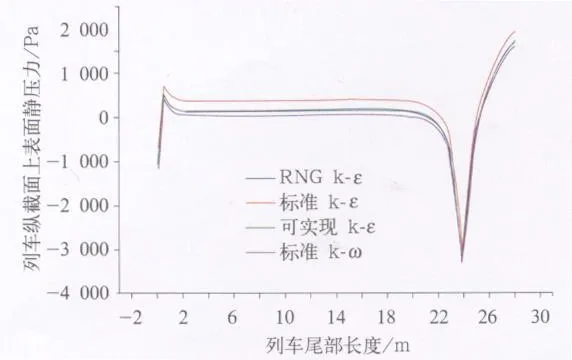
图6 列车纵截面上表面压力曲线

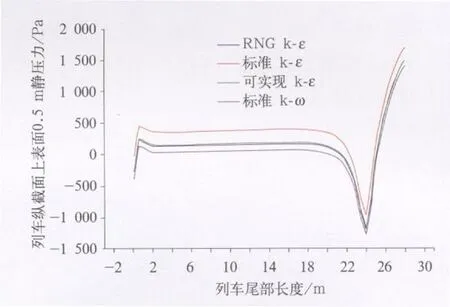
图7 列车纵截面上表面0.5m压力曲线

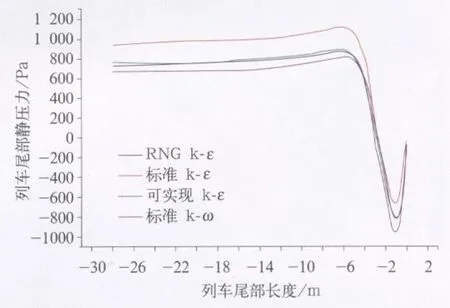
图8 列车尾部压力曲线

图9 列车尾部速度曲线

列车在前行时将前方静止气流排开,空气被压缩,形成正压区,且形成较大的压力梯度,鼻尖部正压最大,气流经过列车头部向上、下及侧面过渡时发生分离,在转折处形成负高压区[6,7]。图2为列车纵截面压力云图,从图中可以看出在列车前部产生较大的正压,由于选用的湍流模型不同,列车前部的正压区域大小不同,最大正压值也不同。图3是列车前部压力分布图,列车鼻尖位于最大正压区,列车前端面向车身过渡曲面位于最大负压区,最大正压值和最大负压值见表1。图4是列车鼻尖前部压力,可以看出RNG k-ε模型下的压力分布区域最大,标准k-ε模型和可实现k-ε模型次之,变化曲线相似,标准k-ω模型最小。

从图3和图5可以看出,在列车前端面向车身过渡处,气流发生分离。标准k-ε模型假设流动为完全湍流,忽略分子黏性的影响,而列车表面处由于黏性作用力使湍流发展并不充分,因此计算会产生失真,在曲面过渡处及上下表面近壁区低雷诺数情况下表现不是很好,经过改进的RNG k-ε和可实现k-ε能达到好的效果,计算结果更接近真实值,符合计算要求。

表1 列车压力值

图6和图7是列车纵截面上表面及0.5m处压力曲线。RNG k-ε模型经过改进可以更好的计算列车近壁区和低雷诺数的流动,标准k-ε模型由于条件限制只能模拟湍流充分发展的流动,因此RNG k-ε模型下列车表面的压力最大,标准k-ε模型在列车壁面区模拟时会因为低雷诺数而失真,在贴体表面处压力最小,可以得出标准k-ε模型对于壁面区的处理不是很好,应同时用壁面函数法对近壁区进行处理。

图5可以看出,列车在前沿转折处附面层气流分离,速度下降,到达尾部转折处气流二次分离后进入尾流区,产生复杂的涡流,在靠近列车尾部处为负压区,气流流动紊乱,远离尾部气流速度逐渐增大,压力也增大直至趋于稳定,由图8压力曲线和图9速度曲线可以看出RNG k-ε模型下压力最大,速度最小,在贴近尾部中心和尾流区各有一旋涡区,此旋涡区为负压区,此处的速度很低,尾部负压区与头部正压区形成压差阻力[8],这也是形成列车阻力的主因。RNG k-ε模型和可实现k-ε模型都能更好的模拟列车尾流,但综合考虑对整个列车流场的模拟,结合本文的对比结果可以得出RNG k-ε模型最适合。