一种基于混沌码的宽间隔跳频图案实现

张 波， 杨光宣， 金炜东， 吴 潜， 苟先太， 肖和飞

（①西南交通大学, 四川 成都 610031；②中国电子科技集团公司第10研究所，四川 成都 610036）

0 引言

混沌扩频通信的研究已取得一些进展，特别是混沌跳频序列的研究，理论分析及数值模拟也证实了混沌序列作为新的跳频序列具有相关性能好、跳频间隔宽、多址容量大、均匀性好、产生速度快、保密性强等优点,它已经逐渐被应用于跳频通信中。文献[1]中提出了对Logistic映射的轨道点进行多值量化产生q元 跳频序列的方法，文献[2]给出了一种减小其汉明相关值的新方法，都有汉明相关较大，迭代次数大等不同缺点，鉴于其两种方式的不足本文提出了直接将小数部分二进制然后按比特抽取与列比特抽取交替的方法，最后在按非线性模D法进行宽间隔处理，使其具有良好的性能。

1 跳频序列产生及宽间隔处理

1.1 基于logistic混沌映射

Logistic满映射:

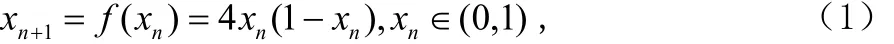
它所产生的混沌序列的不变测度为：

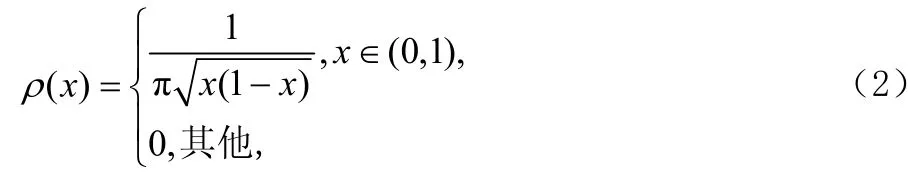
只要选取不同的适当的初始值，经过迭代就可以得到完全不同的混沌序列，因此其数量可以说是无穷的。我们提出从混沌轨道点的二进制数表示式的比特流中，按照顺序来抽取产生跳频序列的新方法，具体方法如下。首先利用Logistic映射产生N个实数值序列元素nx，表示成二进制序列：

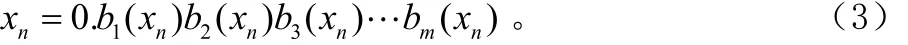
若要产生N个q元混沌跳频序列，则必须产生lbNq·个比特数据。

下面阐述本文方法所抽取过程：

先根据调频序列长度N确定和频隙数q，抽取位置J，根据序列长度来确定迭代次数，

迭代次数公式如下：

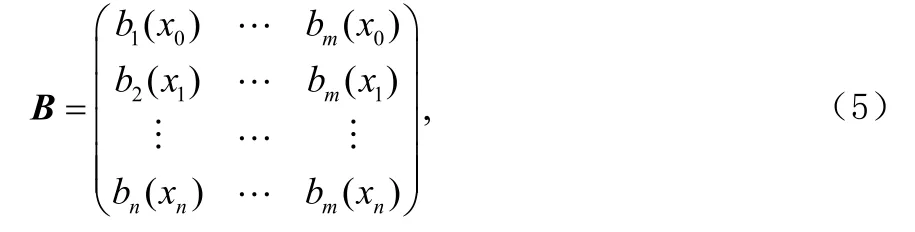
根据迭代次数得如下矩阵：由上迭代所产生的矩阵，我们按列行交替抽取的方法来实现混沌码由实值序列到二进制混沌扩频序列的转化。

先第一序列从上述B中从第一行开始按从给定的列位置J行抽取lbq比特，然后第二序列从矩阵B中依次选取lbq列，从列位置函数给定的J值开始，按列抽取lbq个比特,所产生的矩阵如下所示,这样 1N 和 2N 交替抽取方式 ，产生N个

长度的二进制序列,然后每个序列转化为十进制，则可得跳频长度L=N,频隙数目为q的混沌序列，此方法迭代次数相对于按行单比特抽取的迭代次数大大减少，多于文献[1-2]全按列的方式抽取方式，但其性能得到了显著改善。

1.2 宽间隔处理方法

为克服对偶法这类缺陷本文采用非线性模D法[3]进行宽间隔处理，定义生成频带为m序列的周期,要求满足, 否 则根据跳频间隔的定义,,所以基于m序列利用非连续抽头模型构造宽间隔跳频序列时,d的取值范围是[0,pr-1]。经过这样修正处理后,频域F上确定的频率点就构成了所需要的宽间隔跳频图案。此方法和其他方法[3-5]相比不需要构造对偶频率点,增加了序列的随机性,扩展了频率范围。

2 仿真及分析

首先利用matlab产生不同初值条件下的混沌码序列。本文用上述方法自编函数，其中x0为初值，L为长度,q为元数,j为起始比特抽取位。现取初值产生两组混沌序列:

然后进行非线性模D法宽间隔处理，（由于篇幅所限）未列宽间隔处理后数据。

混沌跳频序列的平衡特性参数：

其中 fi为第i个频隙在一个码周期内出现的次数。显然，在理想条件下，有这时 δ=0。δ越接近 0，则说明该序列的平衡特性越好。

由图1可知，该混沌序列具有较好的平衡特性。汉明自互相关值（由于版面有限）未列出数据，只列出仿真图形如图2，下页图3所示。

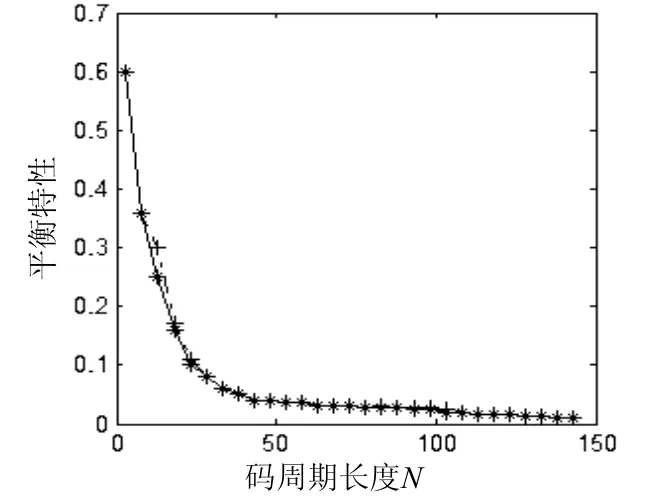
图 1 此混沌码平衡特性

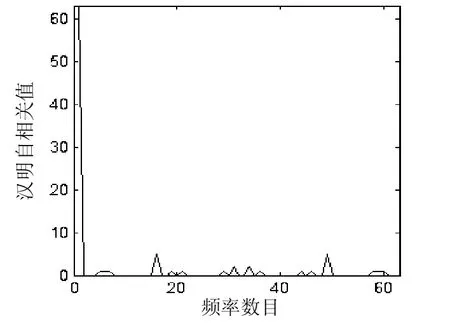
图 2 此混沌码汉明自相关

由图2，下页图3和实验数据分析，虽然其性能与m序列和rs码相比略差，但是在周期较长时其他性能可以很好地弥补这一自身缺憾。

对均匀性的检测采用统计中的2χ检测方法，设跳频序列长度为N,若q个频率点中的第i个频率出现的次数为N，则:

由于混沌系统的确定性，基于相空间重构方法对混沌跳频通信实施预测干扰成为可能。因此，破坏相空间的结构就成为对抗跳频通信预测干扰的一种手段，本文提出的跳频序列构造方法就具有这种能力。如图4，图5按上述所给数据，取j=3时。

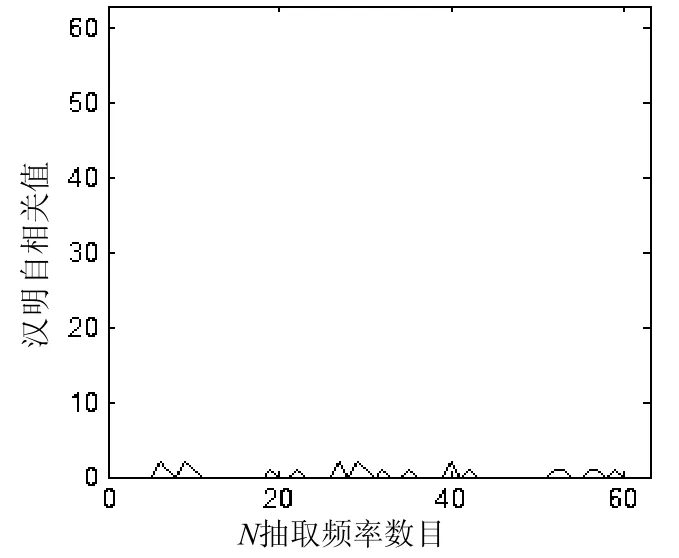
图 3 此混沌码互相关

图 4 此混沌码均匀分布特性

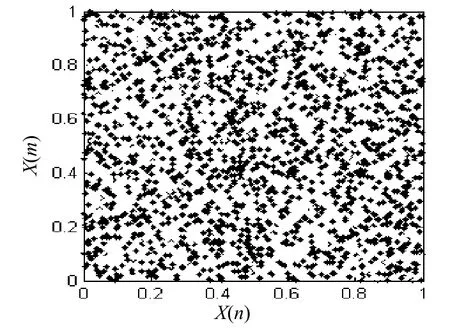
图 5 此混沌码相空间分布

由试验所得可知本文构成的跳频序列相空间分布均匀，不受参数的影响，难以找出特定的规律,究其原因就是本文提出的方法比特抽取和非线性模D相当于多进行了两次次非线性变换，因此具有更好的抗干扰和抗截获性能。

3 结语

本文所用方法理论分析和统计性能实验表明，在相同的条件下该跳频序列采用的按列行交替抽取的方法来实现混沌码由实值序列到二进制混沌扩频序列的转化方法，和基于非线性模D法两次非线性处理方式极大地增加了其平衡性、跳频间隔和最大汉明相关值与线性复杂度，均匀分布特性，而且非线性变换[6-9]极大地增大了抗截获抗，抗干扰能力，这种方式的处理对于保密通信、航天遥测、遥控、测距系统、跳频多址通信的应用的非常适用。

[1] 凌聪,孙松庚.Logistic映射跳频序列[J].电子学报1997,25(10):79-81.

[2] 凌聪,孙松庚.用于跳频码分多址通信的混沌跳频序列[J].电子学报,1999,27(0l):67-69.

[3] 李金涛，汪晓宁，王祎，等.基于m序列的宽间隔跳频序列的生成[J].电讯技术,2007,47(03):36-40.

[4] 甘良才,吴燕翔.基于混沌的宽间隔跳频序列[J].通信学报,1999(04):72-75.

[5] 梅文华,杨义先.宽间隔的跳频序列族[J].通信学报,1997, 17(05):37-44.

[6] 丁文霞,王浩,卢焕章,等.混沌保密通信系统中平凡密钥现象的探讨[J].通信技术,2007,29(06):29-31.

[7] 刘俊杰，王翔.差分跳频通信系统的特点及性能[J].信息安全与通信保密,2006(09):77-79.

[8] 许娟，胡荣林，金鹰.改进混沌调制技术的抗多径干扰性能研究[J].通信技术，2009，42(02):30-32.

[9] 何海莲,王光义.超混沌序列对DS-UWB多址性能的改善[J].通信技术,2009,42(01):36-38.