改进的实对称阵特征值分解并行化算法
2010-08-06金鹰翰赵景琰王进祥
金鹰翰, 赵 培, 赵景琰, 王进祥
(哈尔滨工业大学, 黑龙江 哈尔滨 150001)
0 引言
波达方向估计技术是阵列信号处理的关键技术之一,其中最具代表性的算法有MUSIC算法[1-2]和ESPRIT算法[3]。这两种算法都需要对接收矢量的协方差矩阵进行特征值分解,且该部分占算法的主要运算量,通过实数化方法可以将协方差矩阵转换为实对称阵,因此采用并行算法实现实对称阵特征值分解能显著缩短算法时间。Jacobi算法是对称阵特征值分解的常用算法,该算法为串行算法,需要时间随矩阵阶数增长迅速增长。David J. Kuck和Ahmed H. Sameh提出了一种基于Jacobi算法的并行算法[3],但由于算法对矩阵元素重复操作,使得算法在实际实现后,效率不是很高。在分析了串行算法和David J. Kuck和Ahmed H. Sameh的并行算法的优缺点后,本文实现了一种更为高效的实对称矩阵特征值分解的并行算法,该算法不增加计算复杂度,经过计算机仿真,效率有很大提高。
1 基于Jacobi算法的实对称阵特征值分解并行算法
在实对称矩阵特征值分解的串行算法中,通常采用Jacobi算法求矩阵的特征值和特征向量。David J. Kuck和Ahmed H. Sameh提出了一种基于Jacobi算法的实对称阵特征值分解并行算法。串行Jacobi算法每次正交旋转变换只消去将两个非对角线元素,而通过如下正交旋转变换可以消去n个非对角线元素(n为矩阵阶数,这里只考虑偶数阶矩阵,奇数阶矩阵多出的一行和一列可以单独处理)。


为了给下一次变换做准备,需要做以下变换:


其中:即将Ak+1的第2行移到最后一行,第2行以后各行依次向前移一行;将Ak+1的第2列移到最后一列,第2列以后各列依次向前移一列。
在实现中,发现此算法效率仍不是很高,主要原因是重复消去矩阵非对角线元素。以8阶矩阵为例,第一次变换消去矩阵上三角元素(由于是对称阵,只列出上三角元素)而第三次变换消去的元素对应于消去原矩阵元素与第一次变换存在大量重复消去元素。
2 改进的实对称阵特征值分解并行化算法
针对David J. Kuck和Ahmed H. Sameh提出的并行算法的缺点,本文提出了一种改进的实对称阵特征值分解并行化算法。保留了原并行算法中的并行正交旋转变换而通过修改φ矩阵,减少重复消去元素的个数,并且只使用一种变换。
φ矩阵应为n阶矩阵,每行每列有且仅有一个元素为1,其余元素均为0,可以用1到n的一个排列表示。φ矩阵第i行第j列元素为1,表示将的第i行移到第j行,第i列移到第j列。为记录经过变换后的矩阵元素与原矩阵元素的位置对应关系,构造矩阵,对所有非对角线的上三角元素进行编号。记录元素,即正交旋转变换消去的元素在原矩阵中的对应位置,然后经过变换A'=φTAφ。重复上述操作n-1次,如果记录的值包含1到n(n - 1 )/2的所有值,则说明经过 n -1次变换,可以将所有非对角线元素无重复无遗漏地消去一遍。
计算φ可以通过生成1到n的所有排列,然后验证符合上述条件的排列。满足条件的排列有多个,如下给出6阶矩阵的一种变换矩阵中值为一的元素,其余元素均为零:

3 硬件结构
图1为根据改进的特征值分解算法实现的模块内部结构。实对称矩阵和特征向量矩阵使用存储器实现,变换 A =φTAφ并不需要对存储器进行读写,只需要控制数据选择器读存储器的地址即可实现。数据选择器和数据分配器由一个状态机控制,负责访问存储器,数据选择器将数据传给运算单元,数据分配器将结果存回存储器。运算单元完成如下运算:

正交旋转变换中的矩阵乘法都可以分解成这种运算。

图1 硬件模块结构
图2为运算单元硬件结构,该结构将该运算过程分为计算θ和完成矩阵乘法两部分,采用CORDIC算法[4]可将正弦、余弦和乘法运算转化为加法和移位运算,便于硬件实现。
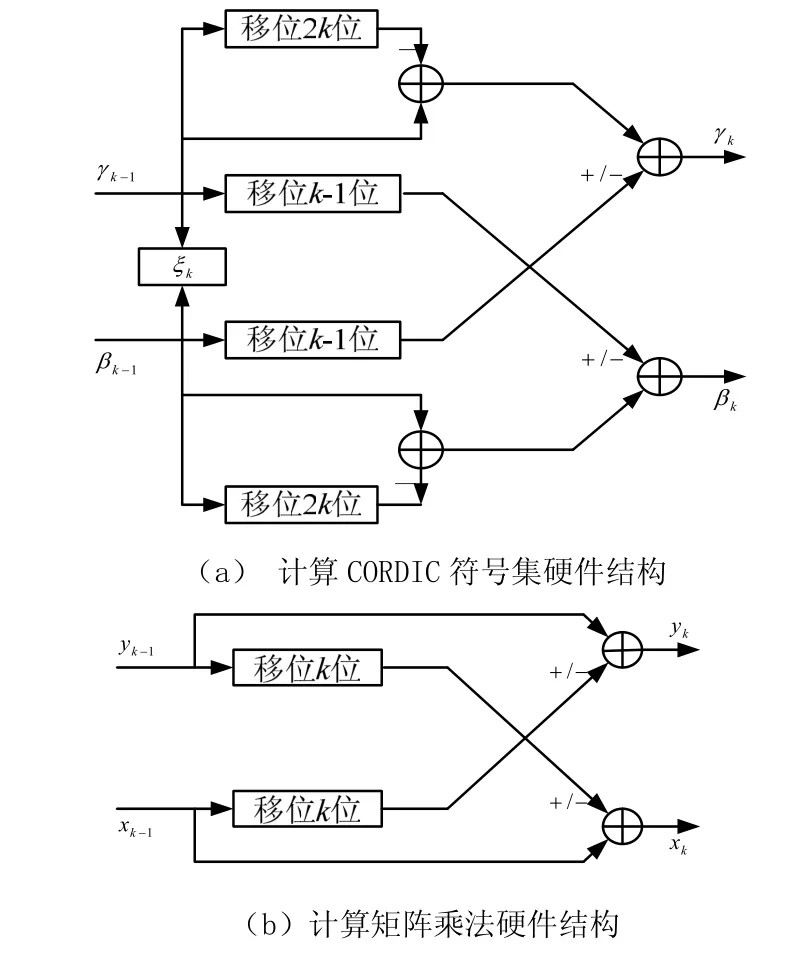
图2 计算单元硬件结构
图2(a)为计算CORDIC符号集的结构,kξ为CORDIC符号集寄存器,控制右边两个加法器进行加运算还是减运算。图2(b)为完成矩阵乘法的结构,同样由kξ控制加法器进行加或减运算。运算单元最多可以并行2/2n 个,可以根据设计要求选择。
下面分析同样根据以上硬件结构,串行 Jacobi算法、David J. Kuck和Ahmed H. Sameh算法和本文改进算法的运算量。假定CORDIC算法的阶数为m,分解n阶矩阵。
串行 Jacobi算法:单次迭代需要(6n+4)m次移位和(6n+4)m次加/减运算。完成一轮迭代(即将所有上三角元素消去一遍)需要n(n-1)(3n+2)m次移位和n(n-1)(3n+2)m次加/减运算。需要4轮迭代可以满足要求,需要4n(n-1)(3n+2)m次移位和4n(n-1)(3n+2)m次加/减运算。
David J. Kuck和Ahmed H. Sameh算法:完成一轮迭代需要n(n-1)次单次迭代,一般需要2轮迭代,所以总共需要2n2(n-1)(3n+2)m次移位和2n2(n-1)(3n+2)m次加/减运算。
改进算法:改进算法需要4论迭代,单次迭代的运算量与David J. Kuck和Ahmed H. Sameh算法相同,总运算量与串行Jacobi算法相同。可见当n>4时,改进算法的运算量要小于David J. Kuck和Ahmed H. Sameh的算法,且n越大,改进效果越明显。
4 计算机仿真
在MUSIC算法仿真中,分别使用David J. Kuck和Ahmed H. Sameh提出的并行算法和本文提出的改进的并行算法进行特征值分解,两者均能得到正确的结果。表1为不同天线阵元数MUSIC算法20次仿真的平均统计数据,天线采用均匀圆阵模型,信号源数均为 3,采用随机正整数序列输入,最大幅值分别为2、4、8,精度为10-4。

表1 仿真统计数据
5 结语
本文在实现波达方向估计MUSIC算法时,针对占主要运算量的实对称阵特征值分解提出了一种改进的并行算法。该算法保留了David J. Kuck和Ahmed H. Sameh提出的并行算法中并行化的思想,同时解决了其重复消去矩阵元素的缺点。由于该算法增加的矩阵变换不需要对存储器进行读写,只需要控制数据选择器读存储器的地址即可实现,因此便于硬件实现,控制较简单,不增加计算量,效率得到了明显提高。由仿真数据可以看出,改进效率随着矩阵阶数增加而提高。
[1] Schmidt R O. Multiple Emitter Location and Signal Parameter Estimation[J].IEEE Transactions on Antennas and Propagation,1986,34(03):276-280.
[2] 张家平,刘青,张洪顺.低信噪比中 MUSIC算法研究[J].通信技术,2009,42(01):87-89.
[3] 龙娟,周围,吴江华.TD-SCDMA中DOA估计的一种ESPRIT算法[J].通信技术,2007,40(09):31-33.
[3] Kuck D J,Lawire D H,Sameh A H.High Speed Computer and Algorithm Organization[M].New York:Academic Press,1977:71-84.
[4] Kim M,Ichige K,Arai H.Design of JACOBI EVD Processor Basedon CORDIC for DOA Estimation with MUSIC Algorithm[C]//The 13th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC 2002).Lisbon,Portugal:IEEE, 2002:120-124.
