基于网络演算的无线蜂窝网建模及其业务匹配研究
2010-08-04倪锐周武旸卫国
倪锐,周武旸,卫国
(中国科学技术大学 无线网络通信实验室,安徽 合肥 230027)
1 引言
随着各种无线接入技术的进步和应用,无线蜂窝网络的空中接口的传输能力日益提高,分组数据逐渐成为主流业务。在此背景下,电信运营商迫切希望部署一些新的业务类型,实现资源利用率和商业收益率最大化的目标。
文献[1]完整分析了确定性网络演算理论,给出了最坏情况下的网络性能下限。文献[2]则将网络演算理论从确定性拓展到随机性,提出了随机性网络演算理论,并分析了其统计复用增益。文献[3]进一步将网络演算理论与有效带宽理论结合在一起,分析了不同调度算法下不同优先级业务流的网络性能,并给出了它们的数学表达式。文献[4,5]则完整阐述了有效带宽的思想,给出了被广泛接受的一般通用的有效带宽表达式。
在新业务部署之前,运营商必须充分考虑现有网络与新业务是否匹配,即 1) 网络能够为新业务提供的服务质量是否达到该业务的最低要求,2) 新业务部署后对网络中已有业务的影响是否能够被接受。针对这一问题,本文利用网络演算[1~3](network calculus)理论和有效带宽[4,5](effective bandwidth)理论为无线蜂窝网络进行建模,并加以分析。
基于网络演算理论,本文构造了一个网络演算系统来为无线蜂窝网络进行数学建模,利用不同的流量模型来对业务进行分类,分别计算它们的有效带宽,并与无线蜂窝网络模型进行匹配。与文献[3]不同,本文是从业务的视角出发,以业务的流量模型影响网络演算理论中的有效包络、以业务的具体时延要求约束网络演算理论中的有效网络服务曲线,而不是简单地计算一个有效带宽后代入网络演算的公式中去。最后,本文提出了一套分析无线蜂窝网络与新业务是否匹配的方法,并重新推导了差异化参数后的网络演算性能表达式,为分段分节点独立配置节点参数提供了理论依据。
2 背景知识
2.1 网络演算理论
网络演算理论是一套基于最小加代数的数学演算系统[1],它以广义递增函数为运算对象,主要使用了最小加代数的卷积算子⊗和反卷积算子∅。
考虑一条流经H个网络节点的数据流,如图1所示,分别记广义递增函数 Ah(t)和Dh(t)(h=1,2,…,H)为第 h个节点的输入流量和输出流量。令前一个节点的输出流量等于后一个节点的输出流量,即Dh-1=Ah。Anet为该条数据流的初始输入源,Dnet为最终的汇聚输出。对于每一个网络节点,必然有 D(t)≤A(t),如图 2所示。记B(t)=A(t)-D(t)为t时刻的节点拥塞,W(t)=inf{d≥0 A(t-d)≤D(t )}为t时刻的节点时延。

图1 一条经过H个节点的数据流
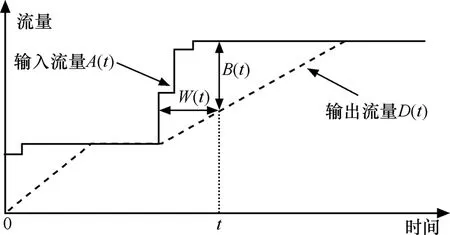
图2 某一个节点的参量示意图
为了对网络中具体节点的性能展开分析,文献[6,7]中定义了到达包络、服务曲线以及网络服务曲线3个概念,分别如下。
定义1 (到达包络)若 ∀t ,τ≥ 0满足

则称A*为输入流量A的到达包络。其中,A*(1)表示在一个时隙内的最大数据流量,相当于该数据流的最大瞬时峰值到达速率。
定义 2 (服务曲线)在网络演算中为保证某数据流的服务质量,网络节点所提供的服务曲线S(t)必须是一个满足式(2)的广义递增函数。
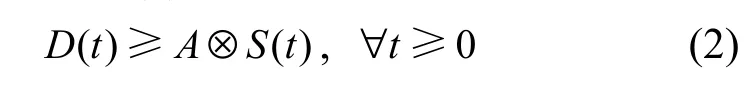
服务曲线是节点提供服务的下限。离开约束包络可表示为A*∅S;拥塞 B的上限可表示为 A*∅S(0);若sup{A*(τ-d)-S(τ)}≤0成立,则可保证时延Wτ≥0的小于等于d。
定义 3 (网络服务曲线)网络对一条数据流总的服务曲线表示为Snet,其满足

由于定义2给出的服务曲线是一条理论下限,在实际分析计算过程中难以使用。所以,在通常情况下剩余服务曲线被广泛使用,它与网络节点的带宽和调度算法密切相关。在基于业务优先级的调度算法中,记优先级为 q的业务的到达包络为 Aq*,则优先级为p的业务的剩余服务曲线可表示为
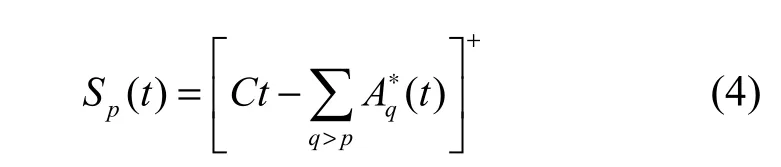
其中,C是网络节点输出链路的信道容量,符号S表示剩余服务曲线,而[x]+=max(0,x)。
文献[3]在综合考虑网络节点的概率随机性因素的前提下,扩展了到达包络、服务曲线和网络服务曲线的概念,分别对应地提出了有效包络、有效服务曲线和有效网络服务曲线的概念,将网络演算的应用范围从确定性场景扩展到了随机性场景。
定义4 (有效包络)若 ∀t ,τ≥ 0满足

则称Gε为输入流量A的有效包络。当ε=0时,Gε即为定义1中的A*。
定义5 (有效服务曲线)若∀t≥0满足

则称Sε为输入流量A的有效服务曲线。当ε=0时,Sε退化为定义2中的S。
定义6 (有效网络服务曲线)若H个网络节点的服务曲线 Sh,εs(h=1,2,…,H),都满足式(6),这里εs表示服务曲线的概率,则有效网络服务曲线Snet,ε可表示为

其中,ε表示为

与确定性理论相比,随机性网络演算理论最重要的改进在于定义了 2个基于概率的统计量Gε和Sε。当ε=0时, Snet,ε退化为定义3中的 Snet。
需要特别指出的是:为了在统计概率的前提下有效简化式(5),定义时间尺度T,满足

这里,T实质上约束了式(5)中的最小加卷积的作用范围。
2.2 有效带宽理论
有效带宽理论是一种描述突发性业务流量的统计复用性能的方法,文献[4]给出了一个被普遍接受的有效带宽表达式:
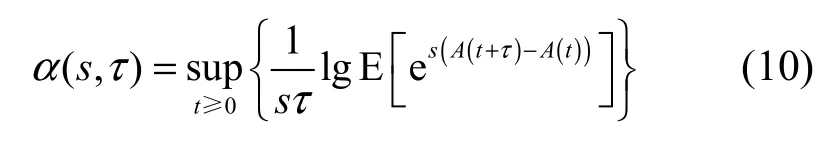
其中,符号τ称为时间参数,用以表示时间的间隔长度;符号s称为空间参数,用以描述业务流的到达分布特征。当s→0时,有效带宽主要由该业务流的均值速率决定,当s→∞时,有效带宽主要由该业务流的峰值速率决定。
通过建立有效带宽和有效包络之间的联系[3,5],可以用来分析突发性业务流的各种网络性能。
定理1 对于一条有效带宽为α(s,)τ的业务流A,它的有效包络可表示为

对于一条有效包络Gε,已知的业务流 A,它的有效带宽可以表示为

基于网络演算理论,本文将无线蜂窝网络抽象为一个类似于图1所示的多节点模型,并利用有效带宽理论,分别计算无线蜂窝网络中所运行的不同业务流量的有效带宽。在此基础上,本文将进一步展开对无线蜂窝网络和业务是否匹配的研究。
3 无线蜂窝网建模
本文将无线蜂窝网建模为一个网络演算系统,如图3所示。首先,该模型将有线核心网络视作一个节点(对应于节点3),其通信能力远远高于无线接入网。其次,该模型将用户终端与业务信源/宿加以区分,认为用户终端也是模型中的节点,节点1的输出流量和节点5的输入流量都受制于无线链路。然后,将 5个节点系统之间的4条链路分别抽象为4个独立不相关的信道容量。最后,该模型假设业务信源至终端1和终端2至业务信宿的CPU芯片处理能力足够强大,相比于网络中的传输时延,在后继分析中将忽略CPU的处理时延。
在网络演算系统模型中的剩余服务曲线Sh(h=1,2,…,H ),由网络通信链路的信道容量和网络节点的调度策略共同决定。特别的,本文假设S5足够大到对业务性能不会产生瓶颈约束。网络演算理论的数学符号与实际网络的物理概念的映射关系如表1所示。

图3 无线蜂窝网的5个节点网络演算系统建模
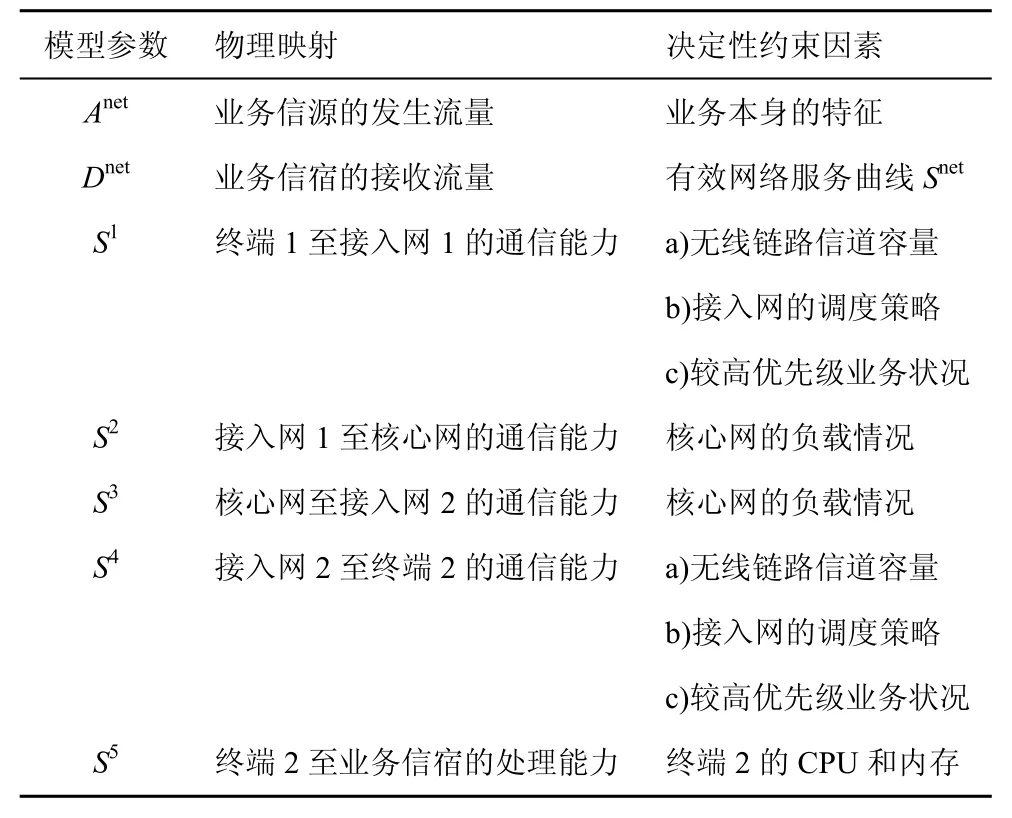
表1 模型参数的物理映射关系
给定一个无线蜂窝网,由网络所决定的Sh(h=1,2,…,H ),并不一定能够为流量为Anet的业务提供其所要求的网络服务曲线 Snet,网络和业务之间存在一个是否匹配的问题。
在如图3所示的无线蜂窝网的网络演算系统模型中,H=5,记 5个节点的剩余服务曲线分别为Sh,εh(h=1,2,…,H);而每个节点的时间尺度分别记为Th(h=1,2,…,H);则式(7)的计算结果为

其中

如果εh对于不同的节点都相等,记为εs,则式(14)将退化为式(8)。
4 业务与网络匹配分析
本文所讨论的无线蜂窝网中的业务重点关注于通信技术视角下的业务流量特征,忽略业务的具体内容和所含信息量。此外,由于网络演算理论本身的特征决定了它仅适合分析点到点的单条流或者较为简单的并发场景,不适合分析多输入多输出很复杂的拓扑结构。因此,本文后面的分析集中于点到点的业务类型,其结论尚无法简单推广到多点到多点的场景下。
4.1 基于流量模型的蜂窝网业务分类
本文将各种业务根据其流量模型的不同归纳为3种业务类型,分别是受约束流、无记忆开关流和分形布朗运动流,如表2所示。
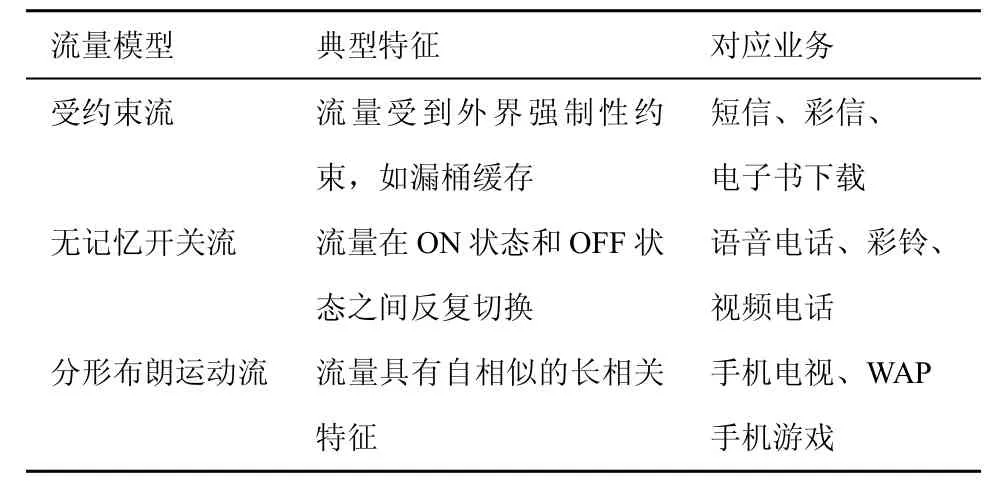
表2 流量模型及其业务映射关系
对于给定到达包络A*的受约束流,其峰值速率R和均值速率分别定义为 R=A*(1)和=limt→∞(A*(t)/t )。根据文献[5]的结论。其有效带宽满足

根据定理1,进而可得受约束流的有效包络满足
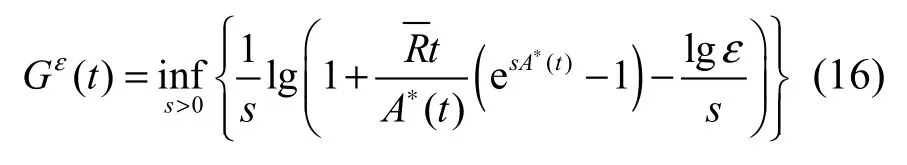
对于无记忆开关流,在ON状态业务以恒定速率 R=A*(1)产生数据流,在OFF状态则没有数据产生,其均值速率仍定义为=limt→∞(A*(t)/t )。其有效带宽满足

无记忆开关流的有效包络满足

对于分形布朗运动流[8],其流量具备显著的自相似特征,输入流量可表示为 A(t)=ρt+βZt。其中,Zt符合自相似参数为H的分形布朗运动,ρ>0为流量的均值,而β2则是A(1)的方差。其有效带宽满足

分形布朗运动流的有效包络满足
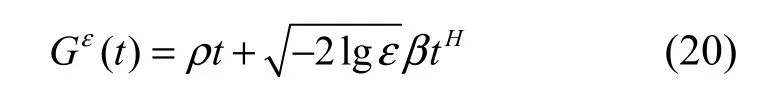
4.2 业务与网络匹配的分析方法
业务与网络相比,后者较为固定且能在一段较长的时间内保持稳定。对于一个给定的通信网络(如无线蜂窝网),从统计的角度看,其链路容量和调度策略大体是不变的。而网络中运行的业务类型及其优先级配置,在大量统计的情况下也是基本稳定的。而业务的具体类型多种多样,其服务质量要求更是各不相同。因此,在业务与网络的匹配过程中,基本思路是将网络视作一个准静态的黑箱,而将具体的业务类型作为动态变化的输入匹配量。
根据对时延的敏感性,业务类型可以分为实时性业务和非实时性业务。具体到无线蜂窝网络中的业务,短信、彩信、电子书下载等业务往往对时延具有较大的容忍性,业务服务质量一般都可以得到保证。但是,视频电话、手机电视等业务对时延很敏感,它们的业务服务质量能否得到网络的有效支持往往是未知的。所以,本文所提出的业务与网络匹配的分析方法着重分析的是那些对时延敏感的实时性业务。如表2所示,无线蜂窝网络中的实时性业务的流量模型可以采用无记忆开关流和分形布朗运动流。
虽然,实时性业务的服务质量往往由速率、时延、抖动等多个技术参量来描述。但是,在本文所提的业务与网络的匹配过程中仅仅考虑时延因素,是否匹配的判决标准就是网络传输时延是否小于业务可容忍的最大时延。
基于网络演算和有效带宽理论的业务与网络匹配流程如图4所示。

图4 业务与网络的匹配流程
从业务类型(如短信、彩信、手机电视)出发,不同的业务决定了它可容忍的最大时延dmax; 同时根据表2,将具体的业务类型映射为不同的流量模型。根据式(15)、式(17)、式(19),可以计算该业务的有效带宽α(s,t)。进一步,根据式(16)、式(18)、式(20),由有效带宽计算概率为εg的有效包络Gεg(t)。至此,可以确定网络输入流量Anet(t)。
从网络(如图3所示的无线蜂窝网)出发,可以直接确定:1)各条链路(包括无线和有线)的链路容量Ch(h=1,2,…,H);2)网络节点的调度策略,在无线蜂窝网中,最常见的最基本的调度策略是固定优先级(static priorities)的先进先出(FIFO)的策略。从网络出发,可以间接确定:比待匹配的业务类型p具有更高优先级的所有业务的统计流量之和进一步,根据式(4)计算得到业务流沿途各个节点的剩余服务曲线 Sh,εh(h=1,2,…,H)。这里的εh表示第h个网络节点可以以概率(1-εh)确保为业务提供 Sh,εh的剩余服务曲线。然后,根据式(7)计算有效网络服务曲线 Snet,ε。
在分别求得了业务的有效包络和网络的有效服务曲线之后,可以根据下式计算网络传输该业务的实际时延dnet:
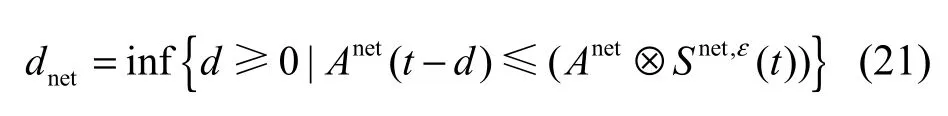
最后将服务质量所能容忍的最大时延dmax与网络的实际时延 dnet进行比较,若 dmax>dnet,则不匹配;否则,匹配。
如图4给出的业务与网络的匹配流程所得到的结论是以时延作为服务质量的评价标准,回答了业务匹配的第1个问题:网络能够为新业务提供的服务质量是否达到该业务的最低要求。
对于业务匹配的第2个问题:新业务部署后对网络中已有业务的影响是否能够被接受。其解决思路如下:1)对优先级高于新业务的已有业务,性能没有影响;2)对优先级低于或等于新业务的已有业务,性能有影响。分析具体影响大小的方法是采用图4流程分析完毕新业务之后,利用式(4)计算得到优先级较低的已有业务的剩余服务曲线,然后按图4方法重新分析在新的可用剩余服务曲线条件下,已有业务的时延性能是否匹配。
在面对如下具体问题时,将超出通信技术的讨论范畴,由电信运营商权衡利弊后取舍决定:1)新业务与当前网络不匹配,新业务性能无法达到最低要求,是否重新设计该新业务?2)新业务与当前网络不匹配,新业务性能无法达到最低要求,是否对网络进行扩容?3)新业务与已有业务发生冲突时,新业务与已有业务之间如何取舍?
5 仿真示例
考虑一个采用WCDMA技术的3G无线蜂窝网络。在查阅现有通信工程技术标准中所提性能参数的基础上,本文略作简化和近似后确定各段通信链路的带宽及时间尺度如表3所示。已有业务类型包括语音电话和短信,而电信运营商准备部署一种新的手机电视业务。设定业务优先级从高到低分别为语音电话、手机电视、短信,三者业务可容忍的最大时延分别为50ms、100ms、180s。

表3 无线蜂窝网的仿真参数配置
如图5所示,以节点1与节点5之间的手机电视业务流为目标流。此外,考虑接入网和核心网部分的2条业务流,分别记为竞争流1和竞争流2。假设在手机电视业务部署之前,无线网络中的竞争流1的输入流量A(t)仅由语音电话和短信流组成,以 概 率 参 数 ε=10-3满 足而有线网络中的竞争流2的输入流量的业务类型种类繁多,令所有优先级高于手机电视的业务流量之和以概参数率 ε=10-6满足

图5 仿真场景示意图
因为有线核心网的可用带宽远远大于无线接入网,所以忽略核心网对服务质量形成制约的情况。根据式(4),对于准备部署的手机电视业务,其各个网络节点的剩余服务曲线及其概率参数如表4所示。进一步,根据式(13)和式(14)计算可得Snet,ε=5.25t ,其中 ε=1.025×10-2。物理含义为无线蜂窝网以1-ε的概率为所有的手机电视用户一共提供5.25Mbit/s的传输速率。

表4 无线蜂窝网的仿真参数配置
假设手机电视业务的流量模型为分形布朗运动流,并且所有同类业务用户的参数均相同,具体设为 ρ=128kbit/s , β=100kbit/s , H=0.78。图6反映了当一对无线接入基站之间的手机电视用户数量N从1变化到35时,平均每用户所需的传输速率和所有用户所需的总传输速率的变化趋势。
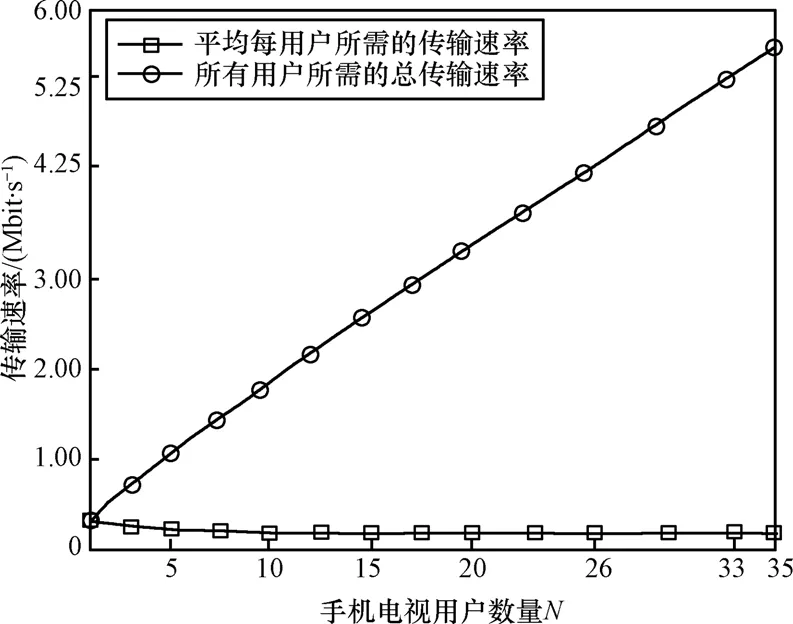
图6 关于手机电视业务的数值仿真
当一对无线接入基站之间手机电视用户 N=1时, Gε=0.31Mbit/s, ε=1.025×10-2。即系统只需要为该业务流提供310kbit/s的传输速率就能以99%的概率确保该条业务流不会超时。随着同类业务用户数量 N的逐渐增加,将产生统计复用增益。当N=35时,系统平均为每条流提供160kbit/s的传输速率就能以99%的概率确保上述流不会超时。从图6可见,当N≤33时,网络能够为所有手机电视业务流提供相应的服务质量保证,即满足业务与网络是否匹配的第一个问题。
考虑到网络中已有的业务,不论是否部署手机电视业务,均不会影响优先级较高的语音电话业务。但是,对于优先级较低的短信业务,从图 6可见,当26 < N≤33时,手机电视业务的服务质量可以保证,但是短信业务的服务质量将因为没有足够的可用带宽而得不到保证。当N≤26时,短信业务不会受到影响,即满足业务与网络是否匹配的第2个问题。
综上所述,在本仿真示例中,在3G无线蜂窝网中部署手机电视新业务,为了确保业务与网络的匹配,要求平均每个无线接入基站的该类业务流数量不超过26条。此时,网络以99%的概率保证手机电视业务的服务质量,并且不会影响其他已有业务的服务质量。
6 结束语
在一个给定的网络中部署新业务类型,需要预先考察该网络与新业务是否匹配。本文将无线蜂窝网建模为一个网络演算系统,并将各种典型的蜂窝业务类型按照其流量模型加以分类,给出了一套分析业务与网络是否匹配问题的新方法。该方法基于数学推导来分析业务在网络中的性能,可以为未来通信系统中新业务的开发和部署提供参考。
本文提出的网络演算系统将随机性网络演算理论与实际的无线蜂窝网相结合,在数学符号与实际系统的物理量之间建立映射关系。本文改变了所有网络节点的参量和概率都相等的假设,重新推导了有效网络服务曲线和网络时延的概率表达式,为后继的分段分节点地差异化分析提供了理论依据,为不同节点独立配置参数提供了方便。
[1] CRUZ R L.A calculus for network delay,parts I,II[J].IEEE Transaction on Information Theory,1991,37(1): 114-141.
[2] BURCHARD A,LIEBEHERR J,PATEK S D.A min-plus calculus for end-to-end statistical service guarantees[J].IEEE Transaction on Information Theory,2006,52(9): 4105-4114.
[3] LI C Z,BURCHARD A,LIEBEHERR J.A network calculus with effective bandwidth[J].IEEE/ACM Transaction on Networking,2007,15(6): 1442-1453.
[4] KELLY F.Notes on effective bandwidths[A].Stochastic Networks:Theory and Applications[C].New York: Oxford Univ Press,1996.
[5] CHANG C S.Performance Guarantees in Communication Networks[M].New York: Spring-Verlog,2000.
[6] 张信明,陈国良,顾军.基于网络演算计算保证服务端到端延迟上界[J].软件学报,2001,12(6): 889-893.ZHANG X M,CHEN G L,GU J.On the computation of end-to-end delay bound in guaranteed service by network calculus[J].Journal of Software,2001,12(6):889-893.
[7] 李庆华,陈志刚,张连明等.基于网络演算的无线自组网QoS性能确定上界研究[J].通信学报,2008,29(6): 32-39.LI Q H,CHEN Z G,ZHANG L M,et al.Deterministic upper bounds onQoS performance about wireless ad hoc network based on network calculus[J].Journal on Communications,2008,29(6): 32-39.
[8] NORRIS I.On the use of fractional Brownian motion in the theory of connectionless networks[J].IEEE Journal on Selected Areas in Communications,1995,13(6): 953-962.
