八七型铁路应急抢修钢梁的自振特性分析

韩金秀,郭薇薇,夏 禾,纪尊众

(北京交通大学土木建筑工程学院,北京 100044)

1 概述

八七型铁路应急抢修钢桁梁是根据总参和国家交战办批准的战术技术要求研制的铁路大跨度军用桥梁。1987年鉴定定型后,获国家科技进步二等奖,并已批量生产,装备铁路局、工程局,成为我国交通战备主要器材之一。它应用于大跨度桥梁战时及平时抢修,是一种可以快速装拆反复使用的临时性桥梁,对于战时和自然灾害时期保障交通运输的畅通无阻具有重要的意义。

八七型梁基本设计跨度 40～80m,最大设计跨度96m。跨度序列,既符合国家标准规定的标准跨度,也可按 1m变换跨长,以适应非标准跨度需要。部件种类少,单元质量轻,结构简单,组合方便,拼架速度快。八七型梁可以拼组成上承式、穿式和半穿式梁,上承式梁又可分为低鱼腹式、鱼腹式和齐头式。上承式梁桁高 4.34m,梁宽 2.90m,跨度范围 40～64m,其中跨度40～56m的行车限制速度为 40 km/h,跨度 57～64m的行车限制速度为 30 km/h;半穿式梁桁高 4.34m,梁宽 5.388m,跨度范围 40～56m,行车限制速度为 30 km/h;穿式梁桁高 8.68m,梁宽 5.388m,跨度范围 64～96m,其中跨度 64～80m的行车限制速度为 40km/h,跨度 81～96m,的行车限制速度为 15 km/h。

上承式梁拼组架设最方便,质量最轻,抢修速度最快,综合战术技术性能最好,在 64m跨度以下应属首选[1]。材料主要为 15MnvNq和 16Mnq。基本部件共36种,其中弦杆主要有 3种,工字形截面,杆件长 7.98 m。连接系部件主要有 3种:直撑,L形截面,杆件长2.488m;长斜撑,槽形截面,杆件长 2.97m;小横撑,L形截面,长 2.020m。主桁腹杆 8种,主要为两槽钢和钢板拼成的组合截面。桥面系部件主要有两种:短横梁,工字形截面,长 2.488m;纵梁,工字形截面,长4m[2]。

上承式梁,桁高 4.34m,梁宽 2.90m,相对较小,刚度比较低,行车限速为 30～40 km/h。为了更好适应未来战争后勤保障和平时突发事件中提速后铁路桥梁应急抢修的需要,对定型设计(1987)做必要变更,检算其动力特性。桥梁的自振特性在很大程度上反映桥梁刚度大小也反映出桥梁的动力特性,是评价桥梁动力特性的重要依据,也是对桥梁动力特性进行准确分析和计算的基础,因此本文根据八七梁特点,用大型有限元软件 ANSYS建立 64m上承低鱼腹式模型,计算并分析其自振特性,为动力计算及提速设计提供依据。并分别以普通有限元方法和子结构方法建立模型,探讨子结构方法在八七梁自振分析中的应用。

2 有限元模型

2.1 八七梁特点

八七型梁为铁路应急抢修钢桁梁,由可拼装的基本杆件通过节点板用高强螺栓连接。原定型设计中,设上平纵联,不设下平纵联,下弦杆件只在端头设 8根小横撑做横向连接。各杆件间的连接较弱,梁的横向刚度较低。

2.2 建模过程

采用 BEAM 44单元建立有限元模型。在梁单元中输入各杆件截面形式,其中主桁腹杆为组合截面,采用自定义截面。通过定义不同的方向点,确定各杆件截面的不同方向。为更好地模拟各杆件间的位置关系,将梁节点偏移到横截面原点处[3～5]。

在各杆件栓结处,假设节点为刚结,无螺栓连接但杆相交处假设其不直接传力,建模时交点不断开。纵梁杆件与联结系相交处无螺栓连接,在建模过程中联结系的斜撑与横撑只在端部与弦杆相交,交点为刚结;联结系与纵梁相交处不断开。其余杆件交点视为刚结 ,见图1～图3。

考虑到节点板、螺栓和桥面铺装的质量,以换算密度形式均匀加到各单元中。换算密度为 10.35 t/m3。

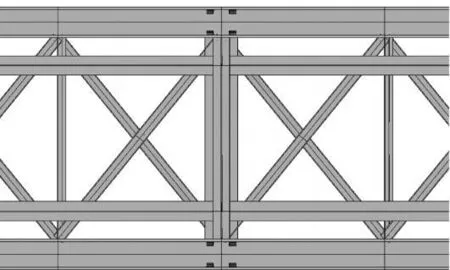
图1 局部模型

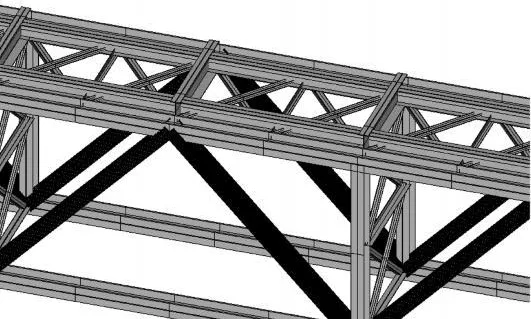
图2 局部模型

图3 全桥模型

2.3 计算结果

应用 Block Lanczos方法对模型进行模态分析,计算前 10阶自振频率和振型,结果见表1。

为保证桥梁具有足够的横向刚度,我国《铁路桥梁检定规范》规定,低合金钢桁梁的实测横向最低自振频率通常值为 f≥90/L[5]。八七梁计算所得 1阶横向自振频率 1.23Hz,小于规范通常值1.41Hz,比普通低合金钢桁梁桥刚度低,其刚度问题需要进行专门的研究。

表1 自振特性计算结果

2.4 模态分析比较

通常桥梁的振动可分为横向振动、竖向振动、扭转振动、纵向振动以及他们的组合振动。本文列出了 64m低鱼腹式八七梁的前 10阶模态,包括横向振动和扭转的组合振动、竖向振动,下弦端部杆件的竖向振动。

在前 10阶振型中,出现两阶竖向振动,分别出现在第 2阶和第 10阶,频率分别为 2.77、8.45Hz。在竖向二阶反对称中端部下弦杆件振幅较大,见图4。

图4 竖向振动振型

计算结果显示,64m低鱼腹式八七梁在横向振动的同时伴有扭转振动,并无单一的横向振动或扭转振动出现。横向振型前 10阶振型中出现 4次,且出现较早。第 1阶为横向和扭转的组合振型,频率为 1.23 Hz,其余 3次在 3、4、5阶连续出现,频率为 3.29、3.69、6.27Hz。说明该梁的横向刚度低,尤其下弦杆件间横向连接较弱,需要提高横向刚度,以满足列车以较高速度通过。图5给出了各阶横向和扭转组合振动的振型图。

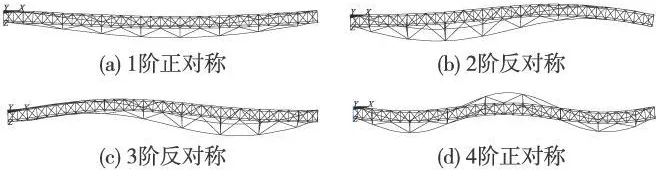
图5 横向与扭转组合振动振型

3 子结构方法

子结构就是一组单元通过保留部分自由度的静力凝聚而生成一个新单元,这个单一的新单元又称为超单元。应用子结构方法的主要目的是为了节省机时,提高分析效率,在有限的计算机设备资源基础上求解超大规模问题[6～7]。

在 ANSYS中,一个典型的子结构分析过程分为 3个步骤:生成部分、使用部分和扩展部分。

(1)生成部分:将普通的有限元凝聚为一个超单元。凝聚是通过定义一组主自由度来实现,主自由度由于定义超单元与模型中其他单元的边界,提取模型的动力学特性。

(2)使用部分:将超单元与模型整体相连进行分析。整个模型可以是一个超单元,多个超单元,或由超单元与非超单元相连。使用部分的计算结果是超单元的凝聚解(主自由度解)和非超单元的完全解。

(3)扩展部分:由超单元的凝聚扩展到整个超单元所有自由度上的完整解。如果有多个超单元,每个超单元都需要有单独的扩展计算[8～11]。

在八七梁结构中有很多重复的部分,因此将重复部分作为子结构生成超单元,复制生成其他部分,还可以快速组合成不同跨度,节省大量机时。

以 64m上承式八七梁为例,中间 3个节间几何形状重复相应杆件截面完全相同,可将这部分采用子结构建模避免重复建模的复杂过程。

首先建立 1个节间的有限元模型,在生成部分读入已建有限元模型,定义左、右界面上的节点为主自由度生成超单元(图6)。在使用部分,建立两端非子结构部分的有限元模型,读入超单元,耦合超单元间连接节点及超单元与非超单元连接节点,生成整个模型(图7),施加约束求解。在扩展部分扩展超单元的凝聚解得到超单元内所有自由度的完全解。有限元法与子结构法结果对比见表2。

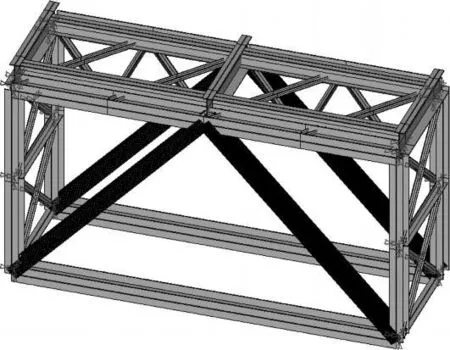
图6 超单元

图7 整体模型

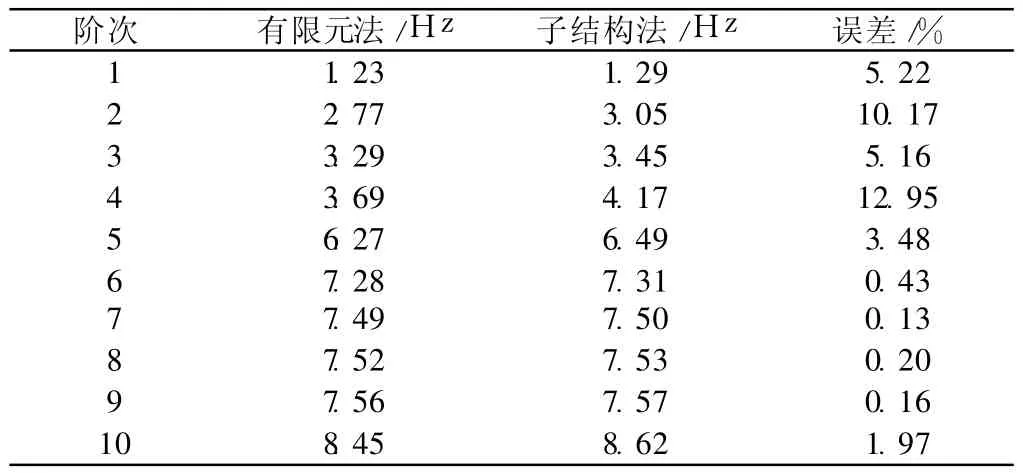
表2 子结构法与有限元法对比

由表2可见,应用子结构方法计算结果与有限元法计算结果基本接近,误差在合理范围内,部分误差较大。这是因为,采用子结构方法生成超单元,是将子结构部分的质量和刚度矩阵静力凝聚到主自由度的质量和刚度矩阵上,必然不能真实地反映子结构的部分的动态特性。

4 结论

(1)八七梁 1阶竖向振动频率的计算结果和试验结果对比误差约为 4%,说明所建立的有限元模型比较合理,能较好地反映真实情况。

(2)计算所得的八七梁 1阶横向自振频率 1.23 Hz,小于《铁路桥梁检定规范》的通常值 1.41Hz,说明八七梁比普通低合金钢桁梁桥横向刚度低,其刚度问题需要进行专门研究。

(3)八七梁振型前几阶多为横向和扭转的组合,无单一的横向振动和扭转振动,且在第 1阶就出现,频率仅为 1.27Hz;在竖向二阶反对称振型中端部下弦杆件振幅较大,且后几阶多为端部下弦杆件竖向振动。以上结果说明此梁横向刚度低,尤其下弦杆件间横向连接较弱。如需提高列车通过速度,需要对结构进行加强以提高其刚度,尤其是横向刚度。

(4)应用子结构方法建立八七梁模型进行动力分析,结果误差在合理范围内,部分误差较大。采用子结构方法将子结构部分的质量和刚度矩阵静力凝聚到主自由度的质量和刚度矩阵上,不能真实反应结构的部分动态特性。

[1] 张增勤.铁路桥梁抢修技术研究[J].铁道建筑技术,2008(增).

[2] 宋德文,黄耀怡.八七型铁路应急抢修钢梁手册[M].北京:中国铁道建筑总公司,1991.

[3] 王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2007:182-193.

[4] 张亚齐,刘嘉武,陈士通.铁路抢修钢梁仿真分析探讨[J].国防交通工程与技术,2005(4):24-26.

[5] 铁道部运输局.铁路桥梁检定规范[M].北京:中国铁道出版社,2004.

[6] 尚晓江,邱 峰,赵海峰.ANSYS结构有限元高级分析方法与范例应用[M].北京:中国水利水电出版社,2008:349-366.

[7] 何 斌,孙千伟,唐伟平.子结构在大型结构有限元分析中的应用[J].山西建筑,2007(4):119-120.

[8] Erdogan Madenci,librahim Guven.The finite element Method and applications in engineering using Ansys[M].

[9] C.S.Krishnamoorthy.Finite Element Analysis[M].

[10] 周海亭,陈莲.子结构方法在 ANSYS软件中的应用[J].噪声与振动控制,2001(8):15-18.

[11] 马少坤,于 淼,崔皓东.子结构的基本原理和 ANSYS软件的基本方法[J].广西大学学报,2004(6):150-153.