两相流喷射器流动模型研究

陈 亮 刘敬辉 陈江平 陈芝久

(上海交通大学制冷与低温工程研究所 上海 200240)

喷射器是由Charles Partson于1901年发明的，1910年Maurice Leblanc第一次将喷射器用于蒸汽喷射式制冷系统[1]。喷射器作为膨胀装置用于亚临界制冷循环是由Kemper和Harper等人在1966年发明的[2]。近年来，随着世界能源局势的日趋紧张，以及制冷空调系统在能源消耗中占的比重日益增大，制冷系统的节能问题又再次引起人们的重视。Harrell[3]用R134a作为工质对两相流喷射器进行了实验测试，结果显示COP比传统制冷循环提高3.9%到7.6%。日本DENSO公司[4]在冷藏车上用喷射器替代膨胀阀后，COP提高了50%。喷射制冷系统性能提高的关键在于喷射器的设计，而合理设计的前提就是弄清喷射器内部流动的机理。

压缩/喷射制冷循环各部件连接方式及喷射器的结构分别如图1(a)、图1(b)所示。与传统蒸汽压缩制冷循环相比，它的最大不同是从冷凝器来的高温高压液态制冷剂直接进入喷射器的喷嘴，在喷嘴内加速降压将压力势能转变为动能，从喷嘴喷出的低压高速制冷剂引射从蒸发器来的低压低温气态制冷剂，并在混合室混合均匀后，再在扩压室内减速升压使动能转变为压力势能，从而使从蒸发器来的制冷剂压力升高，在气液分离器内进行气液分离后气态制冷剂进入压缩机，吸气压力高于蒸发压力，液态制冷剂进入蒸发器，更有效地利用了蒸发器换热面积，从而使制冷系统的效率得以提高。

在两相流喷射器内，主要的研究对象有两个，一是两相流喷嘴内主射流的发展过程；另一个是喷射器内部混合及扩压段的主射流与引射流的混合及扩压过程，这是最复杂并且对喷射器性能影响最大的过程。这里主要针对后者进行研究，对于喷嘴只给出喷嘴出口的几种可能流动状态，作为喷射器研究中的主射流初始条件。对于喷射器的研究，比较关键的问题是喷射器内部的射流混合过程，目前检索到的关于压缩/喷射制冷循环的文献中还未见到从微观混合机理的角度来研究射流混合过程的，而都是将混合过程看成黑箱，应用质量、动量、能量守恒定律研究混合室进出口的状态变化[5-7]，对主射流与引射流混合室内流动的实际细节并不进行研究，而实际上喷射器混合室中的流动分为两个阶段，即初始混合段和速度均匀段，这两段的细分研究对于喷射器的结构优化设计和性能分析都非常重要。针对喷射器内部射流的流动过程，分段对压力调整、射流混合、均匀和扩压过程进行建模，计算得到引射比和出口背压，并进行了实验测试对模型的有效性进行了验证。

图1 喷射制冷循环及喷射器结构Fig.1 The ejector cycle and structure

1 喷射器内部流动过程分析

从喷嘴出来的超音速主射流和从吸气室来的引射流在喷射器内的流动混合过程如图2所示，可分为三个阶段：1)主射流的压力调整过程。由于混合压力一般与喷嘴出口压力不同，从喷嘴出来的超音速流在喷嘴出口会发生激波(混合压力高于喷嘴出口压力)或膨胀波(混合压力低于喷嘴出口压力)，在此期间主射流与引射流的混合作用不明显，而是形成了一个主射流的虚拟管道，经过压力调整后的主射流压力与混合压力相同；2)主射流与引射流的混合过程。主射流高速流入混合室，将引射流卷吸到主射流中，进行动量和能量的传递，同时进行着液滴浓度的扩散，随着射流的发展，主射流和引射流的混合流体边界层厚度逐渐增大，当边界层发展到喷射器混合室的壁面时，由于壁面的限制，混合过程结束；3)混合完毕后的速度均匀过程。由于主射流和引射流的速度不同，混合流体的中心和周围存在速度差异，混合后的流体继续进行着动量传递，直至混合流体的速度分布均匀。速度均匀后的混合流体继续进入扩压室进行压力回升。

图2 喷射器混合过程示意图Fig.2 The mixing process in ejector

2 喷射器内射流流动模型

为了使问题简化，这里忽略某些次要因素，对喷射器混合过程作如下假设：

1) 混合为等压混合过程，即引射过程结束前混合压力不变，混合压力由喷嘴出口状态、引射流入口状态和喷射器背压共同决定。混合过程不存在汽液相的转变，即液滴的总含量为一定值，液滴的分布随混合过程的发展而变化；

2) 混合的起始点由喷嘴出口压力与混合压力决定。射流的起始点可能位于膨胀波或斜激波后的等效截面的位置，也可能位于喷嘴出口处；

3) 喷嘴出口射流为可压缩流的伴随湍流射流，引射流为饱和气相或两相，主射流和引射流的质量浓度与干度等效；

4) 从混合室出来的流体是速度分布均匀的均相流体；

5) 不考虑喷射器内壁面的摩擦损失。

2.1 喷嘴出口主射流的压力调整过程

当气液两相流体从喷嘴出口流出，主射流与引射流的混合压力(即喷嘴背压)一般不等于流体在喷嘴内正常膨胀时的出口压力，流体势必在喷嘴出口处附近产生膨胀波或激波[8]，喷嘴出口主射流的状态对射流的混合会产生直接的影响。这里重点关注喷射器内射流的混合及扩压过程，因此对喷嘴内部复杂的两相流动过程不加以讨论，仅对出口状态进行研究。这里将两相流体在喷嘴出口的区域按均相流处理，对各种可能的出口射流情况分别进行建模，以此作为喷射器内部流动计算的初始条件。

2.1.1 喷嘴出口膨胀波

当混合压力低于喷嘴正常膨胀时出口处压力时，从喷嘴出来的超音速流为了达到与背压相同，则在喷嘴出口势必发生一道膨胀波，压力降低，速度增大并发生向外偏转，如图3所示。

图3 喷嘴出口膨胀波示意图Fig.3 The expansion wave at the nozzle exit

根据膨胀波前后的状态变化列出质量、动量、能量守恒方程：

2.1.2 喷嘴出口斜激波

当喷嘴背压稍高于正常膨胀时的出口压力时，流体在流出喷嘴时，会发生一道斜激波，压力升高，速度减小并发生向内偏转，如图4所示。

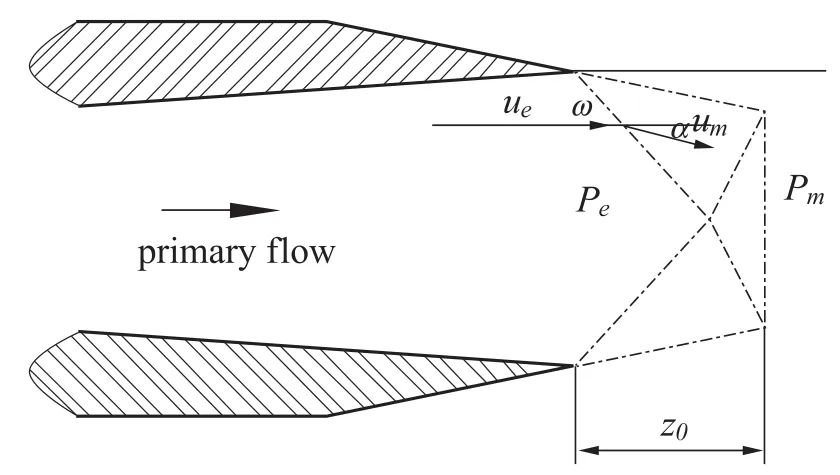
图4 喷嘴出口斜激波示意图Fig.4 The oblique shock wave at the nozzle exit

由质量、动量、能量守恒定律可得[9]：

2.1.3 喷嘴渐扩段内的正激波

当喷嘴背压高于正常膨胀时的出口压力时，在喷嘴渐扩段会发生正激波，如图5所示。

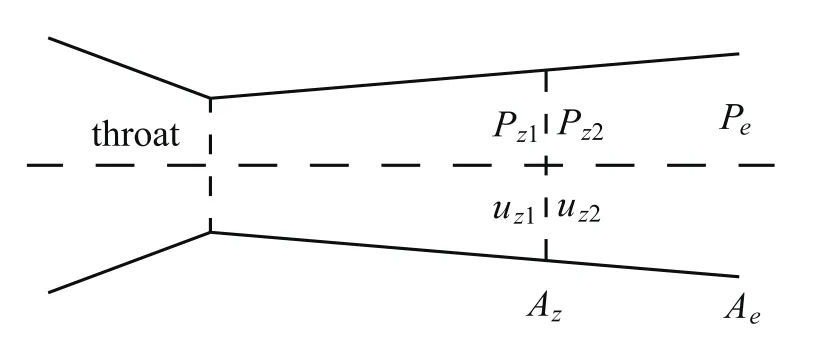
图5 在喷嘴渐扩段内部的正激波示意图Fig.5 The normal shock wave in the divergent section

由正激波理论[8]可得：

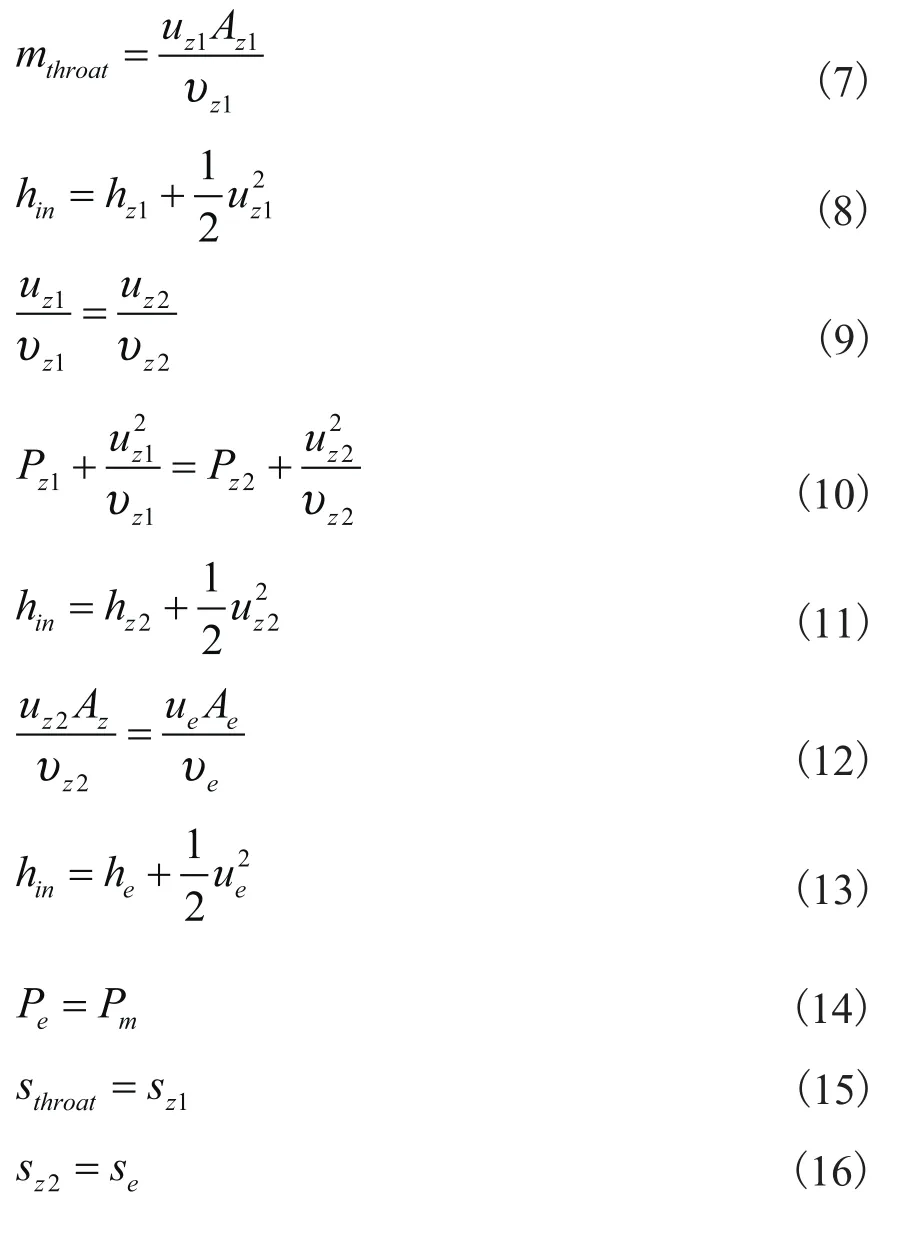
2.2 射流混合过程

从喷嘴喷出的高速流体进入速度相对较低的周围流体中，在交界面处形成速度间断，间断面上会出现涡旋，这些涡旋区域的微团间发生动量、质量交换，并形成射流边界层。而从喷嘴刚喷出的流体由于未与周围流体进行动量交换，流速保持不变，形成一个速度较大的射流核心区。随着射流的发展，射流核心区逐渐萎缩，直至消失，出口射流与周围流体间逐渐发生动量交换，不断把周围流体卷吸入射流边界层，使混合区的厚度逐渐增大。如图6所示，在射流核心消失前的射流区域称为射流初始段，射流核心消失后的区域称为射流主段。根据湍流伴随射流理论[10]，对于轴对称射流，可采用积分的方法对射流参数进行求解。由主射流和引射流混合前后的动量差守恒可得：

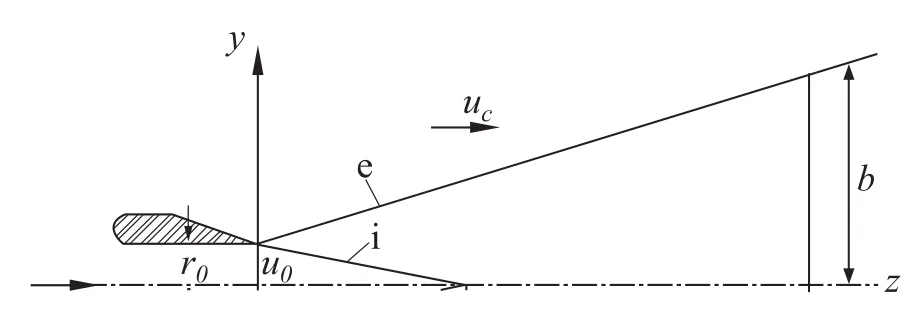
图6 射流混合过程轴对称示意图Fig.6 The mixing process of jet fl ow

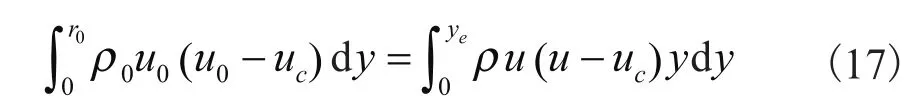
对于射流初始段，АбраМоВИЧ[10]推荐速度分布可采用以下普遍参数剖面来表示：

液滴的分布集中在混合室的轴线附近，随着混合过程的发展向径向扩散。根据Harrell[3]等人的研究结果，对于射流初始段质量浓度的分布，采用线性分布计算。由于假设混合过程没有汽液相的转换，液滴的总含量不变，液滴的质量浓度与混合物的干度等效。假设射流的初始干度为x0，伴随流的初始干度为xc，其液滴质量含量分布可用下面的普遍参数剖面来表示：

对于射流主段，轴对称射流的速度分布用以下普遍参数剖面表示：

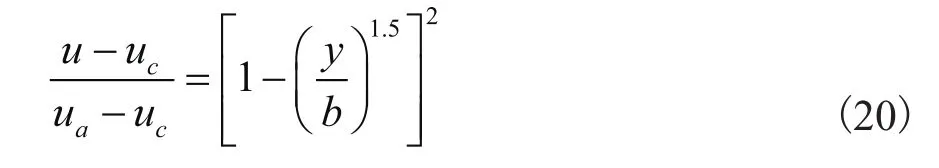
质量浓度分布可以用下式表示：

从喷嘴出来的高速射流喷入喷射器混合室后，引射从吸气室来的引射流体与之混合，射流厚度ye随着流向而增加，当射流发展到喷射器混合室的壁面时，即图2上的ze位置，混合过程终止。即喷射器混合室内的射流混合过程的终止条件为混合段外边界层的纵坐标等于喷射器混合室的半径，即

此时的射流截面上的质量流量m(ze)即为混合后的质量流量，由此喷射器引射比可由下式求出：

2.3 混合流体均匀过程

初始混合过程结束后，由于轴心和边界流体的速度差异，动量传递继续进行，直至流通截面上速度分布均匀。根据质量、动量和能量守恒定律可得：

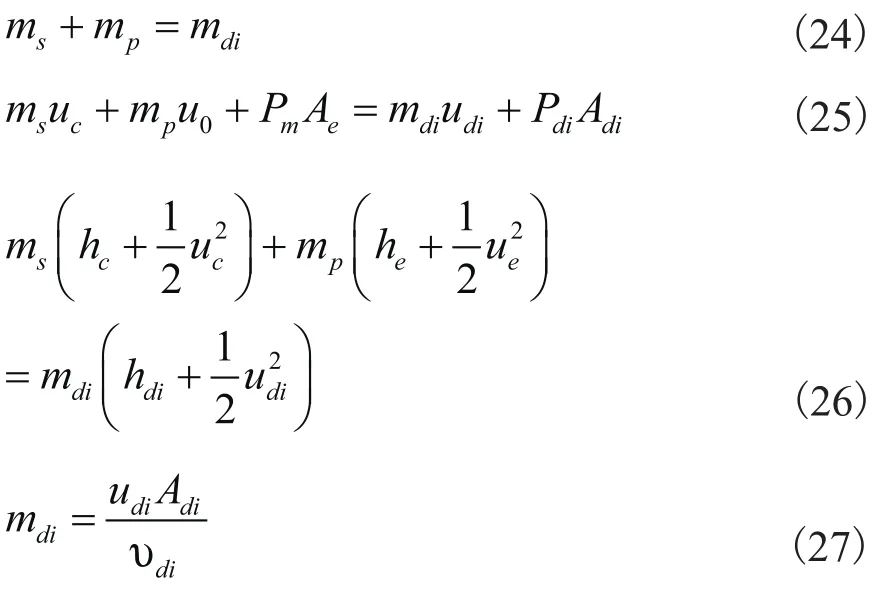
联立式(24)～式(27)即可求得速度均匀后的状态，然后混合射流进入扩压过程。

2.4 扩压过程

喷射器的主流和引射流混合过程完成后，混合流体开始进入扩压过程。如图7所示，流体的扩压过程可看成流体的绝热压缩过程，摩擦等不可逆损失可用扩压室效率来描述。扩压室效率η可定义为：

图7 扩压室内的扩压过程Fig.7 The diffusing process in the diffuser

由扩压过程能量守恒可得：

根据制冷剂物性方程，就可以求得喷射器的出口背压Pde。

3 仿真结果与实验结果对比分析

喷射器的实验测试采用传统压缩/喷射制冷系统实验台进行，原理图如图1(a)所示，所用到的测量仪表及精度如表1所示。

表1 测量仪表量程和精度Tab.1 Range and precision of measurement instrument

工质选用R404A，针对3组工况对所建立的喷射器模型进行了仿真计算和实验验证，喷射器进口过冷度为3℃，冷凝温度分别为40℃、45℃、50℃，蒸发温度从-21℃变化到6℃。测试用喷射器的结构尺寸：喷嘴的喉部直径为2mm，喷嘴出口直径为3.5mm，渐扩段长度为30mm，混合室前段为渐缩形，中间等截面段直径为7mm，扩压段长度为40mm，喷射器出口直径为12mm。

3.1 引射比随蒸发温度和冷凝温度的变化

图8 引射比随蒸发温度和冷凝温度的变化Fig.8 The entrainment ratio varying with the evaporating and condensing temperature

图8给出了模型计算的喷射制冷循环的引射比与实验数据的比较。从图8中可以看出，随着蒸发温度的升高，引射比开始逐渐增大，而后迅速减小，存在一个最大值；随着冷凝温度的升高，引射比增大，这是因为在过冷度一定的情况下，冷凝温度越大，喷射器进口滞止状态的有用能越大。实验测试的引射比与模型预测值相对偏小，这是因为模型没有考虑摩擦等因素的影响，但曲线的变化趋势完全一致。

文献[5]中的图10给出了应用黑箱模型计算出的引射比随冷凝温度的变化曲线，其结论是引射比随冷凝温度增大而减小，这恰好与模型计算出的结果以及实验结果完全相反，充分说明了喷射器内射流混合机理研究的必要性。

3.2 背压随蒸发温度和冷凝温度的变化

图9给出了喷射器出口背压的模型预测值与实验数据的比较。从图中可以看出，喷射器背压随着蒸发温度的升高而升高，但与蒸发压力的差值，即增压效果，却随着蒸发温度的升高而减小，这是因为随着蒸发温度的升高，节流损失减小，可回收的有用能减小；随着冷凝温度的升高，喷射器背压升高。模型的预测值与实际测试值相比稍有偏高，但变化趋势与实测结果完全一致。

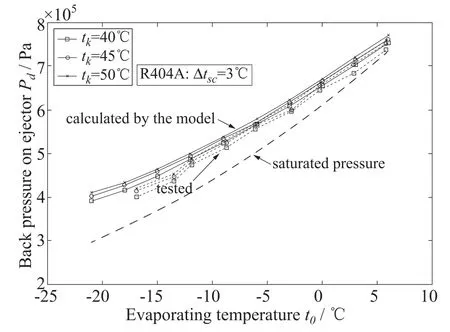
图9 出口背压随蒸发温度和冷凝温度的变化Fig.9 The outlet pressure varying with the evaporating and condensing temperature

4 结论

通过对压缩/喷射制冷系统的喷射器内两相流流动过程的深入分析，对射流发展过程中出现的膨胀波、(斜)激波、射流混合过程、均匀过程、扩压过程建立了数学模型，其中首次将湍流伴随射流理论运用到喷射器内的射流混合过程，使得混合过程的速度和浓度分布得以计算。模型预测结果与实验结果在趋势上显示了良好的一致性，结果表明在压缩/喷射制冷循环中：

1) 冷凝温度越大，喷射器的引射比和出口背压(吸气压力)越大，这预示着节能效果越好；

2) 蒸发温度存在一个最佳值，使得引射比最大。在实际运行过程中建议蒸发温度不宜过大，否则不但引射比会急剧减小，而且吸气压力增大效果也会明显减弱，导致系统运行效率降低。

符号说明

A ——流通面积, m2

b ——射流边界层厚度, m

h ——比焓, kJ.kg-1

P ——压力, Pa

Pd——喷射器背压, Pa

d ——比熵, kJ.kg-1.K-1

tk——冷凝温度, ℃

t0——蒸发温度, ℃

∆tsc——过冷度, ℃

u ——速度, m.s-1

ua——轴线上的速度, m.s-1

uc——射流周围流体速度, m.s-1

u0——射流核心速度, m.s-1

x ——干度

xa——轴线上的干度

yi, ye——射流初始段的内、外边界纵坐标, m

α ——斜激波后速度偏转角, rad

β ——出口射流速度与膨胀波面夹角, rad

θ ——膨胀波后速度偏转角, rad

ω ——出口射流速度与斜激波面夹角, rad

µ ——引射比

υ ——比容, m3.kg-1

η ——扩压室效率

下角标

1,2 ——分别为激波前、后位置

di, de ——分别为扩压段入口、出口位置

e ——喷嘴出口位置

i ——等熵过程

m ——混合段初始位置

p ——主射流

s ——引射流

z ——喷嘴内部激波位置

[1]Kanjanapon Chunnanond, Satha Aphornratana. Ejectors:applications in refrigeration technology [J]. Renewable and Sustainable Energy Reviews, 2004(8): 129-155.

[2]Kemper A B, Harper G F, Brown G A. Multiple phase ejector refrigeration system: U S, 3,277,660 [P].

[3]Harrell G S. Testing and modeling of a two-phase ejector[D]. Virginia Polytechnic Institute and State University,1997.

[4]Hirotsugu Takeuchi, Haruyuki Nishijima, Toru Ikemoto.World's fi rst high ef fi ciency refrigeration cycle with twophase ejector: “ejector cycle” [C]//2004 SAE World Congress Detroit, Michigan, March 8-11, 2004.

[5]刘敬辉, 陈江平, 陈芝久. 压缩/喷射混合制冷系统喷射器设计及其变工况特性探讨 [J]. 应用科学, 2006,24(6): 642-646. (Liu Jinghui, Chen Jiangping, Chen Zhijiu. Ejector in compression/ejection hybrid refrigerator:design and performances[J]. Journal of Applied Sciences,2006, 24(6): 642-646.)

[6]刘敬辉, 陈江平, 陈芝久. 四种双温蒸气压缩制冷循环的制冷性能比较 [J]. 应用科学, 2006, 24(5):538-542. (Liu Jinghui, Chen Jiangping, Chen Zhijiu.COP comparison of refrigeration cycles with two-stage evaporating temperatures[J]. Journal of Applied Sciences,2006, 24(5): 538-542.)

[7]邓建强, 姜培学, 卢涛, 等. 跨临界CO2蒸气压缩/喷射制冷循环理论分析 [J]. 清华大学学报. 自然科学版, 2006,46(5): 670-673. (Deng Jianqiang, Jiang Peixue, Lu Tao,et al. Theoretical analysis of a transcritical CO2vapor compression / ejection refrigeration cycle[J]. Journal of Tsinghua University. Science and Technology, 2006,46(5): 670-673.)

[8]孔珑. 可压缩流体动力学 [M]. 水利电力出版社, 1991.(Kong Long. Compressible fluid dynamics[M]. China Water Power Press, 1991.)

[9]Liu J H, Chen J P, Chen Z J. Critical Flashing Flow in Convergent-divergent nozzles with initially subcooled liquid [J]. International Journal of Thermal Sciences,2008(47): 1069-1076.

[10]谢春象. 湍流射流理论与计算 [M]. 科学出版社, 1975.(Xie Chunxiang. Theory and computation of turbulent jet[M]. China Science Press, 1975.)