单边接触悬臂梁振动特性研究
2010-07-31张春霞
张春霞
(天津市渤海职工学院,天津 300000)
引言
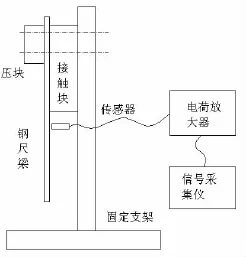
图1 实验装置简图
接触对工程结构的动态行为影响十分复杂。一方面因接触碰撞而产生的强烈振动,往往成为许多工程结构失效的元凶,也给传统结构振动分析及其分析结论的实际应用造成很大影响;另一方面机械系统的特点是由多个零件通过各种方式联接起来的一个系统。机械系统的性能分析除了零件的性能分析以外,零件之间的联接特性的分析也是一个重要方面。零件之间的联接性能分析,本质是一个接触问题的分析,是机械结构非线性分析的一种典型类型。 线性系统的模态分析技术是了解线性结构振动特性的一个重要手段,已经广泛应用在结构动力修改、优化设计、故障诊断、状态检测等诸多领域。近年来,以非线性动力学理论为基础的非线性模态分析逐渐成为非线性振动研究中的热点之一。其原因是机械工程中存在着大量的接触问题,传统的线性模态分析技术无法得到准确的结果。解决机械系统中的非线性振动问题,首先要面对的就是如何处理结构间的接触振动问题。
本文主要采用实验分析的方法进行研究,重点是研究单边接触约束悬臂梁在阶跃位移载荷激励和敲击激励下的系统振动特性。利用时频分析法对振动信号进行分析,探索在接触问题中振幅、时间和频率之间的相互关系,为机械结构参数的设计与优化提供理论依据。
1 实验装置
1.1 悬臂梁参数
悬臂梁尺寸:252.5×26.7×0.8(mm)
理论固有频率有限元计算结果:
11.856 ,74.297,208.03,407.65,673.85(Hz)
1.2 单边接触约束块参数
接触块:90×40×50(mm)
接触约束有效长度:51.5(mm)
1.3 测量系统参数
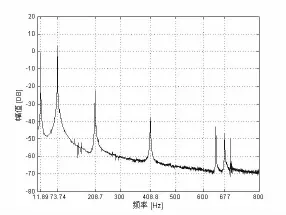
图2 悬臂梁频谱图
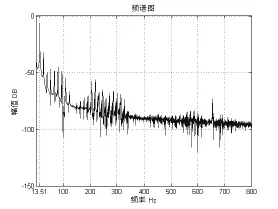
图3 阶跃激励频谱
涡流传感器:BENTLY NEVADA PROX-IMITOR SENSOR,测头直径6mm,比例系数7.87mV/um
信号采集仪:NEC omniaceII RA1200
2 实验过程
测量时将位移传感器固定在悬臂梁的根部(距梁底端165mm处),以测量此处的位移响应,波形通过信号采集仪记录并以SCV格式输出数据。通过Matlab软件读入数据,然后进行后期的信号处理。
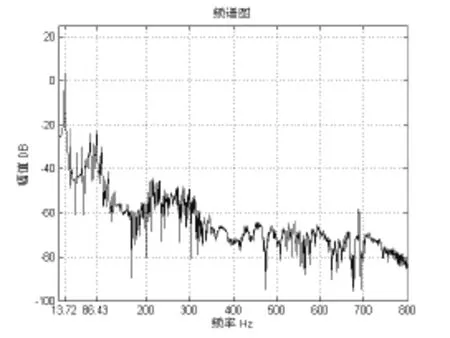
图4 敲击激励频谱
实验中主要测量单边接触约束悬臂梁在阶跃位移激励和敲击激励时的响应,以及无接触约束的悬臂梁在敲击激励时的响应阶跃激励的加载过程:在距梁端部50mm处使梁在垂直方向有7mm的偏移,然后突然释放使其自由振动;敲击激励的加载过程:在梁的底端沿垂直方向用小锤敲击,使其在很短的时间内受到冲击力载荷的作用,梁在该冲击力的作用下自由振动。
3 数据分析处理
3.1 悬臂梁固有频率的测试
通过对测得的数据进行傅立叶变换,根据其频谱图(如图2所示)可得出悬臂梁系统的前五阶固有频率。实验测得的数值与理论算得数值很接近,最大相对误差都不超过理论值的1%。
3.2 不同激励条件下频谱比较
3.2.1 阶跃激励
对单边接触约束的悬臂梁阶跃激励响应数据进行傅立叶变换,频谱图如图3所示。从图中可以看出,在单边约束时候主要以基频13.51Hz振动为主,另外在基频的整倍频处也有较大的振幅。产生这种现象的主要原因是,在接触振动中,梁跟边界发生接触的时间是周期性的,又由于梁的第一阶振动幅度最大,因此这种接触边界对梁来说,相当于给其施加周期性激励且激励频率以第一阶频率为主,所以其激励响应主要以基频为主,在基频的整倍频附近也有较大的振幅。

图5 阶跃激励时频谱
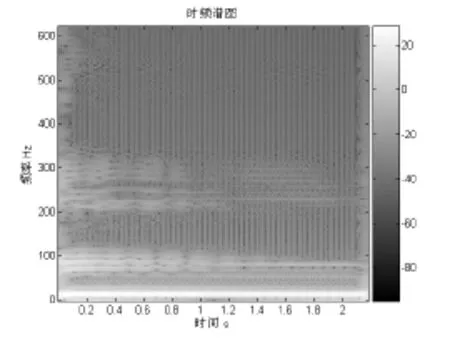
图6 敲击激励时频谱
3.2.2 敲击激励
对单边接触约束的悬臂梁敲击激励响应数据进行傅立叶变换,频谱图如图4所示。
从图中可以看出,在敲击激励时候主要以基频13.72Hz振动为主,基本同阶跃激励的基频一致,另外在基频的整倍频处同样也有较大的振幅。在150Hz以后的振动与阶跃激励有明显的不同,这是由于敲击激励激起了更多的高频成分,系统的振动在高频范围内表现出较大的波动。
由两种工况比较知,结构在单边接触约束的边界条件下,随着激励频率的增加,系统各阶频率的振幅波动逐步增加,且高频成分也增加。但是当边界条件固定不变时,系统的基频也保持不变;接触边界抑制了一些高频成分,使其表现成在高频附近有起伏不等的波动。
3.3 不同激励条件下时频谱比较
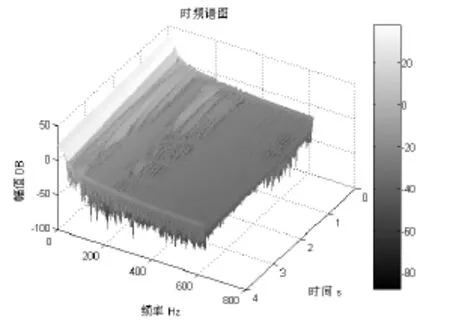
图7 阶跃激励三维时频谱
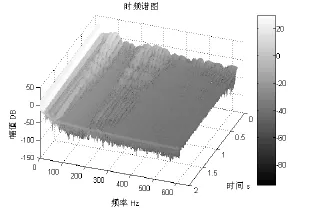
图8 敲击激励三维时频谱
利用Matlab时频分析工具箱中的短时傅立叶变换函数(TFRSTFT函数),分别对阶跃响应信号和敲击响应信号进行短时傅立叶变换,获得其时频分布谱,如图5~图9所示。从图中可以明显看出,高频成分随着时间的增加而逐步衰减,在0~100Hz与200~300Hz的频段内振幅较大,在100~200Hz频段内振幅较低,这种在不同频段内的较大波动跟接触边界息息相关;不同频率成分的振动幅值随着时间变化的幅度不同;从含有接触边界约束与无边界约束的悬臂梁三维时频谱比较可以看出,两种条件下的共振频率不同。
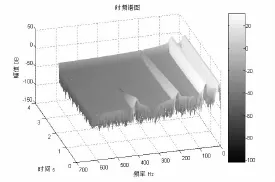
图9 悬臂梁三维时频谱
4 结论
综上,单边接触约束的悬臂梁振动有如下特点:(1)由于在两种不同外界激励下,系统的振动响应基频与悬臂梁振动响应基频基本相同,因此可以认为这种单边接触约束条件,并不改变系统的质量矩阵和刚度矩阵,跟位移约束的效果不同,实验结果表明这个数值模型是正确的。(2)在相同边界条件下,不同外界激励频率时,系统响应频谱都以悬臂梁的固有频率及其倍频成分为主。在前几倍频处(如2、3倍频)也有较明显的振幅,随着倍数的增加,振幅逐渐减小,呈现出共振频率聚集的现象。
[1]L.科恩,白居宪.时-频分析:理论与应用[M].陕西:西安交通大学出版社,1998,年3月第一版.
[2]郭小明,赵慧麟.工程结构接触问题的研究及进展[J].东南大学学报(自然科学版).2003,9月,第三卷第5期:577-582.
[3]王济,胡晓.Matlab在振动信号处理中的应用[M].北京:中国水利水电出版社,2006年1月第1版.
[4]张华,赵登峰.间隙约束悬臂梁振动特性研究[J].广西轻工业,2007年4月,第4期(总第101期):51-52.
[5]李润方,龚剑霞.接触问题数值方法及其在机械设计中的应用[M].重庆:重庆大学出版社,1991.
[6]李香莲.机械振动信号的时频分析[J].山东工程学院学报,1999年9月,第13卷第3期:42-47.
[7]崔秀英.悬臂梁受迫振动频谱分析[J].振动测试与诊断,1995年04期.
