滑动层对桥上CRTSⅡ型板式无砟轨道无缝道岔群的受力影响

2010-07-30张国栋陈小平

铁道建筑 2010年11期

宋杨，王平，张国栋，陈小平

(西南交通大学土木工程学院，成都 610031)

桥上铺设CRTSⅡ型无砟轨道无缝道岔是桥上无缝线路、无缝道岔、桥上CRTSⅡ型无砟轨道技术的综合运用。桥上铺设CRTSⅡ型无砟轨道无缝道岔时，底座板与桥梁纵向相互作用关系较为复杂，主要通过两种途径:一是底座板与桥梁间的滑动层摩擦作用;二是桥梁墩台固定支座处的剪力齿槽。其中滑动层的设置是桥上CRTSⅡ型板式无缝道岔的方案的关键技术之一，具有降低摩擦、减小桥梁伸缩对无砟轨道影响的作用，但在线路运营中，滑动层可能因磨损、桥面或底座板不平整等原因失效，并且无法修复，摩擦系数变化很大，从而引起整个系统结构受力和位移的重新分布。因此，充分掌握这种复杂关系，分析无缝道岔、无砟轨道、桥梁及其墩台的受力特点，对于进行相应的结构设计，具有十分重要的意义。

本文拟运用空间有限梁单元理论，建立桥上CRTSⅡ型无砟轨道无缝道岔的岔—板—桥—墩一体化模型，分析滑动层对钢轨、道岔、轨道板、底座板、固结机构与墩台等结构部件温度附加力的影响。

1 计算模型与参数

1.1 计算模型

与桥上CRTSⅡ型无砟轨道相比，桥上CRTSⅡ型无砟轨道无缝道岔由于道岔结构的添加更为复杂，相邻股道间的纵向力不仅通过桥梁相互作用，还可能通过道岔板或底座板横向连接，道岔板与底座板间除了填充砂浆外，还通过锚筋相互作用，并且道岔本身存在伸缩区(尖轨和心轨的可动部分)，即使桥梁不伸缩，钢轨的温度变化幅度也会引起道岔与下部基础间的相互作用。根据桥上CRTSⅡ型无砟轨道无缝道岔纵向传力特点，建立图1所示岔—板—桥—墩一体化纵向力计算模型。模型对道岔结构作如下假定:道岔尖轨与可动心轨前端可以自由伸缩，不考虑辙叉角大小的影响;考虑间隔铁阻力对钢轨伸缩位移的影响，间隔铁阻力与钢轨间的位移呈非线性关系;考虑辙叉跟限位器在基本轨与导轨间所传递的作用力，设道岔铺设时限位器字母块居中，间隔为7～10 mm，当子母块贴靠时，限位器阻力与两钢轨间的相对位移呈非线性关系。

1.2 计算参数

轨道板标准区段宽2.55 m，高0.2 m，轨道板岔区宽5 m，高0.2 m，混凝土强度等级为C50;底座板标准区段宽2.95 m，高0.19 m，底座板岔区宽5 m，高0.19 m，混凝土标号为C40;钢轨为60 kg/m钢轨，弹性模量为2.06×105MPa;扣件阻力为双线性，当水平位移为0.5 mm时，由扣件产生的纵向摩擦阻力最大值取为30 kN/m;固结机构的刚度取为1 000 MPa/mm;端刺纵向刚度取为100 MPa/mm;滑动层的摩擦阻力是非线性的，极限摩擦阻力对应的位移一般为0.5 mm。

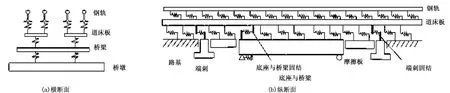
图1 岔—板—桥—墩空间一体化计算模型

对于桥上CRTSⅡ型无砟轨道无缝道岔进行温度力计算时，不仅要考虑桥梁温度变化幅度，还应同时考虑钢轨、道岔板和底座板的温度变化幅度，以反映整个系统在温度荷载作用下的最不利状态，为系统的结构设计提供基础荷载。根据当地气温，底座板降温54℃，轨道降温24℃，桥梁降温30℃，钢轨降温48℃。

图2 桥梁与无缝道岔的布置形式

某高架桥上铺设6组18号无缝道岔，桥梁与无缝道岔的布置形式如图2所示。桥梁在温度荷载作用下产生伸缩位移，使得轨道产生纵向附加作用力，力的大小与桥梁伸缩位移、桥梁与轨道间的摩擦阻力有关。利用岔—板—桥—墩一体化模型，分析桥梁产生温度变化时轨道、桥梁相互作用，以及底座板与桥梁间不同摩擦系数对伸缩力的影响。本文分析滑动层摩擦系数为0，0.3，0.7，1.0情况下的结构物各部分的受力特点。

2 计算结果

2.1 滑动层摩擦系数对钢轨的影响

滑动层摩擦系数分别取为 0，0.3，0.7和 1.0，最大钢轨应力和相对位移见表1，摩擦系数为0和1.0时，钢轨应力、相对位移曲线如图3所示，摩擦系数为0.3和0.7时钢轨应力、相对位移曲线与图3相似，但数值略有不同。

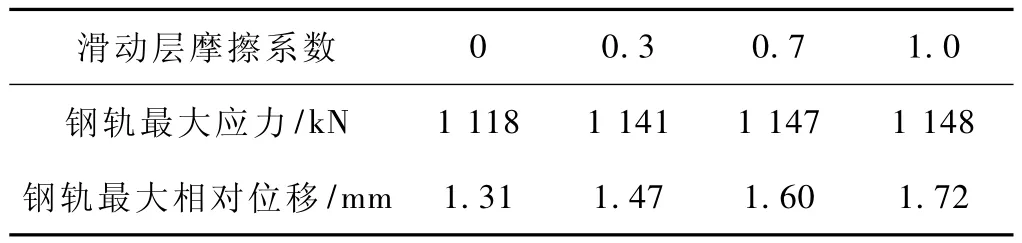
表1 滑动层摩擦系数对钢轨应力和相对位移的影响

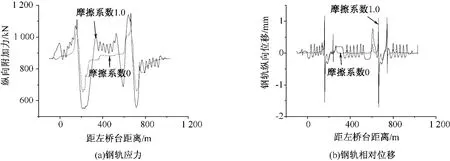
图3 钢轨应力和相对位移

图3表明，当摩擦系数为0时，除在道岔处有明显起伏外，钢轨应力、相对位移曲线较为平顺，滑动层摩擦系数从0增加到1.0，曲线随桥梁布局变化的规律更明显并且变化幅度更大，在道岔区的变化幅值也更明显，表明随着摩擦系数的增大，桥梁伸缩对上部轨道结构的影响越大;另外钢轨相对位移在道岔首尾端处发生突变，这是因为普通轨道板与道岔板是不连续的，在降温工况时带动钢轨向两端收缩。从表1可看出，钢轨最大应力和相对位移也随着滑动层摩擦系数的增大而略有增大，这是由于钢轨受到了不断增大的桥梁伸缩附加力。

2.2 滑动层摩擦系数对轨道板、底座板的影响

滑动层摩擦系数分别取为 0，0.3，0.7和 1.0，轨道板、底座板最大纵向力见表2，摩擦系数为0和1.0时，轨道板、底座板纵向力分布曲线如图4所示，摩擦系数为0.3和0.7时，轨道板、底座板纵向力分布曲线与图4相似，但数值稍有差异。

表2 滑动层摩擦系数对轨道板、底座板的影响

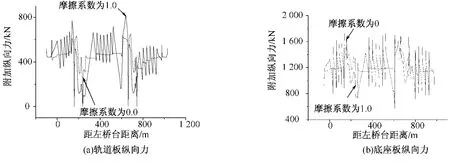
图4 轨道板、底座板纵向附加力

从图4可以看出，轨道板、底座板纵向力分布规律与钢轨应力相似，纵向力总体分布规律为典型的温降附加力分布规律，即在梁跨的活动端出现极大拉力，梁跨的固定端出现极小拉力，并且在连续梁范围内出现最大和最小拉应力;由于轨道板、底座板与桥面联接密切，随着滑动层摩擦系数的增大，纵向力变化的幅度增加。从表2可以看出，轨道板、底座板最大纵向力变化不大，但是图4显示，摩擦系数较大时，各桥梁跨度极大值与最大值相似，可见滑动层摩擦系数增大对轨道板、底座板受力不利。

2.3 滑动层摩擦系数对固结机构、墩台顶的影响

滑动层摩擦系数分别取为 0，0.3，0.7和 1.0，轨道板、底座板纵向力分布曲线如图5所示，摩擦系数为0.3和0.7时，轨道板、底座板纵向力分布曲线与图4相似，但数值稍有差异。

从图5可以看出，随着底座板与桥梁摩擦系数增大，作用在底座板上的摩擦附加力就越大，因此作用在简支梁墩台固定支座附近的固结机构所传递的纵向力也就越大，由于连续梁结构较为复杂，并且其上普通轨道板与道岔板不连续，固结机构受力变化规律不明显。墩台顶的纵向水平力变化不大，这是由于增大摩擦系数，道床板通过摩擦传给桥梁的纵向力虽然增大了，但固结机构所传递的作用在底座板上的摩擦附加力与之近似一对平衡力系，由梁面摩擦力和固结机构传递的纵向力总和仍然相当。

2.4 滑动层摩擦系数对道岔位移和受力的影响

取线路正线上四组道岔，道岔编号按从下到上、从左到右排列，直尖轨尖端相对曲基本轨、长心轨尖端相对翼轨的位移见表3，1号道岔各工况下传力部件所受纵向力如图6所示。

表3 直尖轨尖端、长心轨尖端相对下部基础位移 mm

图6 1号道岔传力部件纵向力

表3表明，两种位移随摩擦系数增大，都依次减小，由于模型假设道岔尖轨与可动心轨前端可以自由伸缩，道岔尖轨跟端、心轨跟端位移也同样减小。从图6可以看出，1号道岔转辙器直股、侧股限位器纵向力变化明显，摩擦系数为1.0时，限位器受力微小，说明子母块刚好开始贴靠，随着摩擦系数减小，子母块贴靠更加紧密，限位器受力迅速增大;由于心轨跟端位移变化不大，1号道岔长翼轨直股、侧股间隔铁纵向力仅有微小变动，因此滑动层摩擦系数增大对道岔转换设备、结构传力部件受力是有利的。