地震对有砟轨道横向变形影响分析

2010-07-30徐彩彩赵坪锐刘学毅

铁道建筑 2010年6期

徐彩彩，赵坪锐，刘学毅

(西南交通大学土木工程学院，成都 610031)

我国是一个多地震国家，强烈的地震导致路基变形破坏、铁路线路弯曲、钢轨被拉断等，严重影响着铁路的安全运营。

《铁路工程抗震设计规范》中，抗震设计内容仅仅局限于线路、路基、挡土墙、桥梁和隧道抗震设计。汶川大地震发生后，铁道部和中国铁道协会通过对汶川大地震的经验总结，借鉴先进的抗震设计理念和方法，重点考虑对线路、路基、桥梁、隧道和轨道进行修订，首次在铁路工程抗震设计中提出轨道抗震设计，指出应增加轨道抗震设计内容。轨道抗震设计标准应包含轨道抗震设计目标、抗震设计原则、有砟轨道抗震设计重点、无砟轨道抗震设计重点和艰险山区轨道抗震设计等相关内容。

钢轨“蛇”形弯曲作为轨道震害形式之一不容忽视。钢轨弯曲变形大多出现在路基沉陷、石砟沉落坍塌的处所，但在轨道结构标准较低的情况下，即使路基未受破坏，在纵向和横向地震力作用下，钢轨也可能丧失稳定性产生严重弯曲。本文旨在研究震后路基未损坏情况下，不同烈度地震对有砟轨道横向弯曲变形的影响，以及地震作用下不同曲线半径轨道和直线轨道弯曲变形的特点，初步建立地震烈度等级和轨道弯曲变形程度之间的对应关系。

1 计算方法

1.1 计算模型

采用弹性点支承有限长度梁模型，枕跨取30跨，钢轨和轨枕简化为梁单元，扣件为线性弹簧元件，路基为非线性弹簧元件，以地震时地面水平加速度时程记录作为输入，研究轨道弯曲变形特点及规律。地面加速度时程记录分别采用美国 EI－Centro水平地震波(适用于二类场地)和Loma Prieta水平地震波(适用于三类场地)记录，其速度时程曲线见图1。

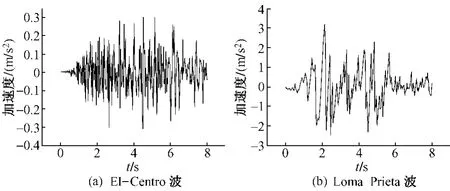
图1 水平地震波

根据国家地震局批准的地震烈度表，基本烈度为5～10度时，地面运动的最大水平加速度分别为0.031 g、0.063 g、0.125 g、0.250 g、0.500 g、1.000 g，计算中必须将实际地震记录的峰值折算成所需的基本烈度。

1.2 计算方法

本文采用动态时程分析法，直接计算结构随时间而变化的地震反应。该方法既考虑了地面的振幅、频率和持续时间三要素，又考虑了结构的动力特性，是目前抗震设计中普遍采用的较为先进的直接动力计算方法。多自由度体系在地面运动下的振动方程为式中，分别为体系的水平位移、速度和加速度向量;为地面运动的水平加速度;［K］、［C］、［M］分别为体系的刚度矩阵、阻尼矩阵和质量矩阵;［I］为指示矩阵。

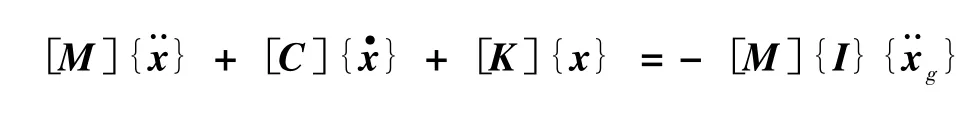
本文中，时程分析法采用数值法 Newmark法求解。

1.3 计算参数

道床纵向阻力与横向阻力根据由中国第四勘察设计院主编的《铁路无缝线路设计规范(送审稿)》中铁四院在汉丹线上的测试结果进行取值，Ⅲ型枕纵向阻力r与位移f的方程式为

r=3.24－7.21f+17.92f3/4

道床横向阻力是防止胀轨跑道、保持轨道稳定的重要因素。它是由轨枕两侧及底部与道砟接触面间的摩阻力和枕端的砟肩阻止横移的抗力组成。其中，道床肩部占30%，轨枕两侧占20% ～30%，轨枕底部占50%。在计算中假定，轨枕位移<20 cm时，Ⅲ型轨枕横向阻力q与位移f满足

q=25.11－1 012.87f+1 014.1f3/4

当轨枕位移>20 cm时，道床肩部阻力逐渐减小;当轨枕横移达到40 cm时，肩部阻力完全丧失，同时，轨枕两侧及底部与道砟接触面间的摩阻力也逐渐减小;当轨枕横移量超出轨枕本身长度时，横向阻力全部消失。

钢轨采用60 kg/m轨，轨枕为Ⅲ型枕，扣件横向刚度取50 kN/mm，纵向刚度取16 kN/mm。

2 计算结果及分析

2.1 震后轨道变形图

场地不同，地震波不同及线路曲线半径不同等情况下，同样的轨道结构变形形状及变形值都不相同。取其中的30跨轨枕轨道，施加加速度峰值相同的不同地震波，各轨道变形如图2所示。通过建模计算，得出的轨道变形图和地震后现场拍摄的照片类似。在地震作用下，轨道或整体偏向一侧，或出现类似正弦形变形等。由于地震波的随机性，轨道的变形形状也变化多样。

2.2 美国EI-Centro波作用下轨道横向变形分析

线路曲线半径分别为400 m、1 000 m、5 000 m及线路为直线时，不同地震烈度地震波所对应的轨道震后变形见图3。轨道变形最大值列于表1。

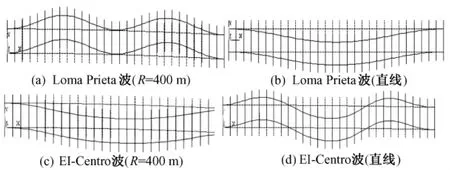
图2 30跨轨枕轨道变形

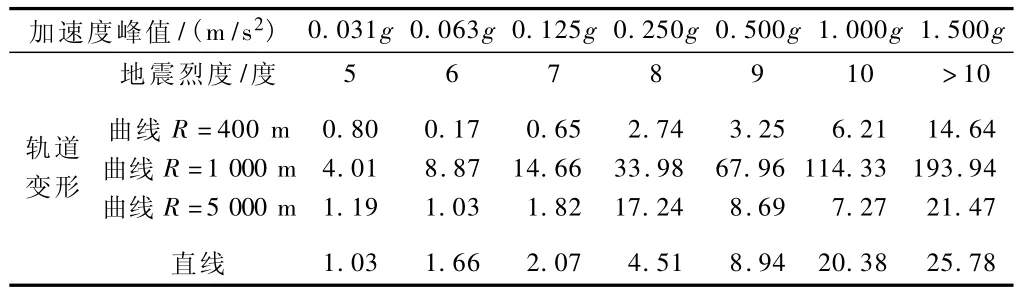
表1 轨道横向变形最大值mm

图3 El-Centro波作用下轨道横向变形

从图3及表1可知:

1)轨道横向变形随着地震烈度的增大而增大。

2)随着曲线半径的增大，地震作用下轨道变形基本呈先增大后减小的趋势。

《铁路线路维修规则》规定，轨道轨向应满足:直线方向必须目视平顺，用10 m弦测量，正线上正矢不超过4 mm，站线及专用线不得超过5 mm;曲线上轨道的方向偏差是用20 m弦测量圆曲线或缓和曲线上的正矢与计算正矢的差。当地震烈度为5度及5度以下时，轨道的横向变形较小，基本不影响列车的运行。对于半径为1 000 m的轨道，当地震烈度为6度及7度时，横向位移较大，应进行轨道检测，必要时需对轨道进行维修;当烈度达到8度以上时，轨道变形明显变大;当烈度达到10度以上时，轨道破坏严重。对于直线和半径400 m轨道，当烈度在8度以下时，横向变形较小，基本不需维修;当地震烈度达到9度以上时，轨道变形较大，需维修后尚可考虑通车运营。

2.3 Loma Prieta波作用下轨道横向变形分析

线路曲线半径分别为400 m、1 000 m、5 000 m及线路为直线时，不同地震烈度地震波所对应的轨道震后变形见图4。轨道变形最大值列于表2。

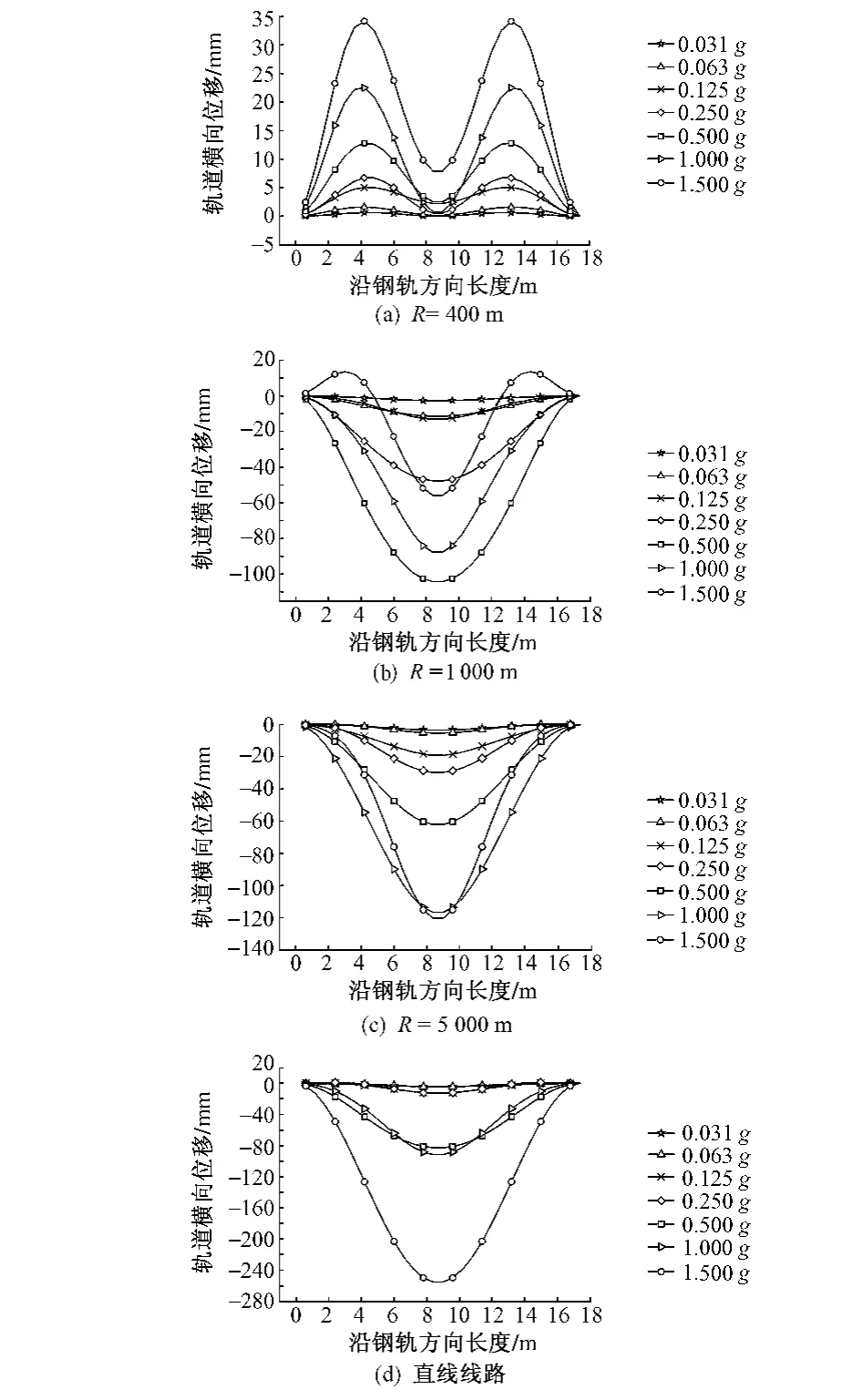
图4 Loma Prieta波作用下轨道横向变形

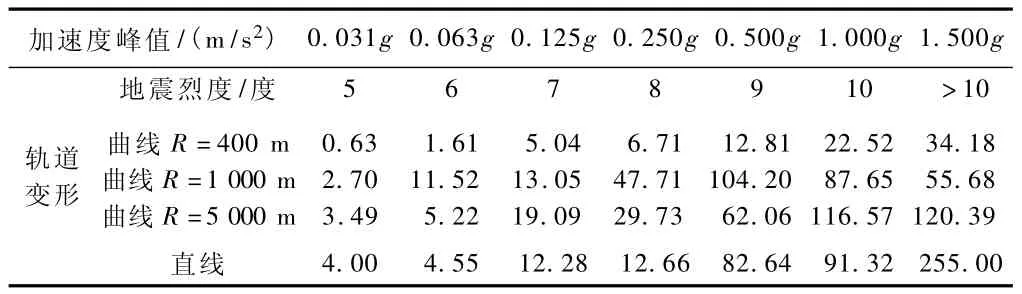
表2 轨道横向变形最大值 mm

从图4和表2可知:

1)轨道横向变形随着地震烈度的增大而增大。

2)当地震烈度为5度及5度以下时，轨道的横向变形较小，基本不影响列车的运行。当地震烈度为6度及7度时，轨道横向变形大多达到4 mm以上，震后应进行轨道检测，必要时应实施线路维修。当烈度达到8度以上时，不同半径的轨道变形差别较大，曲线半径为400 m时，变形在几厘米内，尚可以维修;当半径较大的线路，变形超过10 cm，线路已不易维修，需重新更换轨道。

3)随着轨道曲线半径的增大，地震作用下的轨道横向位移有先增大后减小的趋势。