三种键盘乐器的声学构造

编译/程伊兵

（中国音乐学院，北京 100101）

1 背景知识

键盘乐器（带键盘的弦鸣乐器）以一开始冲击琴弦使其自由振颤，最终抑制这些自由颤动的、琴键操作的机械设备著称。这些击打和阻尼设备的形状、尺寸、材质和功能的差异，产生了音符开始和结尾的大部分特质变化。同时，这些差异也影响着琴弦自由振动时的音色，因为最初的冲击决定后继波形的颤动。其他声学因素有琴弦的硬度、低音弦的包裹材料、弦支撑处音色的渐弱（the gradual damping of tone at the string supports）、每个琴键的弦数、琴弦支撑结构的声学属性，以及某些情况中的被动共振琴弦效果。

楔槌钢琴（clavichord）、羽管键琴（harpsichord）和钢琴（piano）大约都是横置在一个平面上的，各自具备经校准的琴弦系统。每根琴弦都有张力地安置在琴弦支撑结构上，在挂弦钉（hitch-pin）和位于弦轴板（pinblock）上调律时可以旋转的调音钉（tuning-pin）之间。通常在这两组弦钉之间靠近它们的地方，琴弦别靠在一个滑动接触点上。这两个中间点之间的距离决定了经调校的琴弦的颤动区间。如果琴弦具有完美柔韧性的话，各琴弦都可以按泛音列之频率自由颤动。因为金属弦具有一些硬度（微似条棒），弦振动的自然泛音列略呈不谐和，但是可以被听到。迄今为止的研究表明，非谐和度是音色的重要特质。非谐和性也导致最适宜的乐器调律比例比2:1八度关系伸展少许（即低音低、高音高）。

在键盘乐器中，演奏琴键的动作导致了能动的弦激励。有些冲击声立即发声于冲击点上，更多则需通过弦振动来发声。这是一个“起因（cause）”的声音。三种主要键盘乐器的冲击和结果弦激励的特征都不同，但在每个情况中，至少是经校准琴弦的某一部分的形状突然改变了。在激励事件之后，琴弦在两接触点之间上下移动，其形状的变化是脉冲波形。这是“结果（effect）”声音。

脉冲波形的一部分在琴弦接触点被来回地反射，致使琴弦颤动以及结果音高的延留，但是每次反射中所贮存波形能量中的一部分被转移最终导致音符静止。这个在波形每次往返的末端被转移的颤动能量，振动着支撑机构，特别是通过音板（soundboard）大部分声音能量进入到空气中。其中，仅有很小一部分直抵空气的声学能量来自琴弦的运动。琴弦一般同时以很多频率在颤动。因为这些频率几乎落在泛音列中，所以听者听到的是以该系列中最低频率为音高的一个音符。复杂音色声音中产生的各频率间的相对关系在很大程度上决定音符在其“结果”阶段的音色。这取决于冲击琴弦时的脉冲形状、支撑结构的接触点对弦振动各频率的响应以及构造将振动转换为声音中各频率的转换效率。

2 楔槌钢琴

楔槌钢琴是典型的矩形琴箱，键盘占长的一边的2/3。琴弦以水平方向绷在琴板左边的挂弦钉与右边的调音钉之间。右端有一个支撑弦马（有时分段）的小水平音板，为每根琴弦提供一个下定位（downbearing）接触点。长低音弦靠近键盘，短高音弦在尾端附近。每个演奏琴键被放在平衡枢轴（balance-rail）上，受位于垂直槽中的后舌簧（rear tongue）的控制。

楔槌钢琴动作的独特机械功能是正切（tangent），一个与键尾扩展区有关的楔形铁片或铜片。当琴键被按下时，楔槌升起并直接撞击琴弦，直到琴键被释放，楔槌一直保持与琴弦的接触。楔槌由此发挥两方面功能：在不需要任何中介装置作用的帮助下，其撞击制造出琴弦的激励；同时，为其所关联的琴弦提供了第二个下定位点，由此定义了振动琴弦区间的长度，控制其音高频率。换言之，被调谐区间的击点（striking point）与界点（termination point）是相同的。

在很多楔槌钢琴中，通过将楔槌布置在琴弦的不同位置，琴弦被很少组合在一起使用的多个音符公用（如C和C#）。这样的乐器被认为是有品的（fretted）楔槌钢琴。其他的则为了更大的音乐多面性而采用单独琴弦。

键载（key-borne）楔槌与被撞击琴弦的持续接触带给楔槌钢琴一种其他键盘乐器无法获得的音乐效果“揉音（Bebung）”。当演奏者周期性地改变琴键压力时（下键敲击后），使琴弦张力波动，产生音高颤动。

在楔槌击点与挂弦钉之间有布条交织在琴弦之中。它们迅速止住未适当校准的、到击点左边的这段琴弦的颤动。当楔槌与琴弦的接触被断开，它们也止住整个琴弦的颤动，不再需要单独的止音动作。

楔槌钢琴存在一些固有的声学优势与缺陷。金属锋在弦端的撞击激发出全频域的频率。脉冲波形在更猛烈的打击下加强，带来良好的动态范围。然而，楔槌力度与音板都很小，因此，楔槌钢琴的输出音量受限制。从琴键到演奏者手指到琴弦的直接联系容许“揉音”颤动，但其同时也产生使音符时值变短的机械衰减。

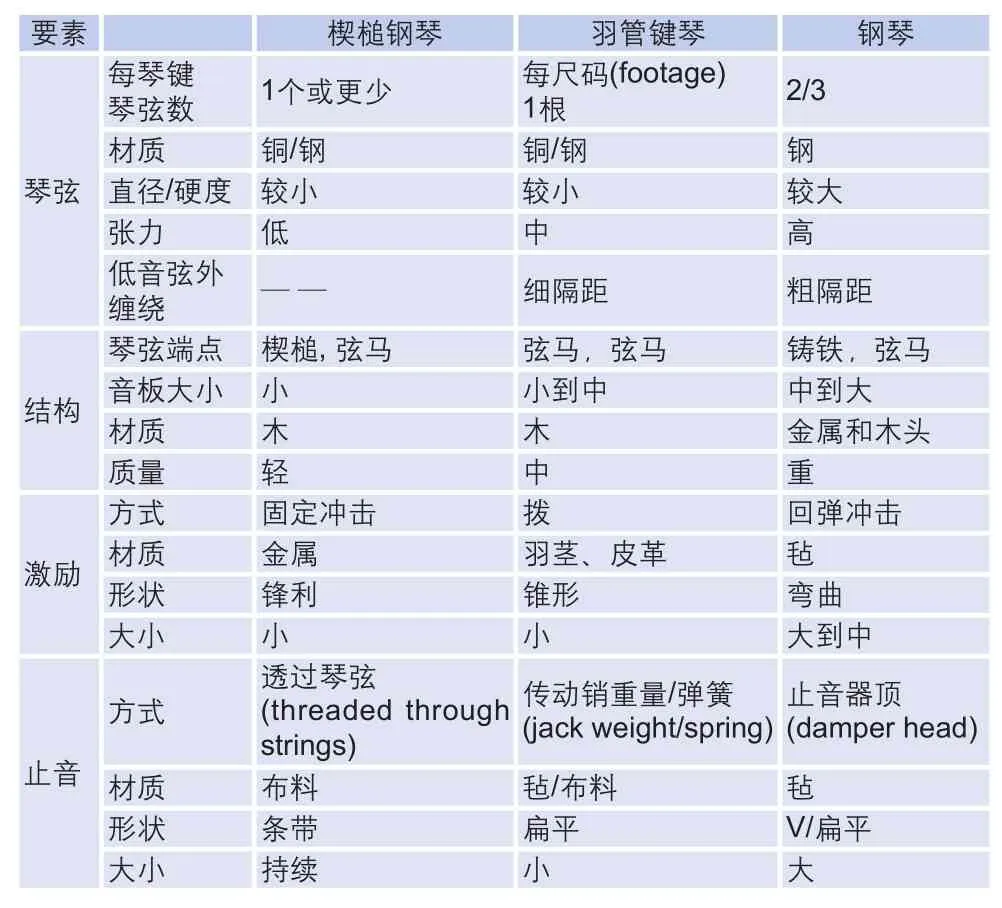
表1 三种主要键盘乐器的构造和机械差异

3 羽管键琴

羽管键琴家族有三种琴弦排列方式：通常为水平张伸；在小矩形维吉那琴（virginals）中，琴弦与楔槌钢琴一样十字互交；在小型翼状（wing-shaped）斯皮耐琴（spinet）中，琴弦从正好在键盘后的调音钉非垂直的延伸到挂弦钉，成一排弯曲至键盘右侧。这种形状上的差异以及附加的长低音弦使得羽管键琴成为体积更大的乐器。更大的音板可以产生更多的声音效果以及更全的音色。

三种排列方式的琴弦，都是被所衔接的羽茎或拨片向上的拨奏激活的，之后释放琴弦。拨片发射自被装在枢轴上的演奏琴键所支撑的，导向滑动的窄垂直传动销（vertical jack）的中央舌簧（central tongue）部分。

在大型羽管键琴中有两套或更多套琴弦以及两副及更多副键盘。因此，同一键负载的不同拨片可以同时拨奏在不同套中的八度相关的不同琴弦。同一琴弦也可以被不同键盘的拨片沿其长度在不同位置上拨奏。拨片与琴弦端点的距离越短，音符的更高、更亮的分音就越强；距离得越远，则低音分音更强。拨片可以是羽茎、皮革、木头、金属或塑料。材质更坚硬、边缘更锐利，带来的音色就更明亮。

羽管键琴与其他键盘乐器最重要的声音区别是音符的开始拨奏。小的锋利的拨片边缘，随着拨片经过琴弦的突然释放，制造出具有丰富高音分量的琴弦波形，赋予羽管键琴明亮的音色特点。与楔槌钢琴对照，琴弦激励者立即离开了琴弦，不能吸收琴弦的振动以缩短音符时值。演奏琴键释放时，拨片的回位往往会产生一个微弱的二次弦激励。该冲击被回位插簧（returning jack tongue）的绕轴旋转最小化了。虽然结果声音是羽管键琴音色的特质，但其发生得很及时，在销载止音器（jack-borne damper）抵达琴弦的时候，听起来就像是止音动作的一部分。

4 钢琴

第一台克里斯多佛利（Cristofori）钢琴是用带有摆轮（escapement）的上击锤（upstriking hammer）动作代替了拨弦动作的羽管键琴。这释放了皮革包裹的榔头，相对于楔槌钢琴的正切动作（tangent action），在压紧琴弦之前，容许它敲击琴弦并很快恢复。击锤动作赋予钢琴全部可控的强弱渐变级别，开创出以往仅有声音太弱不能与其他乐器一起演奏的楔槌钢琴才能做到的，键盘力度表现的音乐会形式。克里斯多佛利是三角钢琴的前身。钢琴榔头比既往的楔槌和拨片更大、更圆，给予琴弦的脉冲形状更大、更圆。这带给低频分量更多的能量，而高频能量则更少，使得钢琴比羽管键琴音色更丰满。对需要明亮的高音而言，榔头更小、更锐利。

之后，通过简单地将上击锤动作与源自楔槌钢琴的弦振动系统相结合，开发出一种小型钢琴。但是因为这种钢琴太小，其声音很微弱。此外，还为这种流行的矩形或“方”钢琴乐器发明了许多不同的机械动作装置。

榔头代替了拨片使得每个音符容许多个共面同度琴弦，这在羽管键琴中是不可能实现的。这种提升了的声音响度导致的其他优势将在下面讨论。为立式钢琴的琴弦系统开发出了前击锤（forward-striking hammer）动作，比水平钢琴需求更少的空间。铸铁板支撑弦力，高张力限的钢琴丝容许直径更粗张力更大的琴弦，提高了声音能量和亮度。压缩毡代替了皮革榔头覆盖物，柔化了音色并且提高了榔头的控制力和耐久力。将低音弦与高音弦交叉减小了钢琴尺寸，更多斜交叉的琴弦和间击动作（drop action）导致更小的立式钢琴。

一音多弦对钢琴独特的音色具有重大意义，因为琴弦校准中的细微差异给每个音色增加了合唱效果。研究表明，相对数学上完全校准而言，听觉更喜欢轻微去谐（小于0.1%）的同度琴弦；有经验的钢琴调音师专门保留这一校音幅差。在榔头敲击琴弦后的那一刻，多根琴弦近似同步地颤动。这时，传送到弦马和音板的声音能量比例最大，导致音色的起始衰减速度很快。随后，琴弦因其频率的细微差异渐渐变成非同步，音符衰减的速度更慢一些。这种良好调律的钢琴中的双衰减特性，使后继音符在当前演奏的保持音符上突显出来，并且影响了钢琴作曲的发展。当延音踏板升起止音器时，被敲击琴弦的颤动通过钢琴弦马传给其他琴弦共振，产生更强的合唱效果。在三角钢琴中，弱音踏板将动作横移，减少榔头敲击琴弦的数量。

除了最高音，每个钢琴音符包含很多分音，主要集中于100 Hz ～ 1 000 Hz之间。遍布整个音高范围的榔头击弦声是钢琴音色的重要特征，但仅在最高音区被注意到，那里分音过于稀疏，掩盖不了它。

钢琴调音师们调校八度所采用的标准程序制造出一个延展音阶。高音更高，低音更低，两端比严格的十二平均律多三分之一个半音，结果是琴弦音色分音的轻微不谐和。研究表明钢琴家及听众喜欢这种音阶延展的方式，而且以严格泛音列分音合成真钢琴音色的尝试不得不受成效的限制。

科学、工程学与艺术在钢琴构成的演变中组合起来，被认为是与音色相关的主要构件配制方案的“品级设计（scale design）”。这些包括琴弦、榔头、止音器、弦马、音板、钢板以及一些外延，外壳连同它们材质的属性。

注：本文根据《格罗夫音乐辞典》中声学词条部分的内容编译而成。

参考书目

［1］F.Trendelenburg, E.Thienhaus and E.Franz: ‘Zur Klangwirkung von Klavichord, Cembalo und Flügel’,Akustische Zeitschrift, v (1940), 309

［2］D.Martin: ‘Decay Rates of Piano Tones’, JASA,xix (1947), 535–41

［3］R.E.Kirk: ‘Tuning Preferences for Piano Unison Groups’, JASA, xxxi (1959), 1644–8

［4］D.Martin and W.D.Ward: ‘Subjective Evaluation of Musical Scale Temperament in Pianos’, JASA, xxxiii(1961), 582–5

［5］D.Droysen: ‘Akustische Untersuchungen an Tasteninstrumenten des 18.–20.Jahrhunderts’, GfMKB:Leipzig 1966, 416–23

［6］S.Tomek-Schumann: ‘Akustische Untersuchungen an Hammerfl ügeln’, JbSIM (1975), 127–72

［7］R.-D.Weyer: ‘Time-Varying Amplitude-Frequency-Structures in the Attack Transients of Piano and Harpsichord Sounds’, Acustica, xxxv (1976), 232–52;xxxvi (1976), 241–58

［8］E.L.Kent, ed.: Musical Acoustics: Piano and Wind Instruments (Stroudsburg, PA, 1977)

［9］V.G.Porvienkov, M.V.Gridněv and N.elnokov:‘Hodnocení hlasitosti a barvy zvuku klávesového nástroje’ [Measuring the volume and colour of the sound of keyboard instruments], Hudební nástroje, xv/1 (1978),14–17

［10］U.R.Müller: ‘Infl uence of Ribs on the Acoustic Behaviour of Piano Resonant Plates’, Archives of Acoustics, v (1980), 147–55

［11］K.Wogram: ‘Die Bedeutung nichtstationärer Schwingungsvorgänge für die Bewertung von Musikinstrumenten’, Qualitätsaspekte bei Musikinstrumenten, ed.J.Meyer (Celle, 1988), 23–34

［12］J.Meyer and K.Wogram: ‘Perspektiven der Musikinstrumentenakustik’, Acustica, lxix (1989), 1–12

［13］M.Podlesak and A.R.Lee: ‘Effect of Inharmonicity on the Aural Perception of Initial Transients in Low Bass Tones’, Acustica, lxviii (1989), 61–6

［14］A.Askenfelt, ed.: Five Lectures on the Acoustics of the Piano (Stockholm, 1990)

［15］A.Askenfelt and E.Jansson: ‘From Touch to String Vibrations’, JASA, lxxxviii (1990), 52–62; xc(1991), 2383–93

［16］A.I.de La Campa: Aproximación analítica a la interpretación en el piano (Madrid, 1990)

［17］H.Suzuki and I.Nakamura: ‘Acoustics of Pianos’, Applied Acoustics, no.30 (1990), 147–205

［18］X.Boutillon: Aperçu général sur les modèles physiques de piano (Paris, 1991)

［19］A.Chaigne and A.Askenfelt: ‘Numerical Simulations of Piano Strings’ JASA, xcv (1994), 1112–18, 1631–40

［20］I.Bork, H.Marshall and J.Meyer: ‘On the Radiation of Impact Noises from a Grand Piano’,Acustica, lxxxi (1995), 300–08

［21］H.Conklin: ‘Design and Tone in the Mechanoacoustic Piano’, JASA, xcix (1996), 3268–96; c(1996), 695–708, 1286–98