滚动轴承故障诊断的改进小波变换谱峭度法

沈金伟，石林锁

(第二炮兵工程学院 五系，西安 710025)

采用传统的包络分析方法进行故障诊断，结果与操作者的经验或掌握的历史数据紧密相关。因此文献[1]提出了基于谱峭度的改进包络分析法，此方法有效地实现了符合最佳包络的频带的自动检测，并在实际工作中得到了检验，但是其只研究了一组Morlet复小波滤波器组，没有深入研究多组滤波器组比较下的最优结果。文献[2]对其进行了改进，设计了多组Morlet复小波滤波器组，每一组的滤波器数目不同，将这些滤波器组应用到故障检测中，选出最大谱峭度对应的最优Morlet复小波滤波器，利用此滤波器对原始信号的滤波结果，得到包络分析结果，最终检测故障频率。需要指出的是由此法得到的最大谱峭度是出现在每倍频程六个滤波器的条件下，比文献[1]采用的五个滤波器的情况结果更优。

虽然文献[1-2]都采用了小波变换谱峭度法寻找最大谱峭度，进而找到对应的最佳Morlet复小波滤波器及其滤波信号，并且取得了理想结果，然而此方法是在人为选取多组Morlet复小波滤波器的基础上进行的，要真正找到最优滤波器仍需在此基础上再比较更多组滤波器组，过程很繁琐。考虑到谱峭度与构造最优匹配滤波器之间有着密切的关系[3-4]，在总结前人研究的基础上，将谱峭度构造最优滤波器的特性与基于Morlet小波分解求谱峭度的方法结合起来，并由此取得了比原方法更加优良的检测和诊断性能。

1 谱峭度与改进小波谱峭度法的实现

1.1 谱峭度与基于谱峭度的最优匹配滤波器

不同的小波函数具有不同的时频结构，考虑到故障轴承所产生的暂态冲击振动响应成分，可以发现Morlet复小波能够最好逼近此类尖锐变化的信号，因此一般选用Morlet复小波对原始信号进行小波变换[1]。

为了最大限度地发挥Morlet复小波作为一个滤波器组的特点，同时为了使信号的时域和频域表示能得到很好对应，就有必要设计多个滤波器组，且每个滤波器组的每倍频程上的滤波器数目应不相同[2]。

谱峭度是在峭度的概念上发展起来的一个时频域检测指标，应用于机械故障诊断的基本原理是将故障信号经过时频分解得到其时频域分布，而后在每一个频带上计算信号的时域峭度，因此其对暂态冲击成分十分敏感，通过分析不同频带上的峭度值即可指示出故障的存在，实现早期故障诊断。文献[3-4]对其有一个比较详细和系统的定义：

(1)

式中：C4Y(f)为过程Y(t)的4阶谱累计量；S(f)为谱瞬时矩。根据此方法定义的谱峭度具有很多重要的性质[3]，在此需要用到的性质是：对于一个CNS过程z(t)=y(t)+n(t)(其中n(t)是与信号y(t)相互独立且平稳的高斯噪声信号)，则其谱峭度为:

(2)

式中：ρ(f)=S2N(f)/S2Y(f),代表信噪比，是频率的函数。值得指出的是，在ρ(f)很大的地方过程的谱峭度值接近于0，而在ρ(f)很小的地方其值近似等于KY(f)，因此通过搜索整个频域，可以找到谱峭度最大的频带，即为故障频带，这也表明了谱峭度对与检测故障的优越性。由(2)式发现了谱峭度与最优匹配滤波器设计之间的关系，即:

(3)

将(2)式代入(3)式得：

(4)

式中：k为未知参数，其获取可以先假设一个比较小的值代入(4)式，构造最优匹配滤波器，而后通过多次迭代找到使滤波器滤波后相应输出信号的峭度值最大的k值，从而确定参数k。应用此滤波器可以使y(t)*m(t)与n(t)*m(t)功率比达到最大，即实现信噪比最大化。根据暂态波形是确定的还是随机的，相应的有两种构造方法[4]:

(1)波形确定的情况下，可直接通过(4)式进行构造。

(2)波形随机的情况下，利用(4)式的逆Fourier变换组成一自相关阵，通过求自相关阵给出的最大特征值所对应的特征向量，去构造相应的最优匹配滤波器。

事实上，一般都认为波形是随机的，所以都按(2)的情况构造。

基于滤波器对谱峭度的依赖，必须首先选用时频分解得到谱峭度值，考虑到Morlet复小波在已有小波函数中最逼近轴承振动冲击信号[1]，因此选用了基于Morlet复小波的小波变换，但Morlet复小波是事先人为确定的，相比之下根据谱峭度构造的最优匹配滤波器则应该更具有灵活性和匹配特性。为了验证此结论，在原有小波变换谱峭度法的基础上做了相应改进。

1.2 改进小波谱峭度法的实现

(1)设计Morlet复小波滤波器组，相关参数如下[2]：

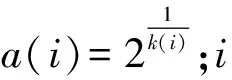
②Q=2/k(i)；使每个滤波器的带宽等于各个滤波器之间的间隔。

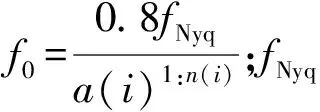
④带宽σ=Q×f0；一旦这些参数得到确定，就可以生成需要的滤波器组。

(2)将原始信号的FFT与滤波器组矩阵的每一行相乘，然后对结果进行IFFT运算得到小波系数。

(3)将小波系数与其复共轭做乘积得到滤波后信号的时域平方包络。

(4)根据(1)式定义计算相应的谱峭度值。

(5)利用求得的谱峭度值，根据上述方法构造匹配滤波器，对此原始信号进行滤波，并作平方包络分析，得到其包络谱，进行故障识别和诊断。

2 改进小波变换谱峭度法在仿真信号中的应用

本文采用文献[5]的故障仿真信号，用一个单自由度弹簧-质量-阻尼振动系统模拟轴承局部故障产生的振动冲击，并在冲击的时间间隔上引入了微小的随机变化，以更好逼近实际信号。其故障特征频率为200 Hz，共振频率为9 000 Hz，采样频率为32 768 Hz。下面利用该仿真信号来对比检验强噪声背景下小波变换谱峭度法与改进小波变换谱峭度法的检测性能。

图1和图2显示对混入能量为32 dB的高斯白噪声的仿真信号应用小波变换谱峭度法和改进小波变换谱峭度法后得到的平方包络谱图，可以看到，当噪声干扰不是很大的时候两者的检测效果基本一致，都能精确检测出200 Hz的故障频率。

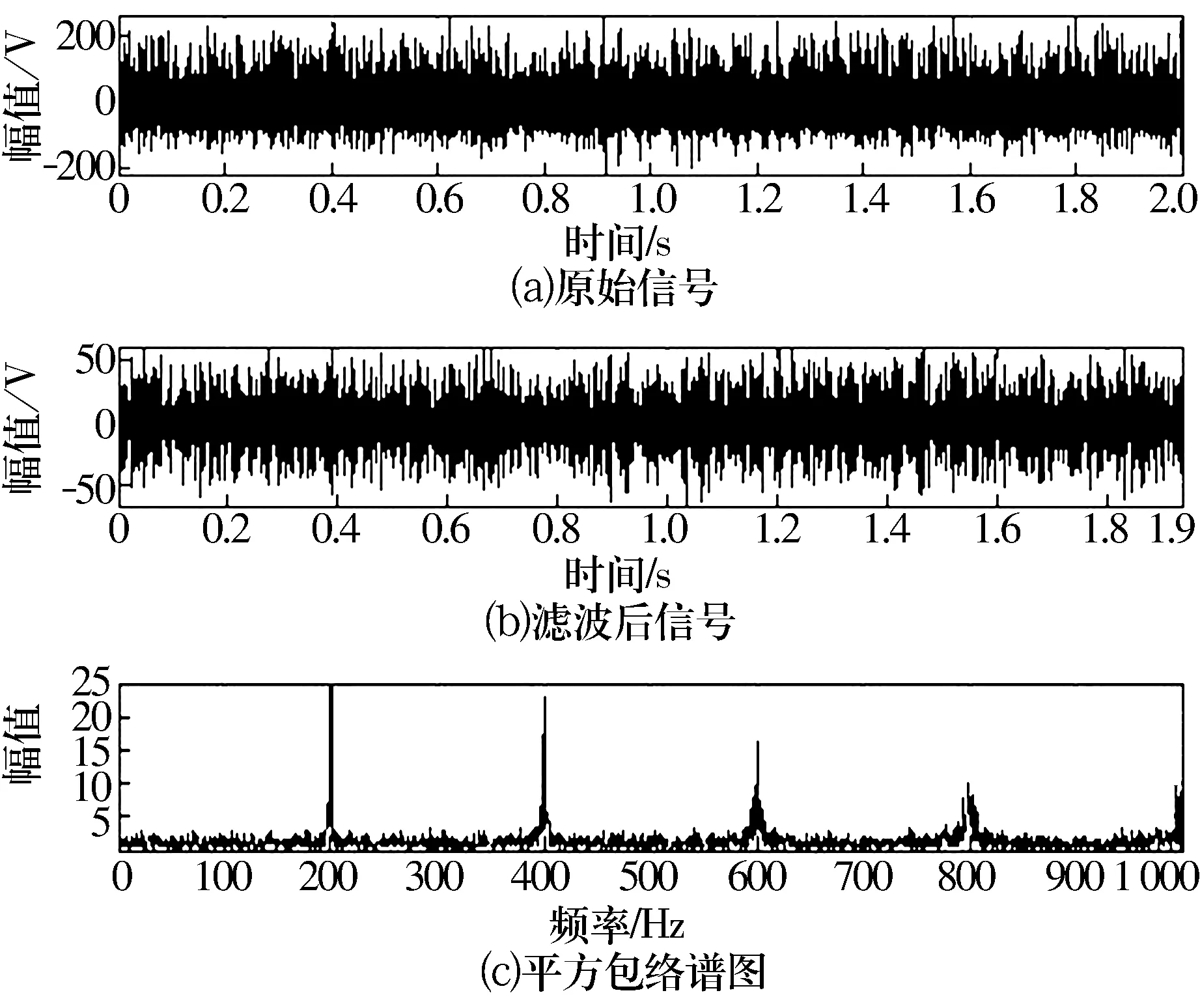
图1 基于Morlet小波滤波的小波变换谱峭度法结果

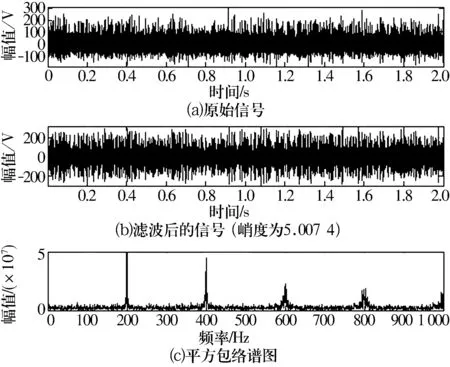
图2 使用匹配滤波器滤波后的小波变换谱峭度法结果

为了更好地比较两者的有效性，将噪声能量提高到40 dB，该条件下最优匹配滤波器见图3。试验结果见图4和图5，由图可知，基于Morlet小波滤波的小波变换谱峭度法已经无法检测出故障(事实上研究结果表明当有能量高于35 dB的噪声干扰时此方法已基本失效)，而改进的小波变换谱峭度法仍能很好地检测出200 Hz的故障频率，而且还能适应噪声能量更高的噪声环境。

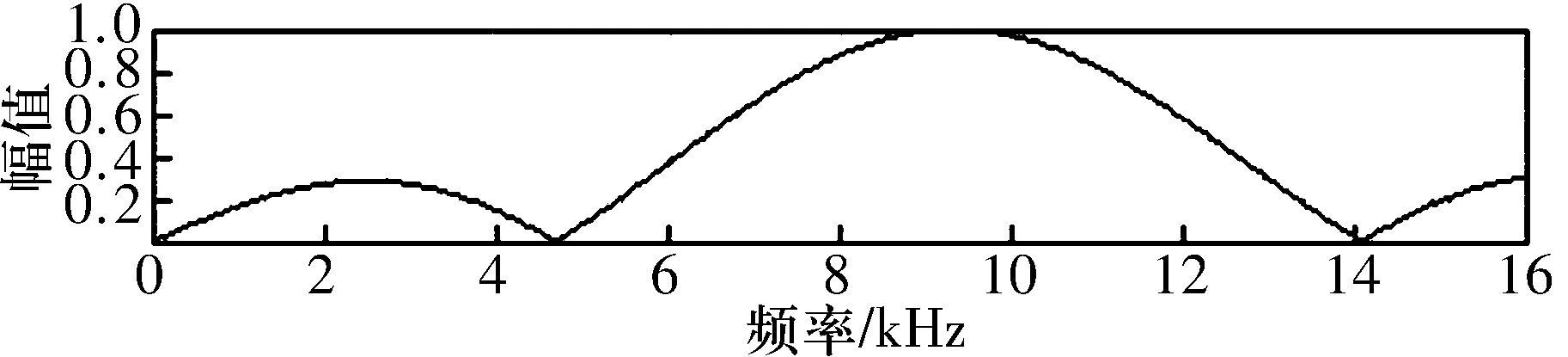
图3 混入能量为40 dB的噪声条件下的最优匹配滤波器

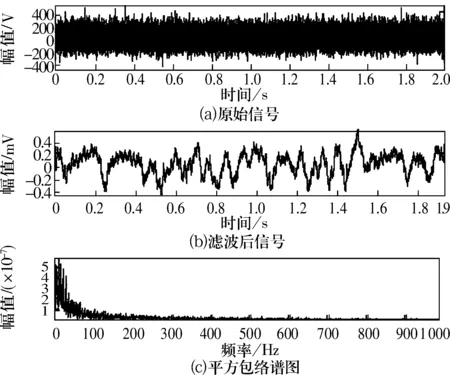
图4 基于Morlet小波滤波的小波变换谱峭度法结果

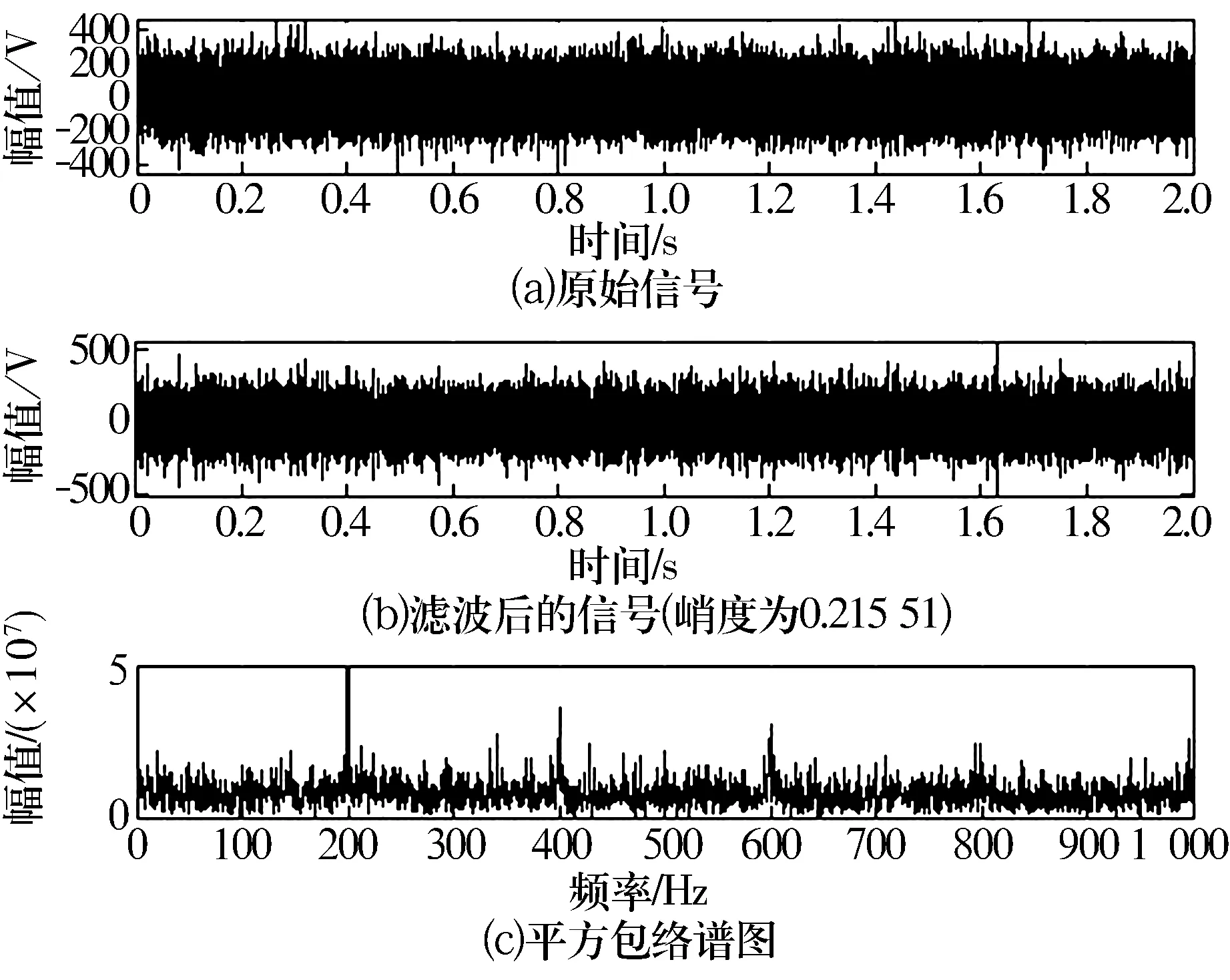
图5 使用匹配滤波器滤波后的小波变换谱峭度法结果

由以上比较分析可知，强噪声背景下，改进的小波变换谱峭度法具有更强的适应能力和检测效果。

3 改进小波变换谱峭度法在实测信号中的应用

实际信号采自安装在一个变速箱中存在内圈点蚀故障的滚动轴承，变速箱轴的转速fr=10 Hz，钢球个数Z=12，钢球直径Dw=7.12 mm，球组节圆直径Dpw=38.5 mm，接触角φ=0，采样频率为4.8 kHz。根据平稳工况条件下轴承内圈故障特征频率计算公式可知其内圈故障频率为71.1 Hz。下面用改进方法来检测此故障。

首先计算其谱峭度值，并构造匹配滤波器。图6、图7分别为快速谱峭度图[6]和构造的匹配滤波器单边谱图。

图6中纵坐标表示每倍频程上的滤波器个数，Kmax为最大谱峭度值，fc为得到最大值时的滤波器中心频率。将如图7所示构造的匹配滤波器应用到实际信号中，其检测效果如图8所示，与仿真信号的试验效果一致，精确地检测出了内圈故障特征频率71.1 Hz。

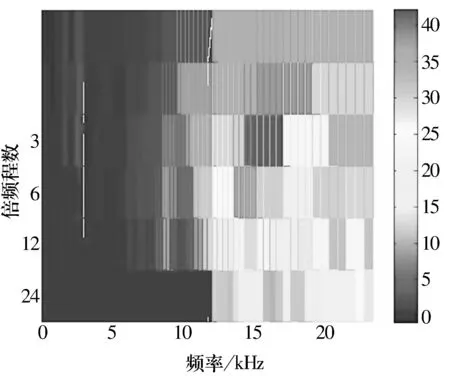
图6 小波变换谱峭度图

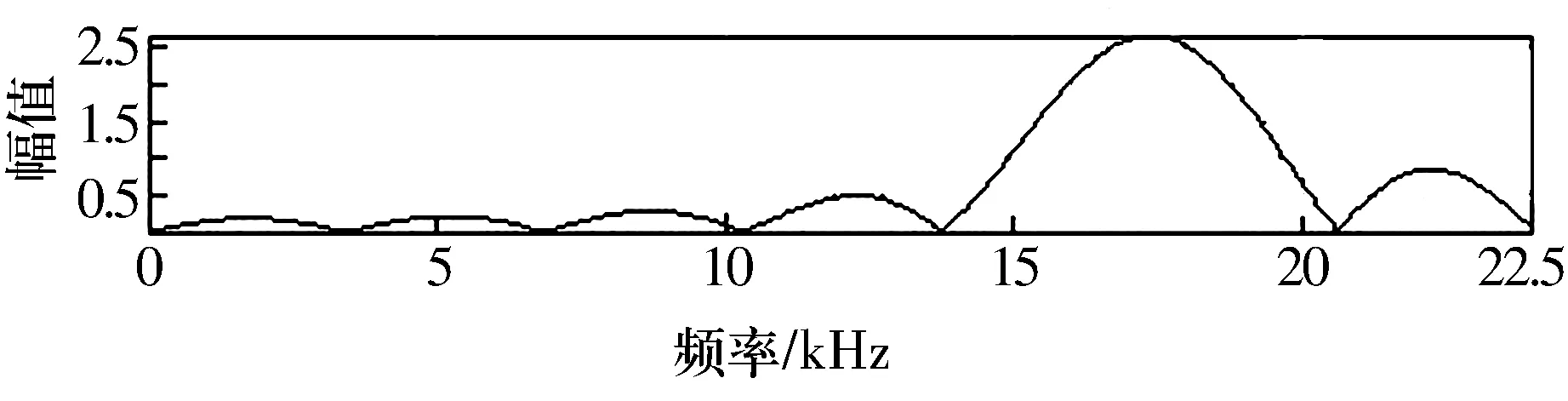
图7 改进小波谱峭度法构造的滤波器

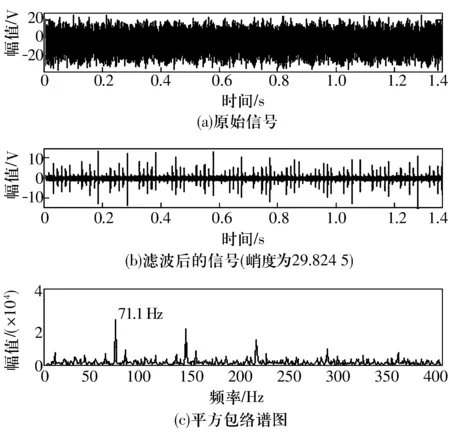
图8 改进小波变换谱峭度法实测结果

4 结束语

在结合前人研究成果的基础上，利用谱峭度与构造匹配滤波器之间的重要关系，对小波变换谱峭度法进行了改进。相对于Morlet小波滤波器的事先人为设计的特点，由于用谱峭度构造的匹配滤波器具有更好的自适应性和匹配特性，因此应用此匹配滤波器应该具有更强的实用性，且给出了相应的仿真效果比较，结果证明了此结论。最后将此方法应用到实测信号中，同样取得了理想的效果。