一种磁性齿轮传动装置

杜世勤 江建中 章跃进 龚 宇

（上海大学机电工程与自动化学院 上海 200072）

1 引言

磁性齿轮传动装置利用磁力传动，无机械接触，克服了机械齿轮传动装置所固有的机械疲劳、摩擦损耗、振动噪声等缺点；运行过程中无需润滑，清洁、无油污；在过载时可及时隔断传动关系，具有自保护功能。所以，磁性齿轮传动装置的研究为传动产业提供了一个新的发展方向。

磁性齿轮传动装置的概念最早见于20世纪初，1913年美国就有人申请了关于磁性齿轮传动装置的专利[1]，但是一直没有引起人们的太多关注。这一方面是由于过去永磁材料的磁性能较差，导致磁性齿轮传动装置的转矩密度无法提高，限制了磁性齿轮传动装置的应用，另外一个更重要的原因是受传统磁性齿轮传动装置拓扑结构限制，永磁体利用率很低，如图1所示。

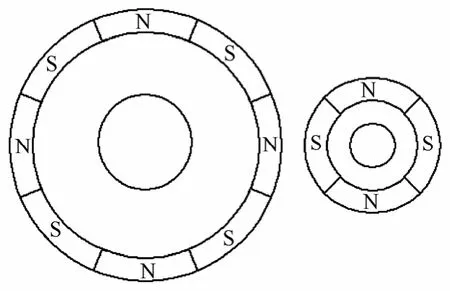
图1 传统磁性齿轮传动装置Fig.1 Conventional magnetic gearing

2001年，英国Sheffield大学的学者K.Atallah and D. Howe提出了一种新结构磁性齿轮传动装置—磁场调制式磁性齿轮传动装置[2]，如图 2所示，克服了传统磁性齿轮传动装置转矩小的缺点。在此基础之上，国内外学者集思广益，开发了各种磁路结构和不同场合使用的磁场调制式磁性齿轮传动装置[1,3-6]。

图2 磁场调制式磁性齿轮传动装置Fig.2 Magnetic field modulation gearing

研究表明，永磁无刷电机在自然冷却、强制风冷和水冷却的条件下，其转矩密度可分别达到10kN·m/m3、20kN·m/m3、30kN·m/m3，横向磁通永磁电机的转矩密度可达40～60kN·m/m3[7]，而磁场调制式磁性齿轮传动装置转矩密度可达72kN·m/m3[7]。磁场调制式磁性齿轮传动装置研究取得的重大进展为高转矩密度电机的研制提供了新的途径。

2 磁场调制式磁性齿轮传动装置的工作原理

本文提出了这种新型磁性齿轮传动装置对应的一种实现结构（见图 3）。在该实例中，包括外转子、内转子，两者之间为调磁环。内、外转子均采用表面式磁钢，高速的内转子是4对极，低速的外转子是17对极，调磁环为开直通槽铁心，齿数21。内外转子、调磁环铁心均为硅钢片叠压构成，表 1列出了此磁性齿轮传动装置的设计参数。

图3 磁场调制式磁性齿轮传动装置结构图Fig.3 Magnetic field modulation gearing structure

表1 磁性齿轮传动装置的设计参数Tab.1 Parameters for the magnetic field modulation gearing

这种磁场调制式磁性齿轮传动装置工作的基本原理在于使用了导致气隙磁导变化的调磁环，调制了两边转子上永磁体产生的磁场，使调制好的磁场具有的谐波与对面转子上的永磁体相互作用。

不管哪个转子永磁体产生的磁场，可以得出其空间谐波磁通密度分布的极对数如下[7]

式中p——转子的极对数；

ns——调磁铁心的块数。

而磁通密度空间谐波的旋转速度为

式中Ωr——其中任一个转子的旋转速度；

Ωs——调磁环的旋转速度。

从式（1）、式（2）可以分析磁通密度的空间谐波分布和旋转速度，进而得出磁性齿轮传动装置的速比，作为磁性齿轮传动装置的设计的理论基础，下面进行具体的分析。

在本设计中内转子极对数p=4，外转子极对数p＝17，调磁环块数ns=21。根据式（1），当p=4时，主要的谐波有p1,0=4次，p1,-1=17次；当p=17时，主要的谐波有p1,0=17次，p1,-1=4次。由式（2）可以看出，由于调磁铁心环的引入，即k≠0，经过调磁环调制的气隙磁通密度空间谐波的旋转速度，是不同于永磁体所在的转子的转动速度的。这样的话，要在不同的转速下传递转矩，另一个永磁体转子的极对数就必须等于k≠0时的一个空间谐波的极对数。正如上面所分析的，4对极的转子磁体磁场调制后的一个空间谐波的极对数为17，正好等于另一个转子上的极对数。反之亦然。因为m=1，k=-1的组合，可以产生除基波之外的幅值最大的空间谐波，那么另一个转子的极对数就必须等于（ns-p）。进而就可以给出这种磁性齿轮的速比，当Ωs=0，亦即铁磁材料的调磁环静止不动时，有

3 数值解析结合法磁场计算

从工作原理的分析过程中，可以得出这样的一个结论：调制磁场磁通密度谐波的分析是这种新型磁性齿轮传动装置设计时最为重要的一个环节。理论分析是定性的一个方面，对于磁性齿轮传动装置复杂的磁路而言，重要的是拿出定量的谐波分布数值。

本文采用数值解析结合法[8-9]计算具有两层气隙的磁性齿轮传动装置。如果用纯有限元法计算，要实现两个转子以不同转速、不同转向的转动将十分困难。其根本原因是气隙网格的存在，使得定转子之间产生了硬性连接。数值解析结合法将气隙磁场用解析法表示，气隙区域无网格，转子可以自由转动。

将两层气隙的磁性齿轮传动装置求解区域划分为定子、转子和气隙三类，几何形状复杂、含有非线性媒质的区域归入定子或转子区域，用有限元法处理。气隙区域形状规则，可以获得磁场解析表达式。三类区域的磁场根据场域的交界条件建立联系，各区域相互联系又相对独立，每个区域只要建立起描述区域内部磁场的数学模型既可。为了区分两层气隙，程序中需对每层气隙对应的气隙边界节点给出标识。在极坐标下气隙磁场矢量磁位Az的解析表达式为

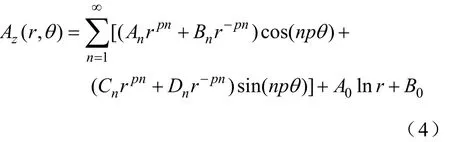
式中，An、Bn、Cn、Dn、A0、B0是傅里叶系数；r，θ是气隙内各点的极坐标；p为周期数，其引入是基于磁场周期性区域的考虑。实际过程中，磁性齿轮传动装置定转子区域通过有限元法离散剖分，形成系数矩阵。但尚未包括气隙部分的场量，气隙表面的节点没有发生联系，矩阵还不完整。根据气隙区域磁场解析表达式，可以求得气隙能量泛函的偏导数，从而获得同层气隙表面节点相关的系数。将相关系数“贡献”到矩阵的对应元素中，最终形成整个区域的总体方程式。

数值解析结合法除了能够实现转子自由转动以外，计算结果中包括气隙区域内、外边界的磁位，气隙磁通密度的级数形式的解析表达式为[9]

式中，Rr、Rs是气隙的内、外半径；an、bn是气隙外边界磁位函数对应的傅里叶系数；cn、dn是气隙内边界磁位函数对应的傅里叶系数。an、bn、cn、dn和An、Bn、Cn、Dn的关系表达式参见文献[10]。由式（5）可以直接进行磁性齿轮传动装置的气隙磁通密度谐波的定性和定量分析。根据麦克斯韦应力张量法理论，由气隙磁通密度可以导出电磁转矩的解析表达式[9]

式中，对于选定的半径，r为常数，当然电磁转矩的计算结果与积分半径无关，这样就摆脱了纯有限元法转矩计算精度受到气隙网格影响的困扰。

结合设计，给出这一新型磁性齿轮传动装置的数值解析结合法的计算结果。

传动力矩是永磁齿轮传动机构最重要的性能指标之一，准确计算永磁齿轮传动机构的传动力矩，是分析、设计永磁齿轮传动机构的关键。以下是外转子旋转360°电角度，其间间隔为6°电角度，而定子和内转子保持不动得到的转矩计算结果，如图4所示。从图中可以看出外转子转到90°电角度时，该永磁齿轮传动机构取得最大转矩，此时该磁性齿轮磁力线的分布如图5所示。

图4 矩角特性Fig.4 Torque versus angle

图5 磁力线的分布Fig.5 Calculated flux lines

下面具体分析在该位置处内外层气隙的磁场分布和相应的转矩传递。

有关内外转子永磁体单独励磁时，磁场被调磁环调制的情况和对应的谐波分析，参见文献[2]。

根据式（5）计算，外层气隙中间的径向磁通密度分布如图6所示，这是内外转子永磁体作用的合成磁场，经过调制，增加了谐波成分。不难看出，靠近 17对极外转子的气隙合成磁场，17对极的径向分量占主要部分，4对极的内转子的磁场分量，叠加在17对极的主波之上。进一步计算可得外层气隙中间径向磁通密度的空间谐波分量如图7所示。显而易见，这是一个含有较多谐波成分的合成磁场。参与转矩传递的主波及其贡献大小是我们所关心的一个重要方面。外层气隙里，根据式（6）计算得到的转矩谐波分析如图8所示，从图8中可以看出只有主波转矩一项，其余的谐波转矩忽略不计。同理可得内层气隙中间径向磁通密度如图9所示，内层气隙中间径向磁通密度对应的空间谐波分析和内层气隙里转矩谐波分析如图 10、图 11所示。比较内外层气隙中电磁转矩的主波成分，其比值是4∶17，仿真计算得到的结果与前面理论分析相一致。

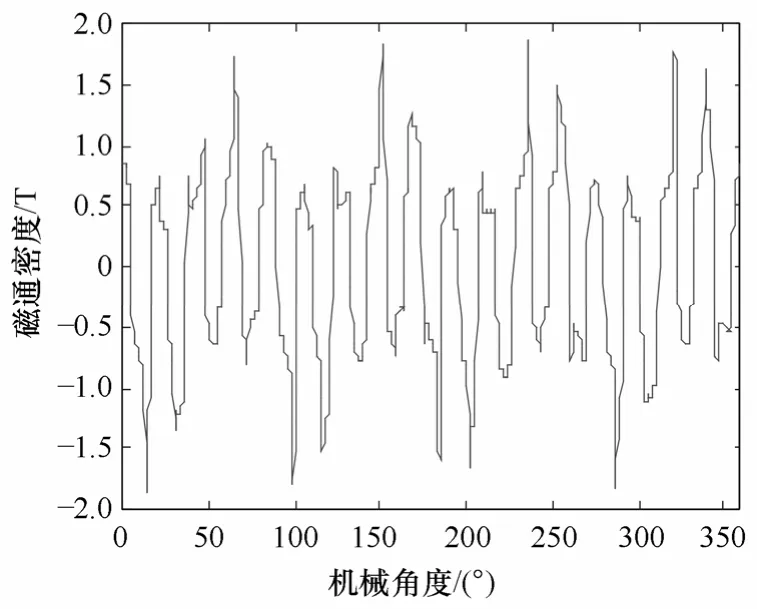
图6 外层气隙中间径向磁通密度Fig.6 Radial flux density in middle outer airgap

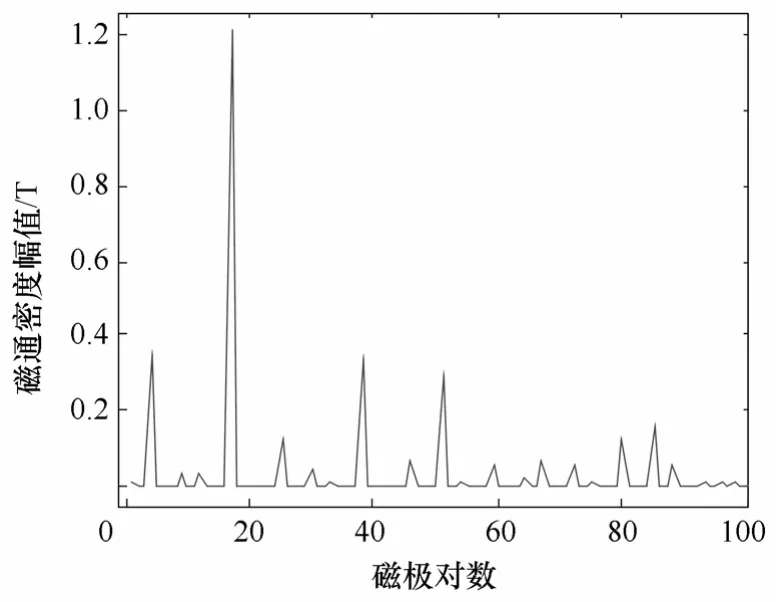
图7 外层气隙中间径向磁通密度对应的空间谐波分析Fig.7 Harmonics of radial flux density in middle outer airgap

图8 外层气隙的转矩谐波Fig.8 Harmonics of torque in the outer air gap

图9 内层气隙中间径向磁通密度Fig.9 Radial flux density in middle inner air gap

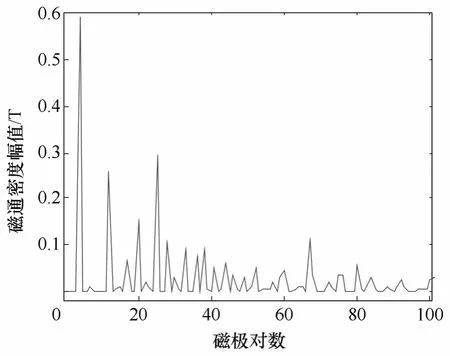
图10 内层气隙中间径向磁通密度对应空间谐波Fig.10 Harmonics of radial flux density in middle inner air gap

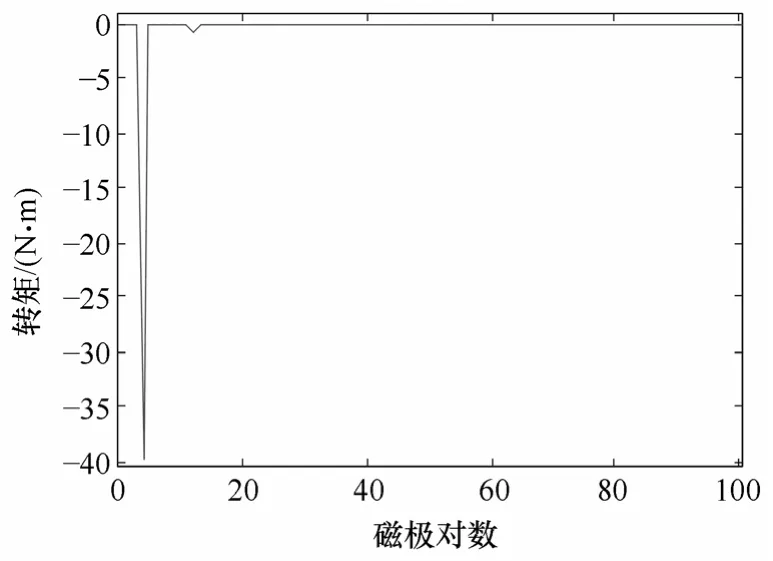
图11 内层气隙的转矩谐波Fig.11 Harmonics of torque in the inner air gap

4 样机和试验

采用图2和图3的结构及表1的参数，设计、加工了一台磁性齿轮传动装置的样机，图12、图13分别为样机照片和试验平台。

图12 样机照片Fig.12 Photograph of the constructed gearing

图13 试验平台Fig.13 View of experimental setup

经过空载和带载试验，发现磁性齿轮传动装置能不失步地起动。在同一负载转矩下调速，以及在同一转速下调负载转矩，都能稳定、平滑地运行，而且噪声不大。

空载实验结果如图14所示。图中可见空载损耗随着转速的升高而增大，原因是磁性齿轮传动装置中的铁损耗、机械摩擦损耗以及风摩损耗都与转速有关，特别是铁损耗随着转速的升高变化较大。将空载损耗与外转子转速的关系用指数公式进行拟合，得到指数系数是1.6。

表 2、表 3给出外转子负载侧转速分别为50r/min和 150r/min时的负载实验结果。从负载实验结果看，磁性齿轮传动装置传递效率与其负载的大小有着很大的关系，这是由于磁性齿轮传动装置的负载损耗和空载损耗基本一致，因此负载轻时齿轮传动装置效率较低。就样机来讲，低速外传子在50～150r/min速度范围内，当负载转矩等于80N·m时，其传递效率在90%以上。

在负载转矩达到80N·m时，样机的有效长度对应的输出转矩密度达到56kN·m/m3。

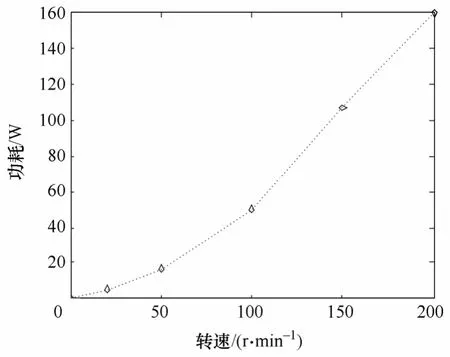
图14 空载损耗曲线Fig.14 Curve of power losses with no load

表2 负载侧转速为50r/min时的效率Tab.2 Results of efficiency when output speed is 50r/min

表3 负载侧转速为150r/min时的效率Tab.3 Results of efficiency when output speed is 150r/min

5 结论

磁场调制式磁性齿轮传动装置，内、外层气隙之中磁场有多种谐波分量存在，但是电磁转矩几乎是单一主波成分，实验证明样机在不同转速和不同负载转矩的情况下能稳定运行。对于求解区域里面有多个气隙的情况，数值解析结合法分析在计算程序里给予不同的标识，根据磁位计算结果，得到各气隙的磁通密度分布和电磁转矩的解析表达式，电机有限元软件实现了从单气隙到多气隙的拓展应用。样机取得了 56kN·m/m3的高转矩密度、93%以上的高传动效率的结果。

[1] Peter Omand Rasmussen, Torben Ole Andersen, Frank T Jørgensen, et al. Development of a high-performance magnetic gear[J]. IEEE Transactions on Industry Applications, 2005, 41(3): 764-770.

[2] Atallah K, Howe D. A novel high-performance magnetic gear[J]. IEEE Transactions on Magnetics,2001, 37(4): 2844-2846.

[3] Atallah K, Wang J, Howe D. A high-performance linear magnetic gear[J]. Journal of Applied Physics,2005, 97(10): 10N516.1-10N516.3.

[4] Mezani S, Atallah K, Howe D. A high-performance axial-field magnetic gear[J]. Journal of Applied Physics, 2006, 99(8): 08R303.1-08R303.3.

[5] Li Yong, Xing Jingwei, Peng Kerong, et al. Principle and simulation analysis of a novel structure magnetic gear[C]. International Conference on Electrical Machines and Systems, 2008: 3845-3849.

[6] Nicolas W Frank, Hamid A Toliyat. Gearing ratios of a magnetic gear for marine applications[C]. 2009 IEEE Electric Ship Technologies Symposium, 2009:477-481.

[7] Atallah K, Calverley S D, Howe D. Design, analysis and realisation of a high performance magnetic gear[J]. IEE Proc. Electr. Power Appl., 2004, 151(2):135-143.

[8] 章跃进, 江建中, 屠关镇. 应用数值解析结合法计算旋转电机磁场[J]. 电工技术学报, 2004, 19(1):7-11.

Zhang Yuejin, Jiang Jianzhong, Tu Guanzhen.Application of numerical-analytical method to magnetic field computation in rotating electric machines[J]. Transactions of China Electrotechnical Society, 2004, 19(1): 7-11.

[9] 章跃进, 江建中, 崔巍. 数值解析结合法提高电机磁场后处理计算精度[J]. 中国电机工程学报, 2007,27(3): 68-72.

Zhang Yuejin, Jiang Jianzhong, Cui Wei. Accuracy enhancement of post process of magnetic field computation for rotational electric machines by numerical-analytical method[J]. Proceedings of the CSEE, 2007, 27(3): 68-72.

[10] 章跃进. 旋转电机磁场计算数值解析结合法研究[D]. 上海: 上海大学, 2005.