粒子滤波在轴承故障振动信号降噪中的应用

刘晓平，郑海起，张训敏

（1.军械工程学院，石家庄 050003；2.济南军区72465部队，济南 250022）

滚动轴承产生早期故障时，故障信号比较微弱，往往被湮没在强大的背景噪声中。如何把微弱的有用信号同噪声分开，提高信号的信噪比，为故障特征频率的提取提供可靠的依据，成为轴承故障诊断中的重要问题之一。

小波及小波包滤波在机械故障诊断的信号预处理中有着广泛的应用［1-2］。但这类滤波方法没有充分利用信号自身的特性。Kalman滤波给出的是线性Gauss系统的最优滤波，而在机械故障诊断中，存在着大量的非Gauss的噪声且要求实时处理，粒子滤波则是研究非线性、非Gauss动态系统最优估计问题的一个很有效的实时处理方法。

1 振动信号的状态空间模型

对于一般机械故障的振动信号，由于故障形式的多样性和故障机理的复杂性，通过分析机械故障产生的机理，建立产生信号的准确模型很困难。因此根据待处理数据本身的特点，利用现代时间序列分析方法建立振动信号的模型。设原始信号为xt，其时变自回归模型为：

式中：at＝（a1，t，a2，t，…，ak，t），其为时变自回归模型的系数；σet为模型激励信号的方差，且et～N（0，1）。

假设原始信号湮没在背景噪声中，实测信号与原始信号的关系可表示为：

定义：Xt＝（xt，xt-1，…，xt-k+1），

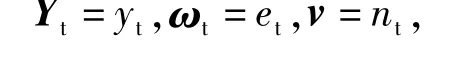
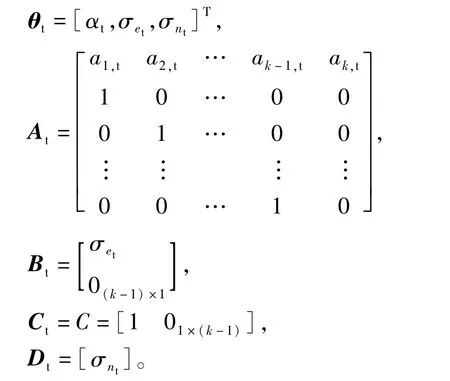
振动信号的状态空间模型可表示为：

在实际中只能测得一个被噪声污染的信号Yt，通过建立上述的状态空间模型，利用粒子滤波实现对参数θt和Xt的估计，从而实现信号的降噪。

2 粒子滤波

粒子滤波［3-5］是一种基于Monte-carlo方法的Bayes滤波算法。粒子滤波通过非参数化的Monte-carlo模拟方法来实现递推Bayes滤波，适用于任何能用状态空间模型表示的非线性系统。

2.1 MCMC方法

重采样思想能解决粒子滤波中的粒子退化问题，但却导致粒子多样性的丧失，使描述状态后验概率密度的粒子不够充分。MCMC方法是粒子滤波中增加粒子多样性的一个重要方法，常用的采样方法有Gibbs采样和Metropolis-Hasting方法。这里采用Metropolis-Hasting方法，需交替迭代以下两步：

2.2 Rao-blackwellised粒子滤波（RBPF）［6-7］

粒子滤波可以递归的产生一组加权粒子来逼近后验概率p（χt｜y1∶t），在维数很高的状态空间采样时，PF的计算量大，效率很低，限制了粒子滤波在实际中的应用。对某些状态空间模型，状态向量的一部分在另一部分的条件下的后验分布可以用解析方法求得，例如某些状态在另一部分的条件下是线性Gauss模型，可用Kalman滤波器得到条件后验分布，对另外部分状态用PF，从而得到一种混合滤波器——RBPF，其降低了PF采样空间的维数。RBPF样本的重要性权的方差远远低于SIR方法的权的方差。假设χt可以表示为［χt，θt］，如果给定θt，Xt退化为线性Gauss状态空间系统，就可以用Kalman滤波器进行估计。即根据Bayes准则，后验概率密度可以分解为：

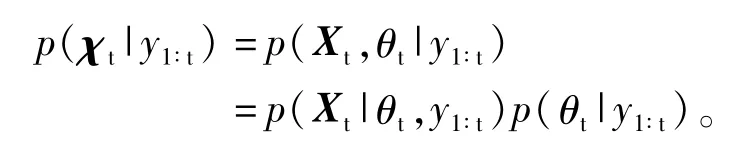
如果知道边缘后验概率p（θt｜y1∶t），p（Xt｜θt，y1∶t）是Gauss分布的，并且可以求出解析解。总之，RBPF跟粒子滤波相似，不同的是其只对θt进行采样，每次采样后用Kalman滤波器更新Xt的均值和方差，在参数估计［8］、动态Bayes网络［9］、语音信号处理［10-12］中都有着成功的应用。

2.3 基于RBPF的振动信号降噪算法步骤

⑤粒子滤波量测更新（重采样过程）。当j＝1，2，…，N，从｛θk｜k-1（j），μk｜k-1（j），∑k｜k-1（j）｝中重采样N次获得N个粒子组｛θk（i），μk｜k-1（i），∑k｜k-1（i）：｝，i＝1，2，…，N，从而使得p（θk（i）＝θk｜k-1（j））＝ωk（j）。

⑥加MCMC步骤。

3 仿真及试验结果分析

3.1 仿真信号的粒子滤波降噪

选择Matlab中的仿真信号Blocks，以此作为原始信号，信号长度为N＝1 000，在原始信号中叠加随机噪声，信噪比为2，图1为粒子滤波降噪结果。

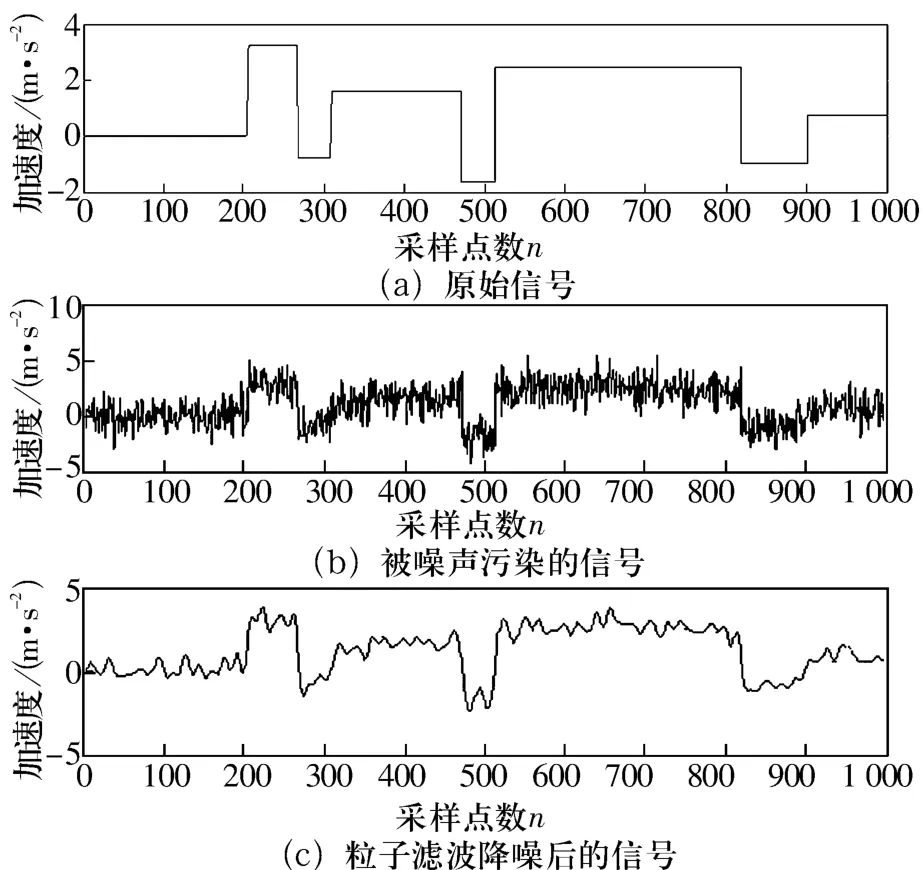
图1 粒子滤波降噪结果

仿真结果表明，粒子滤波能有效地滤除信号中的随机噪声，保留信号的真实性。

3.2 粒子滤波降噪在轴承故障诊断中的应用

试验中采用减速机输入端6206轴承，在不影响轴承正常使用性能的情况下，在轴承外圈上加工宽为0.5 mm，深为1.5 mm的小槽来模拟轴承外圈的局部裂纹故障。

试验时测试系统为LMS信号分析仪，振动传感器为B＆K4508，分析带宽为3.2 kHz，采样频率fs为8 kHz，采样点数为2 048，轴承内圈回转频率fr1＝10 Hz，粒子数为500。6206轴承的几何尺寸：球组节圆直径Dpw＝46.5 mm；钢球直径Dw＝9.5 mm；接触角α＝0°；钢球数Z＝9。

轴承外圈故障频率：

图2为滤波前、后外圈故障振动信号。对该故障轴承的振动信号进行倒频谱分析，如图3所示。在降噪前的振动信号倒频谱中难以找到外圈故障的特征频率，而在用粒子滤波降噪后的振动信号倒频谱中第223点处有一个明显的峰值，则故障频率f＝fs／n＝35.87 Hz，对应了轴承外圈故障频率35.81 Hz。

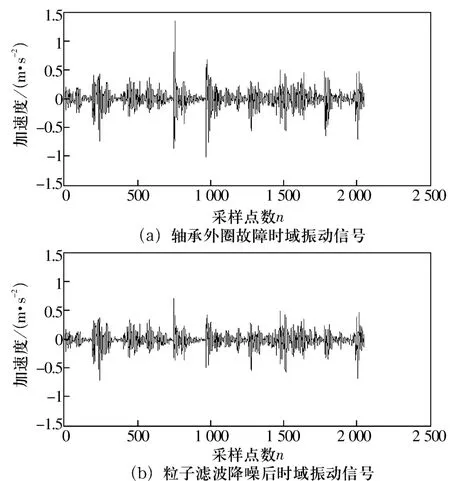
图2 滤波前、后外圈故障振动信号

图3 滤波前、后外圈故障振动信号的倒频谱

4 结束语

针对轴承振动信号容易受到较为复杂的非Gauss随机噪声的污染，提出了基于RBPF的振动信号降噪方法。建立了不含噪的振动信号的时变自回归模型，进而转化成对应的状态空间模型，把降噪问题转化成在状态空间模型下的滤波问题，并通过仿真和实测信号对其进行了验证。研究结果表明该方法可以有效地滤除轴承故障信号中的背景噪声，从而为后续的故障特征提取提供了可靠的数据保障。该方法不局限于噪声的Gauss假设，同时是一种实时处理的滤波方法，为轴承振动信号预处理提供了一种切实可行的方法。