大规模数据集分类算法探讨与优化
2010-07-25吕伟忠
吕伟忠
0 引言
数据分类是数据挖掘中的一种重要的分析方法。常见的分类方法有统计学分类法、决策树法、神经网络法、粗糙集方法和遗传算法等。相对其它的分类算法,决策树分类速度快、准确性较高、便于理解并且更容易转化成数据库访问语言,因此,决策树在数据分类方面有着广泛的应用。
对于大规模数据集,决策树分类算法在可伸缩性方面的主要问题是训练集受内存容量的限制。为此,在早期算法的基础上先后出现了SLIQ和SPRINT算法,他们重新定义了新的数据结构,降低或消除了内存限制,提高了算法的可伸缩性。但是,由于数据结构本身的原因,SLIQ没有从根本上消除内存的限制;而SPRINT算法由于仍然沿用对结点深度优先的递归算法,每次分裂都要对整个结点的数据重新存储,耗费大量I/O时间。本文接下来将对两种算法进行探讨与对比,文章的最后引入新的辅助数据结构,对SPRINT算法进行优化。由于篇幅所限,本文只对算法的数据结构以及算法的特点进行分析,具体的算法参见[3][4]。
1 SLIQ算法特点分析
对于数值性属性,在每个结点分裂时需要重新排序,这将消耗大量的CPU时间,为此SLIQ算法引进了新的数据结构,在算法的初始阶段将整个训练集按照属性进行分解,每个训练样本的同一种属性被分配在同一个列表中,称为属性列表,包含序号以及属性两个字段;每个训练样本的分类也被分配在同一个列表中,称为类列表,类列表除了类别以外增加了一个字段leaf,该字段表明样本当前所属的叶子结点,其值随着结点的分裂而动态变化。各列表间靠ID相联系。接着对所有数值性属性列表一次性排序。图(1)为汽车驾驶风险数据集的例子。

图1
属性列表的引入使得数值性属性的排序降低为一次,大大降低了算法的时间复杂度;结点的广度优先分裂算法跟属性列表以及类列表的结合,使得在结点分裂时无需重写训练集数据,只需要改变类列表的leaf字段,实现了训练集样本从物理分裂到逻辑分裂的转化,节省了相当的I/O时间;当前未被使用的属性列表可以暂存于磁盘,提高了算法的可伸缩性。但由于每次分裂时都要更改类列表的leaf字段,类列表只能常驻内存。因此,SLIQ没有从根本上消除内存的限制。
2 SPRINT算法特点分析
SPRINT算法在数据结构上继承了SLIQ的特点并进行了改进,把类列表融合到属性列表中,如图(2)所示,每个属性列表包含了3个字段:序号、属性以及所属的类。各列表间靠ID相联系。跟SLIQ一样,在算法的初始阶段对所有数值型属性列表一次性排序;当前未被使用的属性列表可以暂存于磁盘。由于取消了必须常驻内存的类列表,SPRINT算法从根本上消除了内存的限制。
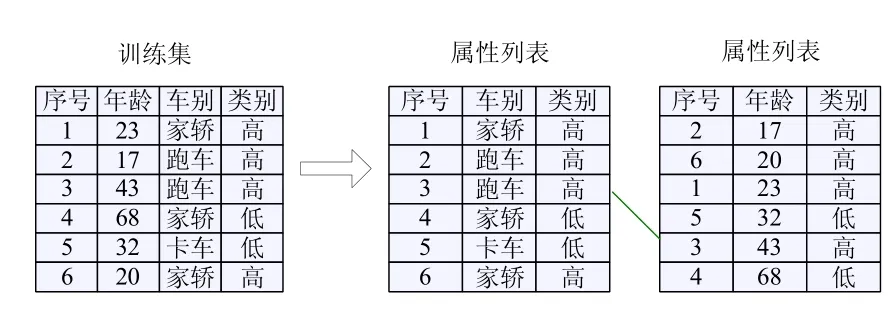
图2
与SLIQ不同,SPRINT仍然沿用了传统的深度优先的结点分裂方法,用自上而下的递归方式生成树。算法步骤如下:
a) 如果S满足停止扩展的条件,则返回;
b) 对于每一个属性Ai,找到Ai的一个值或值集Vi,它将产生以Ai为测试属性的最佳分裂;
c) 比较各个属性的最佳分裂,选择一个最佳的将S分裂为S1和S2;
d) 递归地对S1和S2生成决策树。
其中,S、S1、S2分别为结点所对应的集合,S1、S2为S的两个分支,最终生成的决策树是一颗二叉树。
该方法比较简洁,但是在结点分裂时需要为每个结点重写新的训练集,如图(3)所示。即需要对整个训练集进行多次物理分裂,这将消耗大量I/O时间,特别对于大规模的数据集。
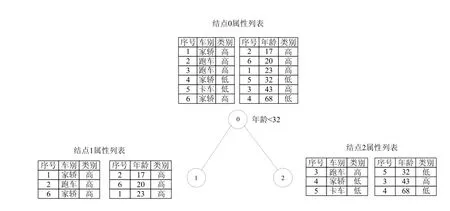
图3
3 对SPRINT算法的优化
对于大规模数据集分类算法,完全消除内存的限制并获得较高的处理速度,是比较理想的。为此,我们把SLIQ中对训练集进行逻辑分裂的思想引进到SPRINT算法中,对其进行优化。
在SPRINT原数据结构的基础上,对于每个结点,另建立相应的辅助数据结构—标志数组列表(BZ)。列表只有一个ID字段,若值为1,则表明该ID所对应的样本在该结点中,否则不在,如图(4)所示,BZ0所对应的结点为0结点,数组的每个元素的值为1,表明数据集的每个记录均在根结点中;BZ1对应的结点为1结点,数组元素1、2、6的值为1,表明它们属于1结点;同样3、4、5属于2结点。算法自始至终仅保存一套完整的属性列表,结点分裂时不再对属性列表进行重写,而是为每个子结点建立相应的标志数组列表,如图中所示。
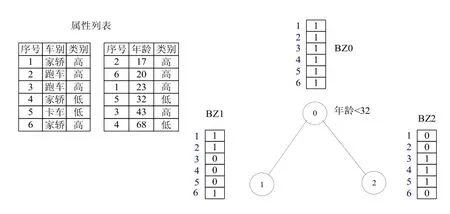
图4
对于某结点n,在对属性进行基尼指数评估时,由于没有实际的属性列表子集,可通过查找相应的标志数组列表并顺序扫描属性列表的方法来填写柱状图。对于离散值属性,因为属性列表与标志数组序号相同,均为顺序排列,可以很好的进行属性值的顺序扫描,其伪代码片段如下:
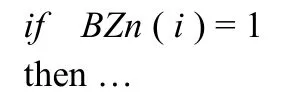
对于连续值属性,虽排序阶段顺序已经打乱,通过序号也可很好的进行判断扫描,其伪代码片段如下:
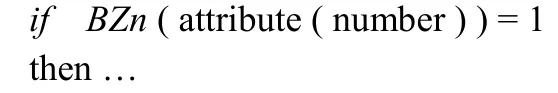
对于整个属性列表S:
算法步骤如下:
①如果BZ0满足停止扩展的条件,则返回;
② 对于每一个属性Ai,找到Ai的一个值或值集Vi(值或值集Vi的序号在BZ0中),它将产生以Ai为测试属性的最佳分裂;
③ 比较各个属性的最佳分裂,选择一个最佳的将BZ0分解生成BZ1和BZ2;
④ 递归地对BZ1和BZ2生成决策树。
其中,BZ0、BZ1、BZ2分别为结点所对应的标志数组列表,BZ1、BZ2为BZ0的两个分支,最终生成的决策树是一颗二叉树。
4 算法比较
SPRINT算法在结点分裂时需要重写数据集,这是影响算法速度的重要因素,但在对每个属性进行基尼指数评估的时候针对的是一个实际存在的数据子集;优化的SPRINT算法继承了原算法的诸多优点,并且对整个数据集进行逻辑分裂,完全省去重写数据付出的I/O时间,但在对每个属性进行基尼指数评估的时候需要对整个数据集进行查表,这将额外增加计算量,为此我们用UCI[5]提供的实验数据对其进行实验比较,实验结果如图所示:
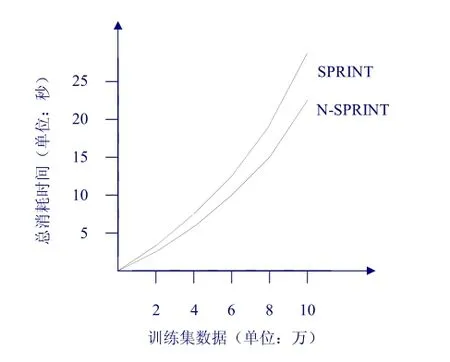
图5
实验结果表明,优化后的SPRINT算法在计算速度上确实有了一定的提高。
5 结束语
大规模数据集分类算法是数据挖掘中广为研究的课题之一,本文对两种最具代表性的算法SLIQ和SPRINT进行了讨论与比较,针对SPRINT的局限性,引进了SLIQ中对属性列表逻辑分裂的思想对其进行了优化和测试。实验结果表明,优化后的SPRINT算法在计算速度上有了一定的提高。但实验只是局限在串行阶段,并行算法的优化有待于进一步的实验。随着数据库规模的日益增大,数据信息日渐复杂,大规模数据集分类算法将是今后研究的一项重要内容。
[1]Karrber M J H,数据挖掘概念与技术[M].范明,孟小峰,译.北京:机械工业出版社.2001.
[2]Quinlan J R. C4.5: Programs for Machine Learning[M].Morgan Kaufman,1993.
[3]Mehta M, Agrawal R,Rissancn J.SLIQ:A Fast Scalable Classifier for Data Mining[C]//Proc.of the 5thInt’l Conf.on Extending Database Technology,Avignon,France,1996-03.
[4]Shafer J,Agrawal R,Mehta M.SPRINT:A Scalable Parallel Classifier for Machine Learning[C]//Proc.of the 22thInt’l Conf.on VLDB,Bombay,India,1996-09.
