正弦交变电流有效值的简单推证

石 莹

(甘肃省积石山县第一中学,甘肃积石山 731700)

交流的有效值是根据电流的热效应规定的.让交流和直流通过相同阻值的电阻,如果它们在相同的时间内产生的热量相等,就把这一直流的数值叫做这一交流的有效值.课本中就是这样给出交流有效值的概念后直接引入了正弦交变电流有效值的公式.但对公式没有进行推导.虽然教参上用高等数学知识给出了详细推证,但中学生很难接受,本文用适合于中学生的初等数学方法进行推导,帮助学生搞清公式的来龙去脉,对学生彻底地理解有效值的含义是十分有益的.下面将介绍两种简单推导方法,供读者参考.

1 初等理论推导法

假定让一直流和一交流分别通过相同阻值的电阻 R,经过相同的时间T(T是这一交流的周期),直流所产生的热量为 Q1=I2RT,设在周期 T内交流的平均功率为¯P,那么交流所产生的热量为 Q2=¯PT.如果 Q1=Q2,即 I2RT=¯PT,那么 I就是交变电流的有效值,则有

设交变电流i=Imsinω t在周期T内的瞬时功率为P,则

由(2)式可知,交变电流的瞬时功率等于两项的和,第1项是不随时间变化的常量,第2项是按余弦规律变化的变量.第1项就是交变电流平均功率,而第2项是一个余弦量,有时为正,有时为负,在一个周期内的平均值等于零.因此交变电流在一个周期内的平均功率是将(3)式代入(1)式,得再结合欧姆定律,就可以得到

2 图像面积割补法

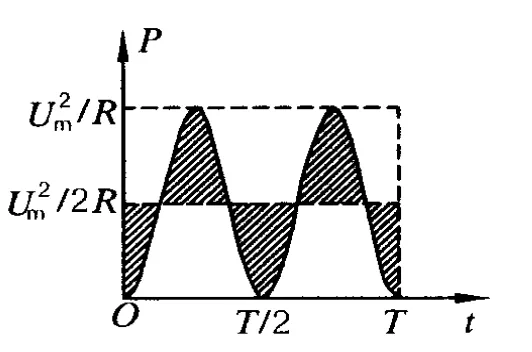
图1

当交变电压u=Umsinω t对电阻供电时,通过电阻 R的电流为i=该交变电流的瞬时功率为

根据(4)式可画出瞬时功率 P与时间t的关系图线如图1所示.

因为电功 W=Pt,所以交变电流在一个周期内对 R所做的功W为P-t图线中曲线与t轴所围的面积,利用图像的割补,可得知所以.当直流电压U对电阻R供电时,在一个周期内对R所做的功为则有即得再结合欧姆定律,就可以得到

上述两种推导方法简单明了,帮助学生搞清了正弦交变电流有效值与最大值关系式的来源,进一步深化了有效值概念的理解.