“形同质异”的物理问题处理

翟孝影

(江苏省徐州市侯集高级中学,江苏徐州 221121)

在物理习题处理中,我们常会遇到一些形相似而实质却不相同的问题,很多学生不加注意把头脑中原问题的解法直接迁移过来进行解答,结果形成错误.这些问题看似相同但实质却大相径庭,弄清这些问题的差异,充分挖掘题目中的隐含条件,将有利于提高学生分析问题、解决问题的能力.

1 “动杆”和“定杆”问题

例1.如图1-1所示,质量为 m的物体用细绳OC悬挂在支架上O点,轻杆OB可绕B点转动,求细绳OA中张力T的大小和轻杆OB受力N的大小.

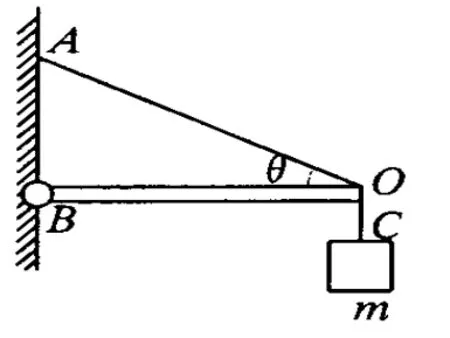
图1 -1

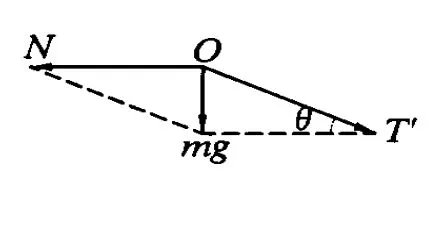
图1 -2

解析:由于轻杆 OB可绕B点转动(即是“动杆”),所以细绳对轻杆OB的力一定沿着杆的方向,否则杆就不能平衡(即要发生转动).由于悬挂物体质量为 m,所以绳OC拉力大小就等于mg,将这个拉力沿杆和 AO方向分解,如图1-2所示.由图即可求得

例2.如图2-1所示,水平横梁一端 A插在墙壁内,另一端装有小滑轮B,一轻绳一端C固定于墙壁上,另一端跨过滑轮后悬挂一质量为 m=10 kg的重物,∠CBA=30°,(g取10 N/kg)则滑轮受到绳子作用力为

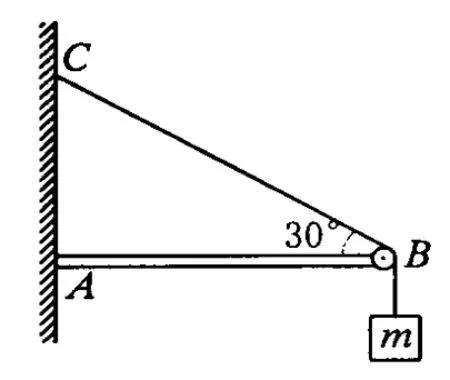
图2 -1

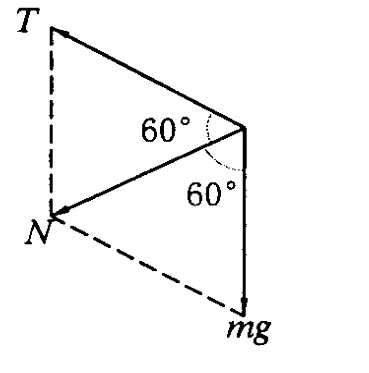
图2 -2

解析:由于杆 AB不可转动(即是“定杆”),所以杆所受弹力的方向不一定沿杆 AB方向.由于 B点处是滑轮,它只是改变绳中力的方向.并不改变力的大小,滑轮两侧绳上的拉力大小均是 100 N,夹角为120°.故滑轮受绳子作用力N即是两拉力的合力,如图2-2所示.

由图可知,滑轮受到绳子作用力的大小为N=T=mg=100 N.所以选项(C)正确.

评价:这里我们要注意杆是否能转动.能转动且处于平衡,杆上力的方向一定沿杆,不能转动且杆处于平衡,则杆上力的方向有任意的可能.

2 “活结”和“死结”问题

例3.如图3-1所示,长为5 m的细绳的两端分别系于竖立在地面上的相距为4 m的两杆的顶端 A、B,绳上挂一个光滑的轻质挂钩,其下连着一个重为12 N的物体,平衡时绳中的张力 T为多大?当 A点向上移动少许,重新平衡后,绳与水平面夹角、绳中张力如何变化?

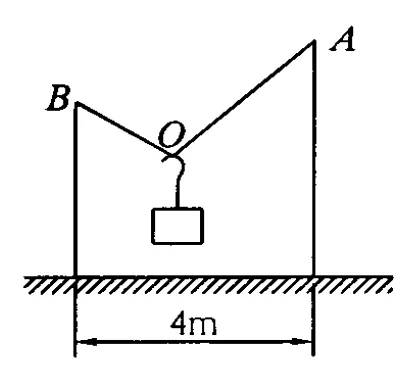
图3 -1

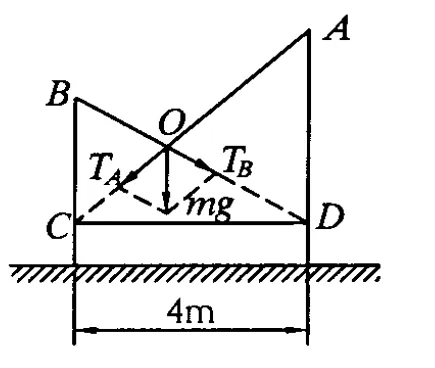
图3 -2

解析:设重物平衡时悬点为 O,延长 AO交B杆于C点,从C向A杆作垂线CD交A杆于D点,如图3-2所示.由于挂钩光滑,所以挂钩两侧绳 AO段与BO段的拉力必然相等,与竖直线的夹角也相等,因而 OB=OC,故 AC=5 m,设∠A=α.则

取O点为研究对象,将重物对O点的拉力沿AO、BO延长线分解为TA、TB,即有 TA=TB=T.由图 3-2和平衡条件可得 2Tcosα=mg,可解得 T=10 N.

同样分析可知:当 A点向上移动少许重新平衡后,绳与水平面夹角及绳中张力均保持不变.

评价:因为绳上挂的是一个轻质光滑挂钩,它可以无摩擦地滑动(因是“活结”),所以挂钩两侧的绳(其实是同一根绳)的形变相同,拉力也必然相等.

例4.用3根轻绳将质量为 m的物块悬挂在空中,如图4-1所示.已知 ac和bc与竖直方向的夹角分别为 30°和60°,则 ac绳和bc绳中的拉力分别为

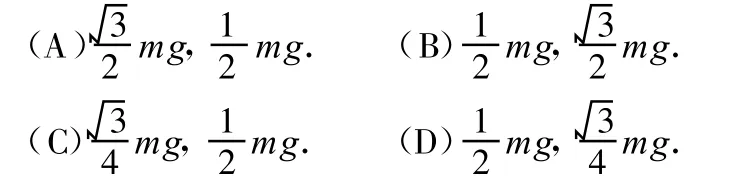
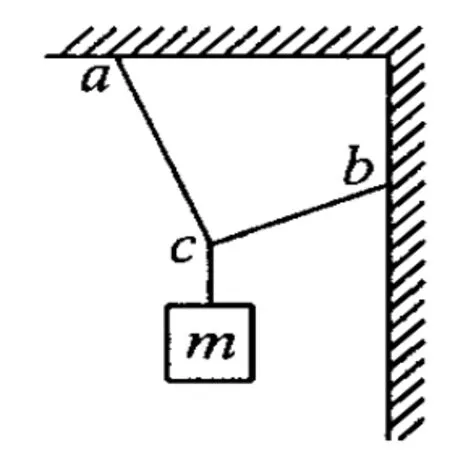
图4 -1

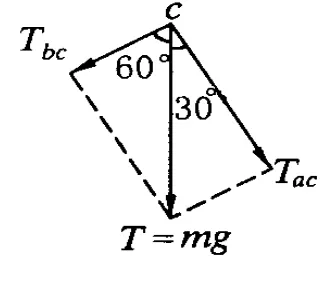
图4 -2

解析:以绳子的结点 c为研究对象,它受3个拉力的作用而处于平衡状态.将重物对c点的拉力分别沿ac绳和bc绳方向分解为Tac、Tbc,如图4-2所示.

由平衡条件和图中几何关系可得

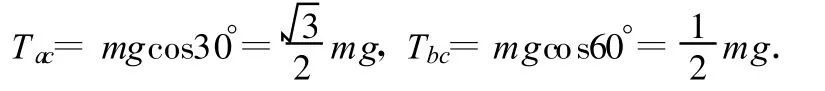
所以选项(A)正确.

若将b点向上移动少许,重新平衡后,绳 ac、bc的张力均要发生变化.

评价:因为3根轻绳的结点是不能滑动的(因是“死结”),所以结点两侧绳的形变一般不同,拉力一般也就不相等.

3 “轻绳”和“轻杆”问题

例5.如图5所示,长为 l的细绳一端固定在O点,另一端系着一个质量为 m的小钢球,小钢球可视为质点,首先将小钢球拉到图示的 A位置,然后无初速度释放,求当细绳摆至竖直位置时,小球的速度为多大?

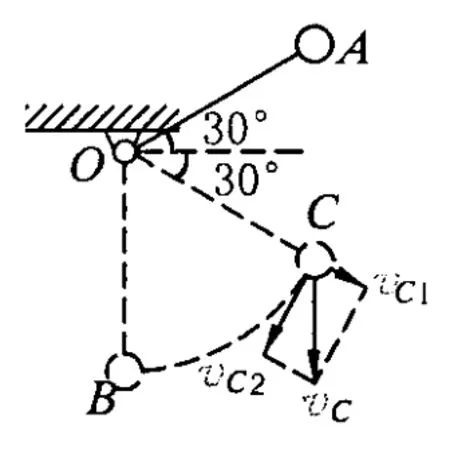
图5

解析:第1个过程:小钢球从 A点下落到C点时,根据机械能守恒定律,有

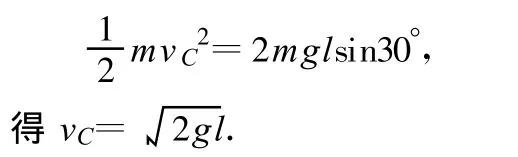
第2个过程:小球在 C点的速度vC,可分解为沿绳子方向的速度和垂直绳子方向的速度(如图5),其中在沿绳子方向

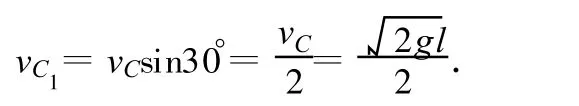
此速度在C点由于绳被拉紧,受绳的拉力作用而很快变为零.在这个很短的过程中就有动能损失,其损失的动能为

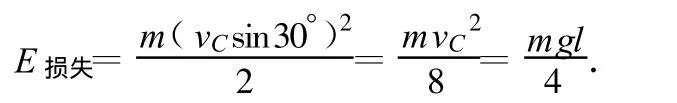
小球垂直于绳子方向的速度

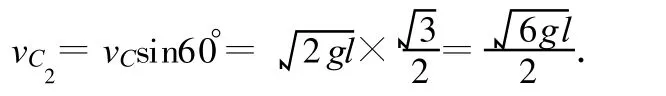
第3个过程:小球自C点以vC2的速度沿圆弧运动到B点,但此过程中,绳的拉力始终与球的运动方向垂直,不做功,只有重力对小球做功,故此过程中机械能守恒.在 C点,小球动能重力势能 Ep=mgl(1-cos60°),在 B 点,小球动能重力势能为零.由机械能守恒定律有 Ek1+Ep1=Ek2,即解得

引申:如果将上述中的绳换成轻杆呢?

解析:小钢球从A点到C点再到B点整个过程杆对小球都不做功,根据机械能守恒定律mvB2,解得

评价:比较上述两题的共同之处,都是分析放在同一高度处的小球从静止开始下落,不同之处是,一个是轻杆,一个是轻绳.“轻杆”在整个过程中对小球不做功,只有重力做功;“轻绳”问题中,小球在下落过程中绳绷紧瞬间,绳子拉力做功.因此我们在分析题目时.一定要抓住题目中隐含的条件,找出本质区别.

4 “轻绳”和“轻弹簧”问题

例6.如图6-1所示,物体在轻绳和轻弹簧作用下均处于平衡状态,图中细线不可伸长.如果突然把两水平细线剪断,求剪断瞬间小球 A、B加速度怎样?(θ角已知)

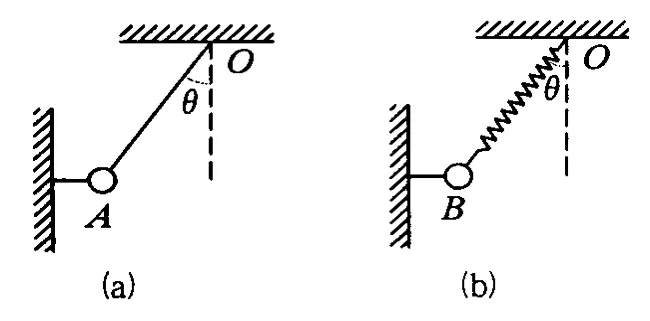
图6 -1

解析:对 A球进行受力分析,如图6-2(a),剪断线后,小球将做圆周运动,则剪断瞬间小球的加速度a1方向沿圆周切线方向,其大小

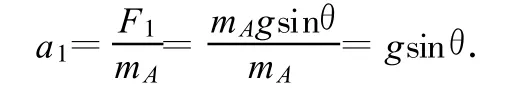
对B球进行受力分析,水平细线剪断瞬间,B球受重力G和弹簧弹力F′,且大小不变.如图6-2(b)所示,则 F2=mBgtanθ,所以 B球的加速度a2方向水平向右,a2=gtanθ.

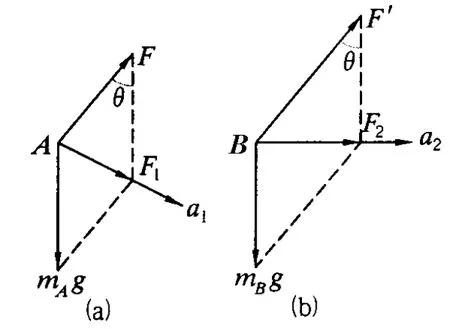
图6 -2

评价:对于细绳和轻弹簧(包括弹性绳)的力的分析,要注意细绳弹力可以发生突变而弹簧弹力不能发生突变,另外还要结合物体的运动状态重新进行受力分析.

综上所述,在处理“形同质异”的物理问题时我们一定要注意审题,抓住处理问题的本质,要注意区别,明确处理方法,以求得正确解答.