加速度不能套用速度分解的模式

王 锴

(四川省万源中学,四川万源 636350)

1 问题的来源

笔者现任教高三物理课,在某次月考时,发现试卷中有这样一道题:

如图1所示,一条轻绳跨过定滑轮两端,左端连接一个重物,右端连接一个小车.小车在水平面上做匀加速直线运动.问以下说法哪些是正确的.

(A)重物所受细绳拉力大于重物的重力.

(B)重物所受细绳拉力小于重物的重力.

(C)重物做变加速运动且加速度不断变大.

(D)重物做变加速运动且加速度不断变小.

题目所给的答案为(A)、(C).经分析,可把小车的速度分解为沿着绳子方向的分速度 vr和垂直于绳子方向的分速度vt.而轻绳左端重物向上运动的速度vm就等于沿着绳子方向的分速度vr,根据速度分解关系有

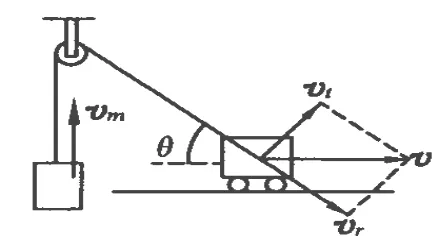
图1

当小车向右运动时,θ角不断变小,所以cosθ不断增大,且小车的速度 v又不断增大,所以重物向上运动的速度vm不断增大,可推知重物向上做加速运动.所以重物所受细绳的拉力大于重物的重力,故(A)选项正确.但是(C)选项就值得商榷了.出题者的原意是:把以上分析速度的方法推广到两物体的加速度.即认为重物的加速度 am也等于小车的加速度沿绳方向的分加速度ar.以致得出重物加速度也不断增大的结论.笔者认真查阅了大学的力学教材.发现问题没有那么简单.结论是:加速度不能套用速度分解的模式去解算.

2 问题的分析及解决

如图2所示,以绳端为原点建立自然坐标系,其中er表示沿着绳伸长方向的单位矢量,et表示垂直于绳子方向的单位矢量.

本问题的以上解法错在简单地认为重物的加速度am也等于小车的加速度沿绳子方向的分加速度ar.实际上,由于小车的两个分速度 vt和vr都在发生变化,而且都包括大小和方向两方面的变化.所以小车的加速度应该有4个分量,分别为:小车沿着绳子方向的分速度vr的大小变化产生的加速度vr的方向变化产生的加速度;小车垂直绳子方向的分速度 vt的大小变化产生的加速度以及 vt的方向变化产生的加速度.

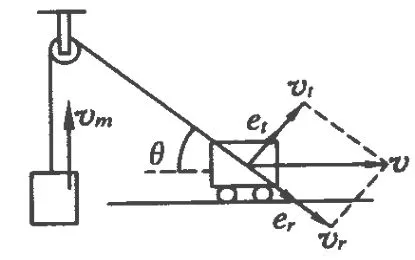
图2

用矢量分析公式来计算小车的加速度有

根据矢量分析相关公式有

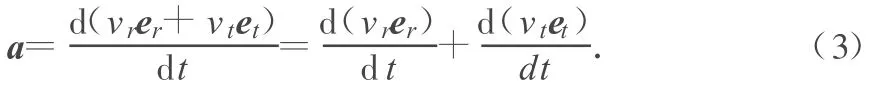
进一步有

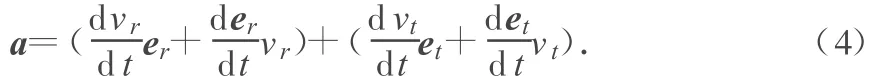
最后有

整理可得

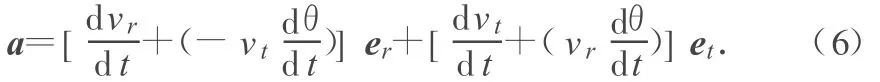
从计算结果可以看出,其中小车沿着绳的方向的分速度vr的大小变化产生的加速度和小车垂直于绳子方向的分速度vt的方向变化产生的加速度沿着er的方向即绳子的方向,且与er同向即沿着绳伸长的方向,与er方向相反,即沿着绳伸长的反方向.同理在垂直于绳子方向上也包括vr的方向变化产生的加速度和vt的大小变化产生的加速度且二者是同向的.

其中vr的大小变化产生的加速度和vt的方向变化产生的加速度二者的矢量和才等于小车的合加速度沿绳子方向的分量.即有

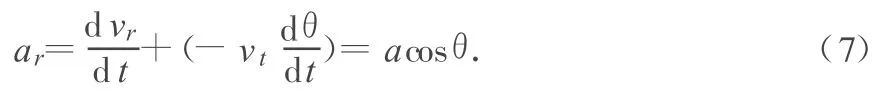
而根据绳长不变,只有vr的大小变化产生的加速度才等于重物上升的加速度.这个加速度并不等于小车沿绳子方向的分加速度.即

那么重物上升的加速度究竟是多少呢?应该说这和问题的具体情况有关.为了简化分析,在不违背题意的前提下,我们可作如下假设,如图 3所示.

假设小车的初位置在定滑轮下方,即计时开始时轻绳两边均处于竖直状态.且右边绳长为H.并设小车从静止开始以加速度a做匀加速直线运动.则有重物的加速度为

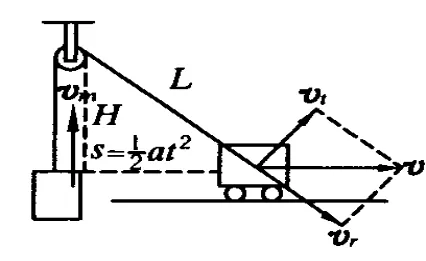
图3

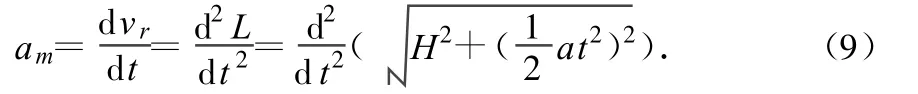
经计算可得

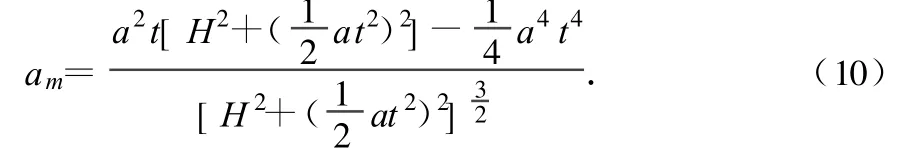
其实既然vr的大小变化产生的加速度和vt的方向变化产生的加速度的矢量和等于小车的加速度沿绳子方向的分量,那么以上结论可以简化为

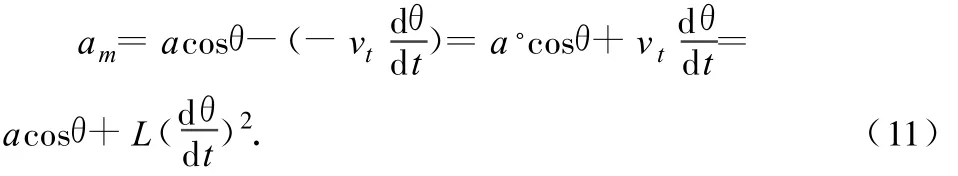
可见重物的加速度随时间的变化是十分复杂的一个函数,我们可以得出结论:重物的加速度随时间并不是简单地增大或减小.随着参数取值的不同,有可能是在某些区间内加速度增大,而在另一些区间内加速度却要减小.即使随时间一直增大,这个结论的复杂程度也远远超出了中学生能解决的程度.

3 结论及分析

通过对以上问题的分析我们可以看出,由于加速度是物体位矢对时间的二阶变化率.对于加速度的分析计算,不能简单地照搬分析速度的方法和结论,必须考虑到速度矢量的大小的变化和方向的变化均能产生加速度.在分解加速度时更要想清楚,分加速度的物理意义,不然就会得出错误的结论.

1 赵凯华,罗蔚茵.新概念物理教程◦力学(第2版).北京:高等教育出版社,2004.23

2 强元户攵木.经典力学.北京:科学出版社,2003.7.

3 谢树艺.工程数学矢量分析与场论(第2版).北京:高等教育出版社,1985.9