二维混凝土骨料类型的数值模拟

2010-07-24邵海成周立明胡建强项利南

天津建设科技 2010年3期

□文/邵海成周立明胡建强项利南

对于三级配或全级配混凝土，湿筛法导致混凝土的组成比例发生了变化，尤其水泥砂浆和骨料含量的比例，因此试件的力学性能不同于实际情况下的力学性能。通过试件确定的所有力学指标都不能真实反应实际结构的力学指标，在结构的设计和施工中将出现不精确性。因此，结合一定数量的试验，需要通过使用微级数值模拟方法来研究大体积混凝土的性质。

混凝土的数值模拟主要集中在骨料形状的模拟上。建议采用几种模型来预测混凝土的性质。第1个是随机骨料模型，这个模型经常用来模拟固体颗粒材料；第2个模型是随机填充颗粒模型，它是用来模拟波特兰水泥混凝土的；第3个是一个随机二维天然形状骨料模型，它为混凝土数值模拟的进步做出了巨大贡献；第4个是网格模型，由于计算能力的不精确性它并没有投入实际应用；第5个是梁-颗粒模型，该模型是由在离散元法的基础上开发出来的。

为了得到更多的混凝土的真实特性，采用一个更精确的方法来模拟骨料形状是非常必要的。

生成任意多边形的算法

任意三角形的生成

首先同时设置相同直径的任意排列圆形，用来控制三角形基本骨料的尺寸和位置。骨料的直径决定圆形的半径。三角形基本骨料的生成是建立在这些任意排列的圆形的基础上。方法描述如下：

（1）在每个圆形的轮廓线上随机的生成3个点；

（2）在动态三角形中，通过控制角度的余弦值来生成一个锐角三角形。

然后，根据三角形基本骨料可以生成任意多边形骨料，见图1。任意三角形基本骨料决定了骨料的直径和最终几何形态。

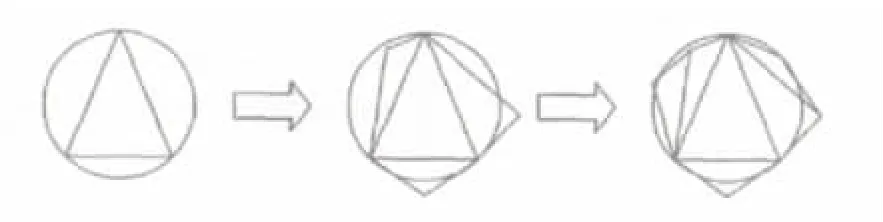
图1 三角形骨料的任意延伸

延伸条件和方法

多边形的延伸条件：有一个边，它的长度至少要大于极限值Lmax。在以这条边为直径的半圆中生成一个新的顶点p，如图2所示。p的坐标计算如下：

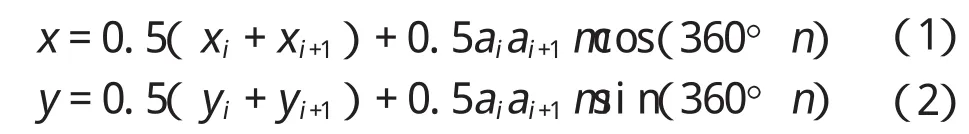
式中：m和n分别表示0～1的随机数字。在公式（3）中如果S＞0，则p位于半圆内侧。如果S大于三角形aiai+1p′的面积，那么p将不会位于三角形aiai+1p′的内侧并且多边形的形状将接近于实际骨料形状。见图2。三角形aiai+1p′的面积计算

通常情况下，实际骨料经常显为凸形。因此，本文中的算法也受限于骨料的凸形。由于这个限制，p将限制于2倍基本骨料直径的距离之内。为了确定两个颗粒之间是否存在重叠，唯一要做的是：确定两个相邻圆形中心之间的距离。如果这个距离大于2倍的直径，那么两个颗粒还没有彼此重叠。由于没有必要一一确定这个条件，所以这样很大程度上提高了效率。

多边形的重叠准则

角度之和的计算

分别连接p和a1,a2,…,an。θi表示∠aipa+（1i=1，2，…，n-1），表示。如果表示p位于多边形a1,a2,…,an外，见图 3a；如果，表示p位于多边形a1,a2,…,an内，见图3b，其中通过余弦定理可以计算θi，它的正负定义如下，以∠a1pa2为例。

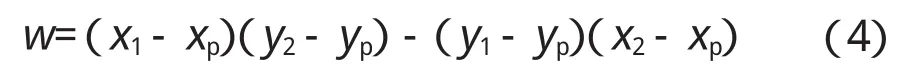
如果w＜0，角度的方向为顺时针，则θi是负的；相反如果w＞0，角度的方向为逆时针，则θi是正的。

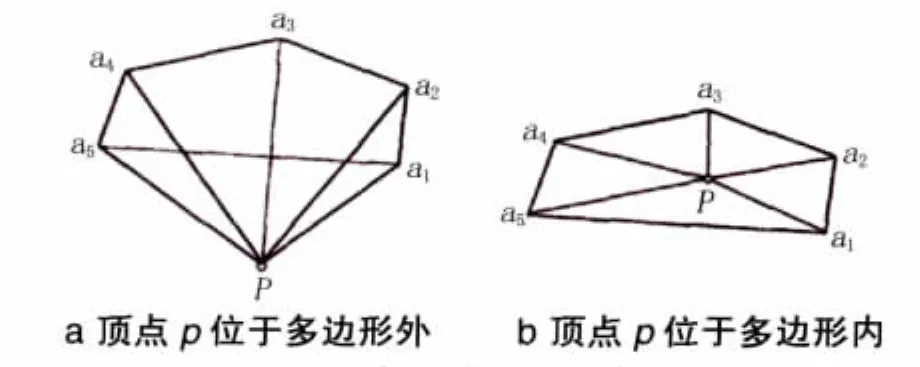
图3 p与多边形之间的关系

检测相交

为了避免特殊情况，如图4所示，有必要确定两条边是否相交。通过分别连接p和ai、ai+1，可以使每条直线有两个方程。当这些方程中的每一个都结合了直线a1a2,a2a3,a3a4,a4a5和a5a1的方程中的一个时，通过使用克拉默法则就可以获得交点的坐标，然后就可以给出这个点是否在骨料轮廓线上的判定标准。

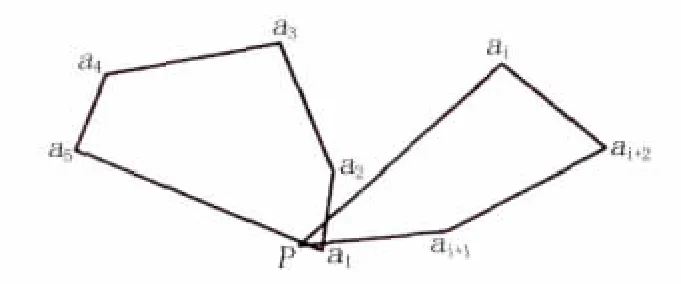
图4 两个多边形相交的特殊情况

凸度条件

对于任意多边形，确定多边形的凸度是一个临界控制条件。这个条件可以确保p将不会无限制的延长。因此在这个算法中必须提供凸度条件，使（x1，y1），（x2，y2）和（x3，y3）分别成为某个特定三角形 3个顶点的坐标，这些点以逆时针顺序排列，然后三角形的面积可以表示

如图5所示，在这些已有边的条件下插入p来形成多边形的新边。凸度条件是三角形的面积受制于点p和对边，基于公式（5）边ai-1ai或ai+1ai+2必须是正的。

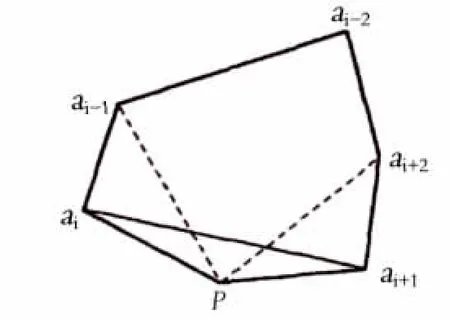
图5 三次延伸后新的顶点p

骨料交界面的生成

本文交界面生成的方法不同于在盘状颗粒中使用的方法，对于交界面，在此方法中限制了两个相邻颗粒中心间更长的距离，以此来预留空间。在现有的方法中首先生成大骨料，然后标定它的尺寸来形成交界面，见图6。根据相似三角形原理就很容易计算骨料所有顶点的坐标。

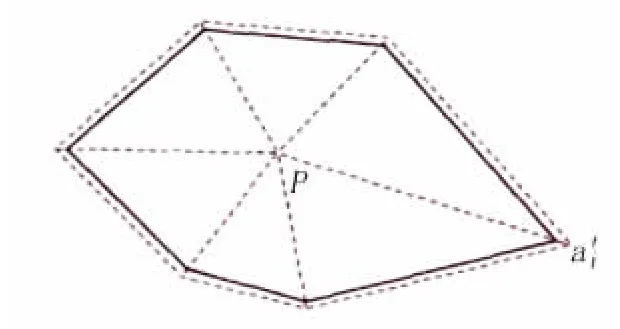
图6 骨料的交界面

2D-RAS的主要步骤

（1）根据骨料含量和一种级配骨料的平均直径，计算骨料的数量。

（2）生成所有随机数字来确定所有骨料的位置，然后将所有的基本骨料一次安放于混凝土截面。

（3）检查所有基本骨料的重叠部分。如果没有重叠部分，则进行步骤4，否则重复步骤2和3。

（4）为每个基本骨料生成延伸骨料。任意骨料的生成也需要检查重叠和交叉的条件。

（5）对于下一级配，重复上述步骤，从而生成全级配混凝土（或三级配混凝土）的模型。

使用软件2D-RAS生成了骨料含量为65%的任意骨料模型，见图7。

图7 骨料含量为65%的随机骨料模型

数值算例与讨论

非线性本构模型

考虑到准脆性材料的破坏并不是完全脆性，而是在达到极限强度后显示出一些延展性。事实上，在开裂末端前存在一小区域，而正是在此区域发生微裂缝的发展和聚结。本文将使用准脆性破坏本构模型来模拟砂浆和交界面的开裂破坏，该模型由内聚力可以表示如下

式中：f t表示材料的极限强度，Gt表示开裂能。骨料被看做线弹性材料。开发了有限元软件ABAQUS，用以执行一系列数值分析。在这个计算中，为复合材料的每一相都运用了非线性本构模型，见图8。

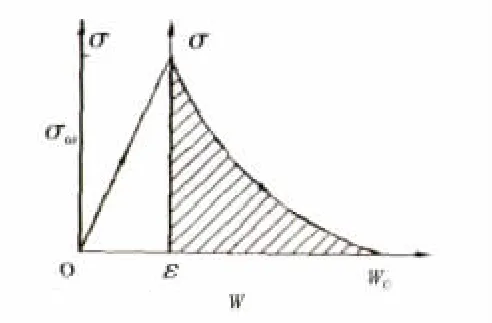
图8 材料的本构模型

三级配混凝土的单轴拉伸试件

随机骨料模型

本文中所研究的试件的尺寸为450 mm×400 mm，见图9。由软件2D-RAS生成的随机多边形骨料模型见图10a，图10b所示为随机盘状骨料试件。两个模型具有相同的骨料含量。表1中给出了计算中所采用的材料参数。

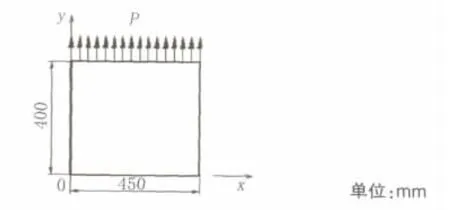
图9 试件的几何尺寸和荷载作用

图10 破坏时裂缝的传播和开裂模式

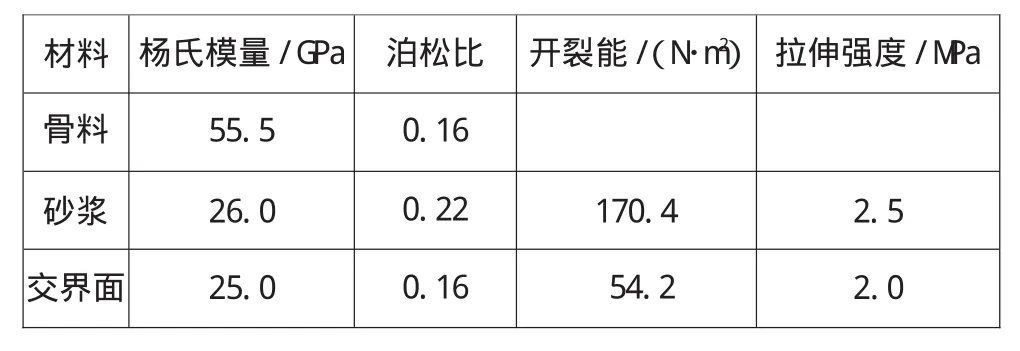
表1 分析中所采用的材料参数

结果和讨论

通过位移来控制拉伸荷载，从而模拟软化阶段混凝土的非线性材料影响。由于应力集中现象非常明显，在任意多边形骨料的混凝土试件中将很早就出现裂缝。这些试件中，在一个骨料的交界面单元将首先发现微裂缝，因为它的极限强度低于砂浆的强度。当荷载增加时，交界面出现了越来越多的破坏单元，而且在砂浆中也发现了一些破坏单元。最后，通过连接破坏单元而形成一条宏观裂缝，从而导致试件完全破坏。

多边形骨料试件计算的极限拉伸强度是1.61 MPa，而盘状骨料试件计算的极限拉伸强度是1.66 MPa，见图 11。

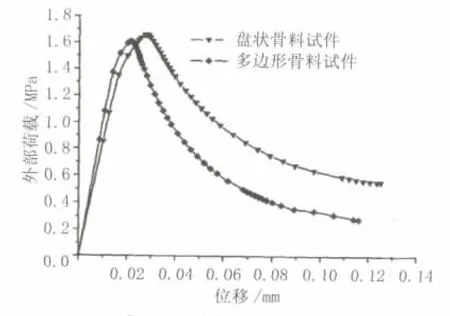
图11 荷载—位移曲线

任意多边形试件的结果明显比盘状颗粒试件的结果更接近试验结果。与多边形骨料试件相比，盘状骨料试件的极限荷载要大3%。

三级配混凝土的弯曲试件

随机骨料模型

这部分给出的例子是尺寸为300 mm×1 100 mm的一个弯曲单一支持梁，粗、中、细骨料的代表直径分别为60、30、12.5 mm。三级配混凝土大、中、小骨料的比例为4∶3∶3。骨料的密度为2.8×103kg/m3。梁的中间部分（尺寸为300 mm×200 mm）为多相复合材料。大颗粒盘状骨料、中颗粒盘状骨料、小颗粒盘状骨料的数量分别为3、10、68。当任意形状多边形模型生成之时，大骨料、中骨料、细骨料的面积分别为7 800、6 780、8 400 mm2。两种随机骨料模型均由2D-RAS软件生成。在分析中每相所采用的材料参数（除了两端混凝土的弹性模量和泊松比分别为30.0 GPa和0.17）也与第一个例子中所采用的材料参数相同。混凝土中的材料（骨料）也被认为是线弹性材料。两种情况下的骨料级配和含量也都相同。