基于泊松分布的需求预测模型设计

于建梅 （上海交通大学，上海 200030）

在稳定状态下，假设某物料的需求分布密度服从参数为λ的指数分布，则其需求率为常数λ，其发生需求的概率可由泊松分布的有关公式确定。

若平均每客户对公司产品在时间（0,t）的需求遵从参数为λt的泊松分布，即在时间（0,t），为满足每客户的需求，生产部门平均对该物料的需求数为K的概率为：

式中

Pk——对某物料需求为K的概率

K——对某物料的需求

t——计算时间

λt——时间0,（）t内物料的客户需求

1 物料需求量计算模型

需求量的确定是整个物料管理的关键问题之一，与需求量相关的参数有：

PN——平均每客户产品需求数 （件）

MN——每单位产品耗用材料数 （件）

N——客户数量 （个）

R——平均需求率 （次/天）

T——计算间隔时间（天）

α——计划保障率

λt——客户对公司产品在时间0,（）t的需求

K——生产部门对该物料的需求

RN——单位时间 （天）的平均客户需求数

由以上参数，可以计算出单位时间 （天）的平均客户需求数RN：

时间T内物料的客户需求λt：

于是该物料的生产需求K就是在保障率α下满足下式的最小整数：

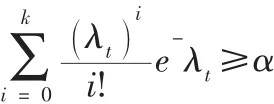
从以上的模型中，我们可以看出，在物料需求量的计算公式中，直接变量只有λt一个，而其决定因素中，PN、MN、N和T都比较容易得到的 （其中PN可以由历史数据获得），只有产品的平均需求率R是比较不容易得到的。

2 时间序列法在需求率预测中的应用

对需求率R值的预测可采用时间序列法，计算流程如图1所示：

（1）计算R的季节指数

设Yt为t期的实际值，N为周期数，Mt为t期的预测值，移动平均法的公式为：

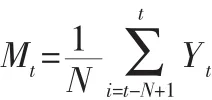
式中

Mt——t期的预测值

N——移动周期数

Yt——t期的实际值

移动平均数排除了实际值因季节因素引起的差异和部分随机因素的影响，可以作为长期趋势估计值，即Mt=t。

用实际值除以趋势值，就可以得到季节指数

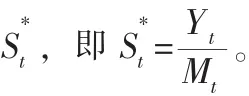
（2）计算R值的长期趋势

常用的趋势预测模型为线性趋势模型：

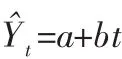
式中

t——时间

a、b——方程的参数

用最小二乘法导出的标准方程组为：

联解这个方程组，就可以求出参数a、b。

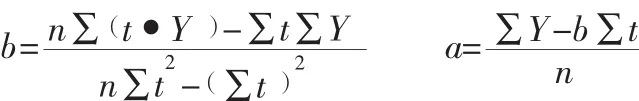
3 通过模型对需求量预测

假设某物料 2009年 7月 R的预测值为 0.16（次/天），在这一阶段的其他数据如下：T＝7；PN=30；MN=1；N=150；α=92%。

根据以上数据，我们可以预测出在2009年该部件的平均每天客户需求数RN：

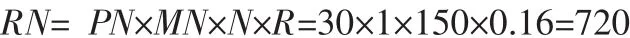
订货周期的λt：

将λt和 α值带入公就有：

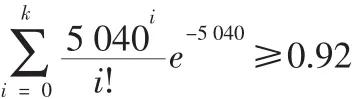
查泊松分布表，可得：K=5 139（件）。即在7天的订货周期内，该物料满足92%的保障率的生产需求量预计在5 139件。

[1]马庆国.管理统计——数据获取、统计原理、SPSS工具与应用研究[M].北京：科学出版社，2004:182-202.

[2] 张毅.南方航空公司河南分公司航材库存管理模型应用研究[D].武汉：华中科技大学，2007:25-53.