泡沫金属直流电位法检测技术

张 静，解社娟，陈振茂

（西安交通大学 强度与振动教育部重点实验室，西安 710049）

图1 泡沫金属示例

泡沫金属（图1）具有轻质、比强度高、比表面积大、隔音、隔热和电磁屏蔽等优点，在航空航天、汽车、军事等诸多领域具有广泛的应用前景[1]。在泡沫金属的制备过程中，由于条件控制不良等因素，可能造成多个孔泡相互融合形成大孔缺陷，若实际使用可能造成严重后果。因此，泡沫金属使用前须对材料进行定量无损检测。

直流电位检测方法（DCPD）由于没有集肤效应，电流可进入材料内部，在缺陷部分形成扰动[2－5]，并引起检测面电位分布的变化。通过检测这一变化可以推断材料内部缺陷的存在和大小，因此直流电位法有望成为泡沫金属内大孔缺陷检测的有效方法。图2为直流电位法的示意图。

为确定直流电位法检测实际泡沫金属缺陷孔洞及大小的有效性，对实物泡沫金属进行了直流电位法无损检测试验。同时为确定有效的试验条件，还运用有限元程序对检测信号进行了数值模拟。

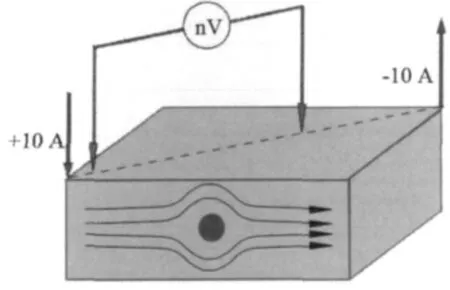
图2 直流电位法示意图

1 数值计算

1.1 有限元程序简介[6]

恒流场中基本方程[7]：

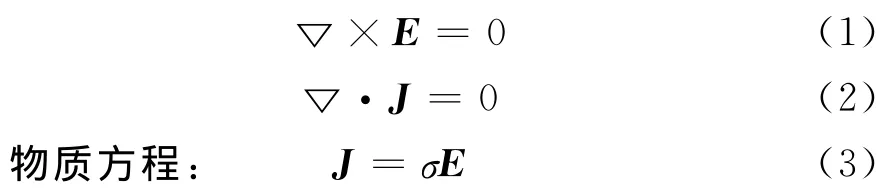
式中：E——电场强度矢量；

J——电流密度矢量；

σ——导体的电导率分布函数。

由上式可得如下恒流场控制方程：

选用立方体八节点等参元和伽辽金有限元法对式（4）进行离散求解。利用单元刚度阵：

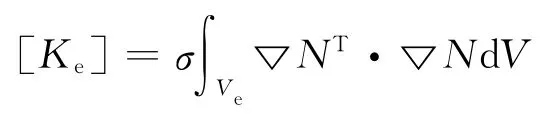
可得恒流加载时的有限元方程：

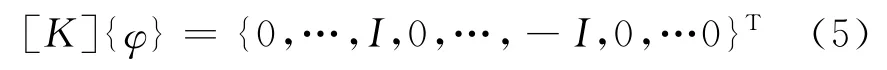
式中I和－I分别为加载点的流入和流出电流。

当恒压加载时，只需把加载点相应方程换为φi＝φ0，再把其他方程中的未知数φi换成加载电位φ0，并乘以系数后移到右端即可。

1.2 有效试验条件的确定

为确定有效的试验条件，对不同条件的检测问题，建立了数值计算模型，利用上述有限元程序对检测信号进行了计算。

所建立数值计算模型如图3所示，主要参数为板长200 mm，宽50 mm，厚10 mm，缺陷孔洞在板的中央，缺陷直径分别为30，24，18，12，6 mm。

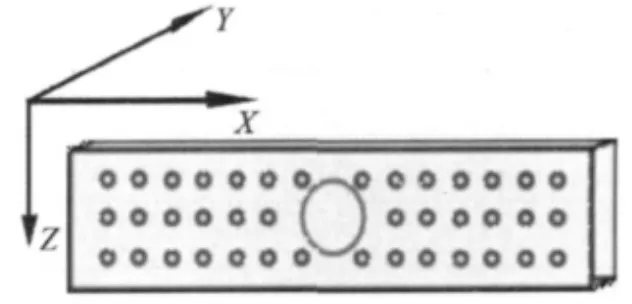
考虑到泡沫金属材料的特点，计算模型中用比致密金属材料电导率小的均匀材料来模拟泡沫金属[8]。

1.2.1 加载方式的影响

针对三种典型加载方式（侧面中心加载、上表面对边中点加载和体对顶点加载），用有限元程序计算所得上表面电位差分布如图4所示。其中所加恒定电流大小均为4 A。

可见，三种加载方式的结果在缺陷处电位差有一个峰值，可由此检测泡沫金属的内部缺陷。这些结果初步证明DCPD法对泡沫金属缺陷检测的有效性。

加载方式2和3的电极位置在上表面（检测面），电极的影响使其附近电位差值较大，不宜识别。因此采用方式1加载。

1.2.2 加载电流的影响

图5为采用加载方式1（侧面中心加载），分别施加4和10 A激励电流时，计算所得上表面中线上相邻点电位差。

计算结果表明，电流较大时缺陷信号增大，更易检出缺陷。结合试验中恒流源及纳伏表仪器检测范围，决定采用10 A的激励电流进行直流电位法检测试验。

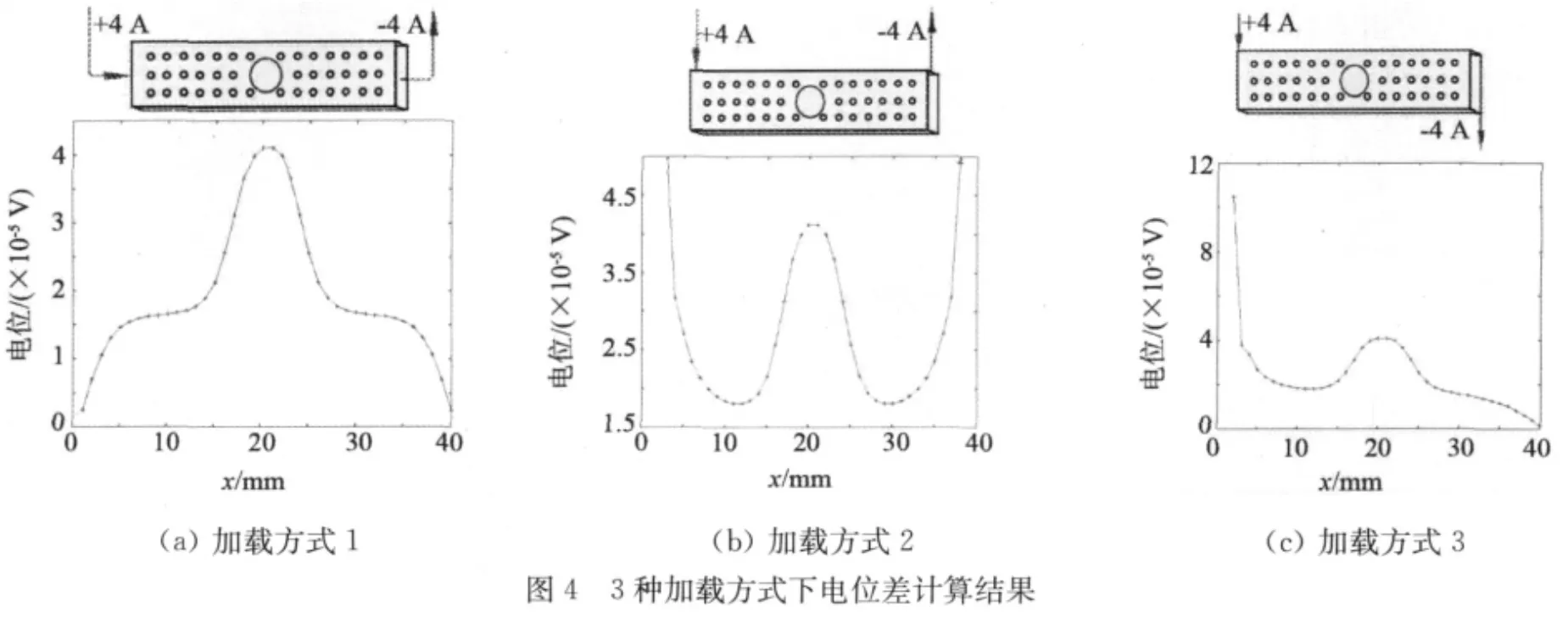
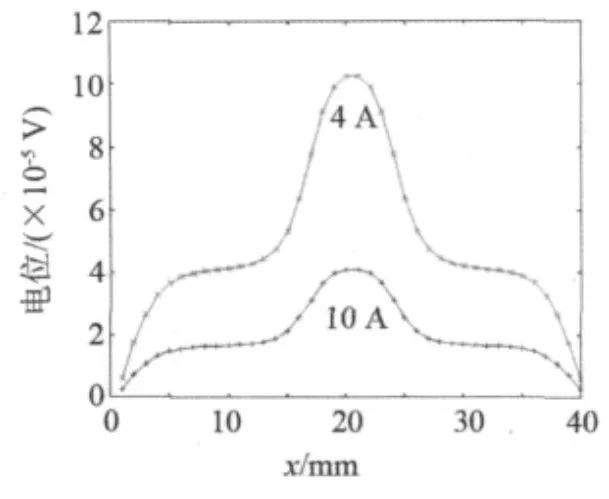
图5 电流为4和10 A时上表面电位

1.2.3 不同缺陷大小模型的电位差分布

对图3所示模型，不同直径缺陷产生的电位差信号如图6所示。计算中采用了侧面中心加载方式，加载电流为10 A。

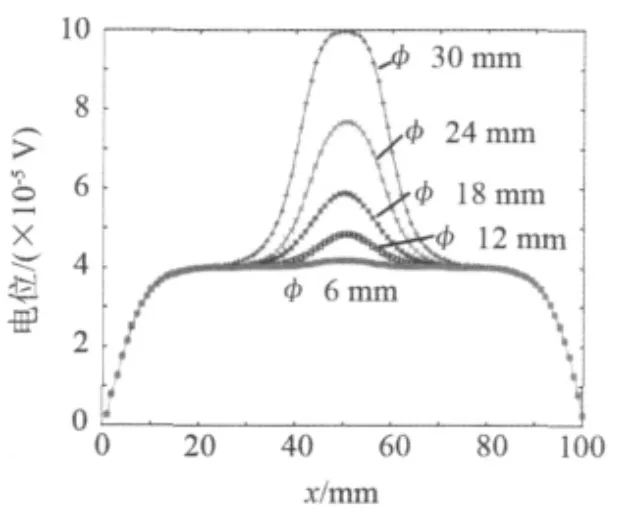
图6 不同缺陷大小的电位差

可见，当缺陷孔洞位置都在中心、孔洞大小不同时，检测信号的峰值位置相同，但峰值大小随缺陷孔洞的增大而有规律地增大。因此可通过信号的峰值来推定缺陷的大小。

2 试验

2.1 直流电位法试验平台的搭建

试验系统由直流电源（Agilent N6700B）、纳伏表（Agilent 71/2 Nano Volt/Micro Ohm Meter HP34401 A）、限流电阻（3个1Ω，50 W电阻并联）、三维扫查台（日本中央精机CHUO SEIKI 2轴控制器驱动QT－CM2）、试件、电位测量探针、电极及相应的夹具构成，系统结构如图7所示。直流电源、试件和限流电阻通过导线形成回路。

直流电源用来给试件加载恒流电流，从电源接出的两个电极夹在试件上；扫描台由步进电机精确控制，可由PC1上的Q－Edit软件进行编程控制；纳伏表测量试件检测表面的电位分布，探针在扫描台的控制下以一定的步长移动，每移动到下一点停止运动，将此刻测得的两探针间的电位差信号送入纳伏表；PC2与纳伏表连接，采集记录纳伏表测得的电位差。搭建的试验平台如图8所示。

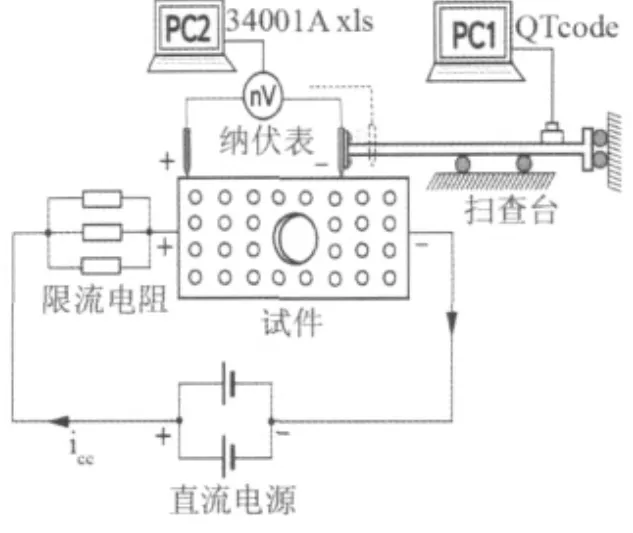
图7 试验系统结构图

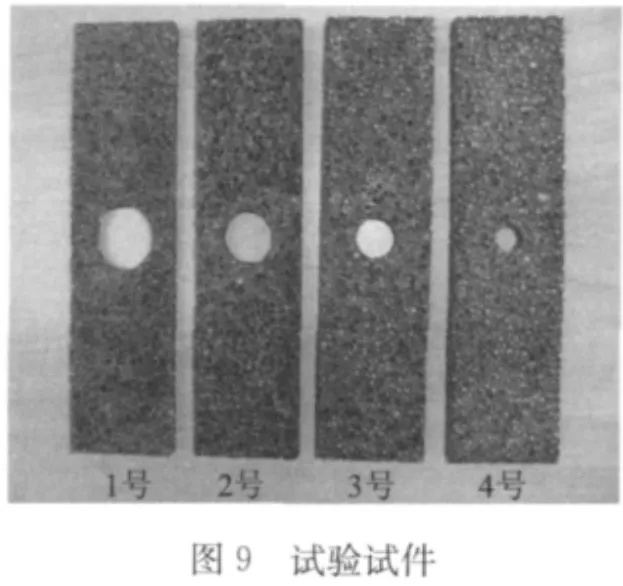
设计制作的具有不同大小缺陷的试件如图9所示。试件尺寸和数值计算模型相同。

2.2 泡沫金属直流电位法检测试验

在搭建的试验平台对上述试件进行直流电位法检测试验（图10）。具体试验条件为：恒定电流10 A；加载方式为侧面中心加载；纳伏表探针一端固定，另一端在扫描台控制下扫描。

图11 电位差分信号滤波结果

为了观察检测面电位差的分布，对试验测得电位信号相邻两点进行差分，并且对差分信号进行滤波处理以提高信噪比。所得上表面的电位差分布结果如图11所示。

可以看到，在缺陷位置有明显电位差峰值。1，2，3号试件中的缺陷从测量结果中可以分辨出，但4号试件信号很小，较难分辨。3号试件缺陷直径为18 mm，即宽度方向大孔缺陷检测能力在36%以上。

由于泡沫金属的电导率很大，电位差信号很小，这就对测量仪器的精度提出了很高的要求。泡沫金属材料本身不规则的小孔以及检测面的不平也给结果造成了明显的噪声。纳伏表的理论精度为1 n V，但实际测量时存在漂移，这对试验测量结果的精度有一定的影响。如果增大恒流源的电流值，检测出的电位值也会增大，这对减小噪声的影响有一定的作用。采用稳定性更好的纳伏表和更大的激励电流，会进一步有效增加本方法的检测能力。

3 结论

对实物泡沫金属进行了直流电位法无损检测试验，运用有限元分析程序对试验条件进行了选择。试验和数值结果显示，即使对于实物泡沫金属，也可以利用直流电位方法检出缺陷，且缺陷大小和检测电位信号的大小有一定对应关系。所得结果为泡沫金属的定量无损检测打下了基础。

[1]卢天健，何德坪，陈常青，等.超轻多孔金属材料的多功能特性及应用[J].力学进展，2006，36（4）：517－518.

[2]李家伟，陈积懋.无损检测手册[M].北京：机械工业出版社，2002：2－4；426.

[3]Tada N，Naoya.Application of direct－current potential difference method to evaluation of various damages in conductive materials[C].ASME 2008 Pressure Vessel and Piping Conference.USA：Chicago，2008.

[4]Tada N，Hayashi Y.Analysis on the applicability of direct current electrical potential method to the detection of damage by multiple s mall inter nal cracks[J].Inter national Journal of Fracture，1997，85（1）：1－9.

[5]Ghajar R.An alternative method for crack interaction in NDE of multiple cracks by means of potential drop technique[J].NDT＆E International，2004，37（7）：539－544.

[6]解社娟.泡沫金属无损检测方法研究[D].西安：西安交通大学，2009.

[7]盛剑霓.工程电磁场数值分析[M].西安：西安交通大学出版社，1999.

[8]刘培生，李铁藩.泡沫金属电阻率的计算方法[J].稀有金属材料与工程，1999，28（4）：19.