游戏算法分析在C语言教学中的应用

刘天时 李皎 陈明晰 西安石油大学计算机学院 710065

1 引言

算法是程序设计和软件开发的基础，也是计算机程序设计语言中一个重点和难点。算法具有不可见性、抽象性、复杂性是影响学生理解算法思想的重要因素[1,2]。由于其逻辑性强、实践性强，对初学者来说具有一定难度。因此，激发学生对算法设计的兴趣尤为重要。本文通过一些游戏案例来讲解算法设计思想，将学生对玩游戏的兴趣往设计算法的方向引导，从而促进学生理解一些典型算法设计思想。游戏算法分析教学方法使得学生从枯燥无味的算法学习中解脱出来，特别是学生一提到游戏，兴趣高涨，产生强烈的求知欲望，从而大大提高学生的学习兴趣，真正使学生爱学、乐学，达到寓教于乐的目的[3]。

下面以游戏案例为切入点，叙述程序设计中一些典型的常用算法，包括递归法、递推法和逆向法。

2 递归法

在算法分析与设计中，常常用到递归法。递归是指在定义自身的同时又出现了对自身的调用。递归方法可以把复杂问题逐层分解，最后将其划分为规模较小的问题进行解决，然后再逐层返回。使用递归方法往往使函数的定义或算法的描述简洁而且易于理解[4,5,6]。

汉诺塔问题是一个用递归思想解题的经典例子。汉诺塔问题可描述为：有3个分别命名为A、B、C的塔座，在塔座A上插有N个大小各不相同、从小到大编号为1，2，…，N的圆盘，且圆盘必须按照自下而上，由大到小叠放（如图1）。要求将塔座A上的N个圆盘借助塔座C移至塔座B上，并仍然按同样顺序叠放，圆盘移动时必须遵循如下规则：每次只能移动一个圆盘；任何时刻都不能将一个较大的圆盘压在较小的圆盘之上；在满足上述规则的基础上，圆盘可以插在A、B和C中的任一塔座上[4]。

可用递归思想分析该问题，当N=1时，只需将编号为1的圆盘从塔座A直接移至塔座B，不需要使用辅助塔座C，问题比较简单。当N＞1时，需要使用辅助塔座C，可先将N-1个较小的圆盘按照移动规则从塔座A移至塔座C，然后将剩下的编号为N的最大的圆盘移至B，最后再将N-1个圆盘按照移动规则从塔座C移至塔座B。这样，N个圆盘的移动问题可以转化为N-1个圆盘的移动问题。用函数Hanoi（N，A，B，C）实现将塔座A上的N个圆盘（如图1所示）按照移动规则借助塔座C移到塔座B上，最终圆盘必须按照自下而上，由大到小的方式叠放在塔座B上。用函数Move（N，A，B）实现将塔座A上编号为N的圆盘移至塔座B上。汉诺塔问题的求解算法如下：

用F[N]表示将N个圆盘按移动规则从塔座A移至塔座B至少需要移动的次数，由上述分析过程可知，F[N]=2F[N-1]+1，又因为F[1]=1，由以上两个等式可以推出F[N]=2N－1。

3 递推法

递推法是利用问题本身所具有的一种递推关系求问题解的方法。在教学过程中，可用兔子繁殖问题的例子引出一个具有递推关系的数列，即Fibonacci数列。兔子繁殖问题描述如下：兔子在出生两个月后，具有繁殖能力，一对兔子每个月能生出一对小兔子来。那么由一对小兔子开始，一年后可繁殖多少对兔子?

图2为兔子繁殖问题示意图，○表示一对小兔子，●表示一对大兔子，实线表示一对小兔子长大成为一对大兔子或表示一对大兔子照样生长，虚线性表示一对大兔子生出一对小兔子[7]。

由图2可知，一月份是一对小兔子，二月份这只兔子长成大兔子；三月份大兔子生出一对小兔子，此时共有两对兔子；四月份小兔子长成大兔子，大兔子又生出一对小兔子，此时共有三对兔子；五月份两对大兔子生出两对小兔子，小兔子长成大兔子，此时共有五对兔子。通过树形示意图观察，我们发现本月兔子等于上月兔子加上上月兔子。用F(n)表示第n个月底兔子的对数。

图1 汉诺塔问题初始状态

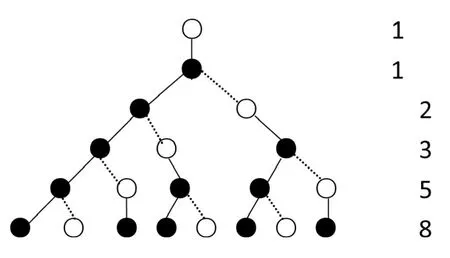
图2 兔子繁殖问题示意图

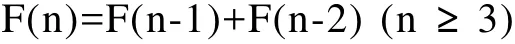
根据上面的递推公式，可以计算出从第一个月起，逐月的兔子对数依次是：1，1，2，3，5，8，13，21，34，55，89，144，233等等。这就是著名的斐波那契数列。

4 逆向法

数字拼图游戏，就是借助N×N矩阵中的空白单元，通过若干次移动空白单元格，把错乱的数字单元位置关系按先行后列的顺序，从小到大依次排列在N×N矩阵单元格中。把数字单元按照先行后列，从小到大排列，并且空白单元出现在N×N矩阵最后一个单元格的完成界面称为N×N数字拼图目的界面。数字拼图游戏的关键在于出题算法设计，即给出一个N×N错乱的数字界面。如何保证所出的游戏题有解，我们想到逆向法，即将游戏的目的界面作为逆向法的初始界面，从目的界面开始随机地移动一些步数，再把这个界面作为游戏的初始界面，这样可以保证每一个初始界面都是可解的[4]。

游戏中唯一的空白单元通常情况下可以向四个方向移动（特殊情况，空白单元与边相邻则可以向三个方向移动，空白单元与角相邻则可以向两个方向移动）。用数字1，2，3，4分别表示四个移动方向，即向上、向下、向左、向右移动。我们可以抽取1～4的随机数可以确定空白单元下一步的移动方向，通过记录每次抽取的随机数，便可知空白单元的移动轨迹。另一种记录游戏轨迹的方法是记录非空白单元的移动轨迹[4]。

对于N×N规模的数字拼图游戏，数字拼图出题算法如下：

Step3 若 K = 10N3，算法结束，否则转向Step2。

数字拼图出题算法可保证所出的题目有解，但是在出题中可能出现直接或间接重复移动，例如将同一个数字单元连续移动多次，或转圈循环移动等。可采用一些优化算法对简单的重复移动进行消除。例如，对“田”字型重复移动可消除，以简化移动轨迹。

另外，在算法教学过程中，我们应该注重以下几个方面的问题：（1）挖掘丰富游戏素材，激发学习兴趣；（2）某种类型的算法设计思想必须讲透，采用精讲多练的原则，不能过于宽泛；（3）应该配合具体游戏制作多媒体课件，通过图像、动画、影像、声音等多媒体信息使算法思想的讲解更为生动形象。

5 结束语

游戏案例分析教学以轻松愉快的方式让学生在娱乐中培养和锻炼学生的思维能力，是一种特殊的教学方式。与传统的教学方法相比,游戏案例分析教学使得算法教学具体、生动、形象，弥补了传统方法的不足。经过近两年在本校C语言课程教学中应用表明，该教学方法能消除学生对算法思想的神秘感和畏难情绪，激发了学生主动学习兴趣，使学生对于复杂、抽象的算法有一感性直观的认识和理解，提高了学生分析问题和解决问题的能力，取得了良好的教学效果。

[1] 郑宗汉，郑晓明.算法设计与分析[M].北京：清华大学出版社.2005.

[2] 崔彩峰，孙劲光.C语言程序设计教学方法的研究[J].中国科技信息.2009(09): 212.

[3] 李晓红.实施快乐教学提高教学效率之浅见[J].中国科技信息.2009(10): 258.

[4] 刘天时.软件案例分析[M].北京：清华大学出版社.2008.

[5] 唐自立.数据结构课程中递归算法教学探讨[J].中国科技信息.2006(8): 290-291.

[6] 谭浩强.C程序设计(第三版)[M].北京：清华大学出版社.2005.

[7] 黄忠裕.一个数学历史名题的模型建立及其教学设想——谈“兔子繁殖问题”[J].湖州师范学院学报.2003(03): 117-120.