一类非线性偏微分方程组的近似解法初探

赵小山，靳文娟，王 璟

（天津职业技术师范大学 理学院，天津 300222）

随着科学技术的发展，非线性科学在自然科学、社会科学领域中的应用越来越广泛，特别是寻找非线性发展方程的精确解在非线性的问题研究中占有重要地位。传统的求解非线性波方程的方法主要有逆散射法[1]、Bucklund 法[2]、Darboux 变换法[3]、Hirota 双线性法[4]和Painlevé展开法[5]等。近年来，涌现出一系列新的求解方法，如齐次平衡法[6]、双曲正切函数展开法[7]、EXP函数法[8]和变分迭代法[9-11]等。本文利用何吉欢教授[9]提出的变分迭代理论，对一类非线性偏微分方程组进行求解，得到了方程的近似解，同时证明了该解法的快速收敛性。

1 方法简述

本节主要简述变分迭代法[8]的主要内容。这一理论是对Inokuti提出的广义拉氏乘子的改进。在变分迭代法中考虑微分方程：

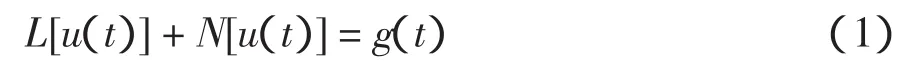
其中：L为线性算子；N为非线性算子；g（t）为非齐次项。用变分迭代法得式（1）的校正泛函：

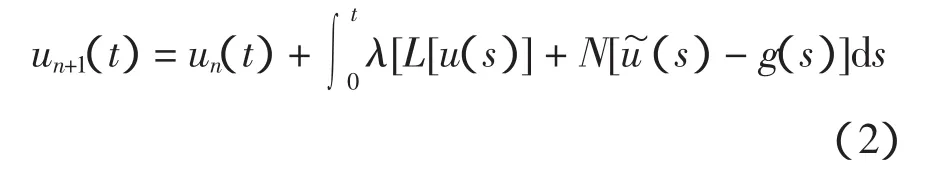
其中：λ为广义拉氏乘子；un为第n次近似解为限制变分，即n=0。

在该方法中，首先要确定拉氏乘子λ，λ可由变分理论识别。例如：所选乘子满足校正泛函取驻值，即δun+1（t）=0；再通过任意初始函数u0及计算所得的拉氏乘子λ得到连续逼近解un，n≥0。若连续近似解序列收敛，则可以得到精确解。

2 方法的应用

考虑如下方程组：

满足：u（x，0）=ex，v（x，0）=e-x。将式（3）转化为关于 u、v的变分形式，通过变分迭代法及式（2）对微分方程组（3）构建t方向的校正泛函，得：

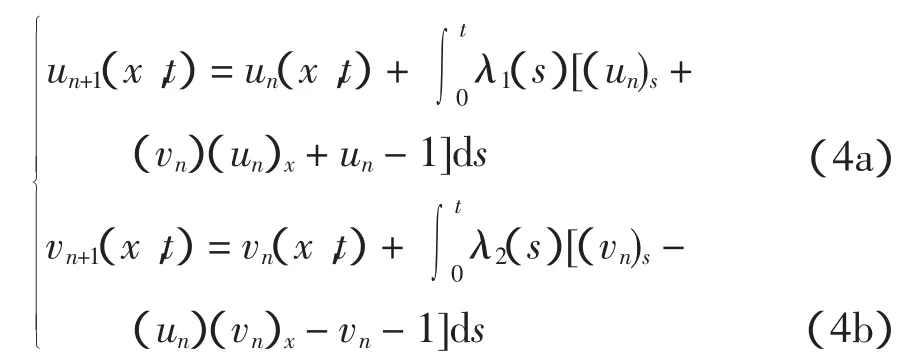
用变分理论中的限制变分的概念，将校正泛函式（4）重写：

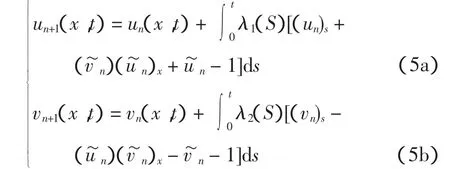
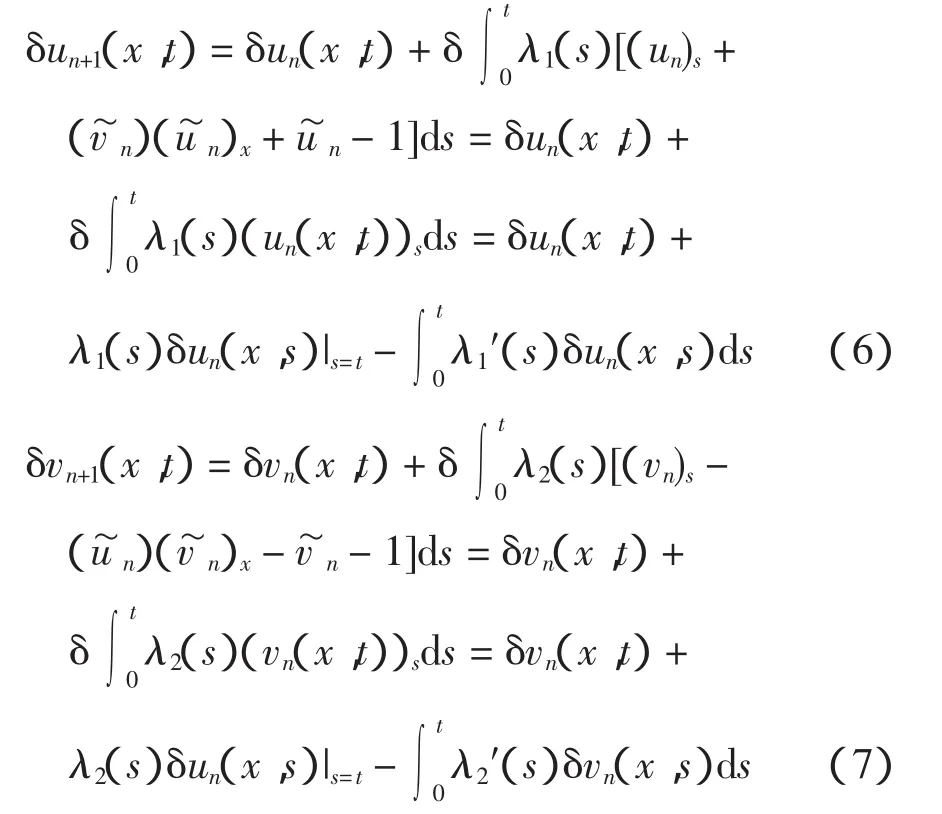
令δun+1（x，t）=0，δvn+1（x，t）=0，得：

由式（8）、式（9）求得拉氏乘子：

现将式（10）、式（11）分别代入校正泛函式（5），得下列迭代式：

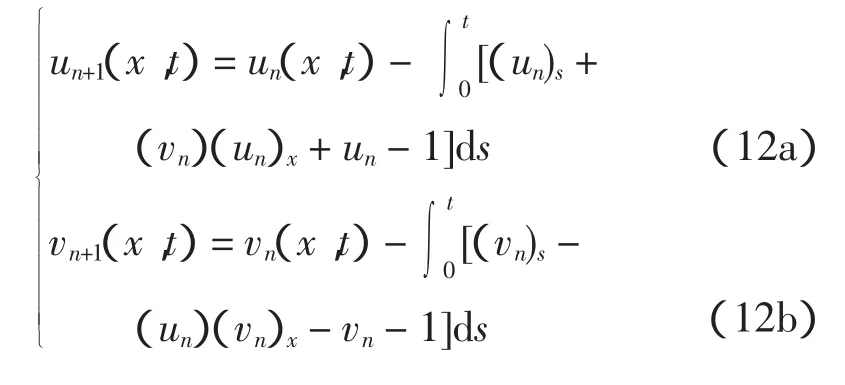
令u0（x，t）=u（x，0）=ex，v0（x，t）=v（x，0）=e-x，并将其带入式（12），得：

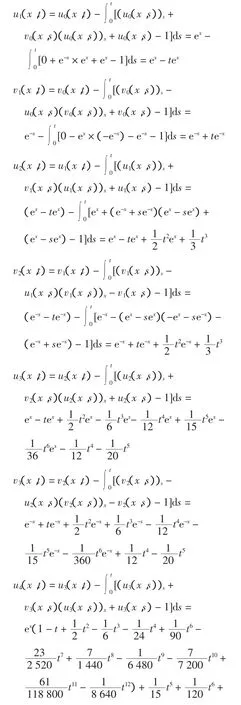
取定 t=0.1，x=0.5，得系统（3）精确解为：

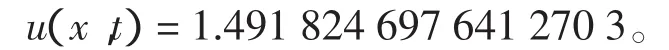
表1给出了各阶近似解的近似精度。

表1 系统（3）的近似解比较

由表1可以看出，每迭代一次，在确定其自变量取值后其精度不断提高，即近似值不断接近精确值，当迭代到第五次时已经很接近精确解。

3 结束语

本文通过采用变分迭代法，对非线性偏微分方程组进行求解，得到了二元非线性偏微分方程组的近似解，证明了变分迭代法求解非线性系统的有效性。

［1］ABLOW ITZ M J，CLARKSON P A.Soliton，Nonlinear Evolution Equations and Inverse Scattering[M].Cambridge：Cambridge Univ Press，1991.

［2］谷超豪.孤立子理论及其应用[M].杭州：浙江科技出版社，1990.

［3］MATVEEV V B，SALLEM A.Daroux Transformations and Solitons[M].Berlin：Springer，1991.

［4］HIROTA R.Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons[J].Phys Rev Lett，1971，27：1192-1194.

［5］楼森岳.推广的Painlevé展开及KdV方程的非标准截断解[J].物理学报，1998，47：1739-1745.

［6］WANG M L，ZHOU Y B.Application of homogeneous balance method to exact solutions of nonlinear equations in mathematical physics[J].Phys Lett A，1996，213：67-75.

［7］李志斌，张善卿.非线性波方程准确孤立波解的符号计算[J].数学物理学报，1997，17（1）：81-89.

［8］HE J H.New periodic solutions for nonlinear evolution equations using Exp-function method[J].Chaos Soliton Fract，2007（34）：1421-1429.

［9］HE J H.Some asymptotic methods for strongly nonlinear equations[J].Internat J Modern Phys B，2006，20（10）：1141-1199.

［10］ZHU J M，LU Z M，LIU Y U.Codoubly periodic wave solutions of Jaulient-Miodek equations using variational iteration method combined with Jacobianfunction method[J].Comun Theor Phys，2008（49）：1403-1406.

［11］CHEN X M，WANG L J.The variational iteration method for solving a neutral functional-differential equation with proportional delays[J].Computers and Mathematics with Applications，2010，59：2696-2702.