一种适用于水量传播特点的流量演算公式

潘文学,孙淑侠,雷智昌

(陕西水环境工程勘测设计研究院,陕西 西安 710018)

一种适用于水量传播特点的流量演算公式

潘文学,孙淑侠,雷智昌

(陕西水环境工程勘测设计研究院,陕西 西安 710018)

分析流量传播历时有多种方法,诸多方法都存在较大的误差。该文基于水文模拟观点,在马斯京根演算方程的基础上,对河道槽蓄量方程与河段水量平衡方程进行联解,并结合渭河中下游干流实测流量资料进行了流量传播演算。提出了适用于水量传播特点的流量演算公式以及流量演算经验参数,在此基础上推出由下断面流量反向推算上断面流量的反演概念性公式。演算结果表明,从林家村站流量到华县站流量,平均演算合格率在85%以上,远高于可行合格率70%,该方法精度较高,可供分析非汛期河流流量传播历时时参考。

流量传播;水量演算;马斯京根法

1 概 述

非汛期水量调度,其计算时段都大于各河段的流量传播历时。对这种情况,以往在大河流域水资源利用规划阶段常采用简化法处理:对短河段,下断面的流量直接采用上断面同时段的流量;对长河段,下断面的流量采用上断面前一时段的流量,即错后一个时段计算。

2 河段流达时间分析

河道水流流达时间(即流量传播历时)是水量演算的最基本的物理量水量[1]。流量传播历时的长短与河段长度、流量大小、河道形态、水力条件等因素有关,对于一定的河段,水流传播的边界条件一定,流达时间主要受流量的影响,是流量的函数。

分析流量传播历时有多种方法,如相应流量法、相同流量法、洪峰流量法等[2]。利用相同流量法分析流量传播时间,原理清晰,方法简单。但该方法要求计算河段断面规则,变化较小,或者说上、下断面要有代表性,如果计算河段断面变化很大,则上下断面的流速均值就难以代表整个河段的平均流速,其计算结果也就与实际偏离较大。其次,该方法基于等流量统计传播历时,要求河段流量变化平稳,但实际上河段中大多有水量加入或引出,尤其在小流量时,水量的加入或引出对计算结果影响就更大。

3 流量传播演算方法

3.1 演算公式的建立

以往对洪水流量的演算是从两种观点研究的,一是着眼于下断面的流量是如何组成的;二是着眼于上断面一个单位的水量或流量到达下断面时其时程是如何分配的。前者常用马斯京根法[3],后者常用汇流系数法[4]研究。

对河道内水量演算也可着眼于下断面的水量组成,据此有两种研究方法:一是相关分析法,统计分析下断面的流量与上断面不同时段流量的相关关系,建立上下断面流量相关关系式;二是水文模拟法,采用流量演算方程导出长时段流量演算公式。下面采用水文模拟法,利用马斯京根方程推导河道流量演算公式。

马斯京根法是由Macoarthy在1938年提出并在30年代首先应用于美国马斯京根河的一种方法,该方法认为在一个河段中,河道槽蓄量W与某一“特征流量”Q′之间存在线性关系 ,即:

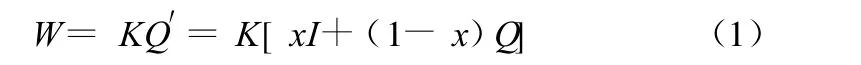
该公式与河段水量平衡方程:

式中:I1、I2为上断面时段初、末流量;It、It-1为上断面本时段、上时段流量;Q1、Q2为下断面时段初、末流量;Qt、Qt-1为下断面本时段、上时段流量;K、x为河段水力、水文特征参数,K称为槽蓄系数,x称为权重因子。

由式(1)～(4)可得:

上式表明,K、x与C0、C1、Δt有关,而与C2无关。可以证明,当上游无流量注入时,C2是流量消退系数,即:

在用马斯京根法对河段洪水流量演算时[5],为使流量在Δt时间及沿河长的变化都接近于线性,Δt取值应 ≤K,河段短时取 Δt=K,河段太长时,应分段演算。

对河道内流量演算,由于流量的传播呈模糊,K、x更是概念模糊,因而,在流量演算中K、x已演变为一种水量演算系数。基于这种观点,可把马斯京根公式作为一种水文模拟公式,并进行如下推导:

如果K＜＜Δt,则Qt≈It,即河段很短时下断面流量等于上断面流量。

如果K=Δt,则有Qt=It-1,即河段很长时下断面流量等于上断面前一时段流量。

通过上述推导分析可知:

河段很短时,即当K＜＜Δt时,有Qt≈It,这是在C1=0,C2=0的条件下推导的结果,表明河段蓄水消退很快及C0=1时,本时段下断面流量可移用本时段上断面流量。

从实用角度,在 Δt＞K的情况下,本研究推荐式(15)、(16)为河道流量演算公式,即:

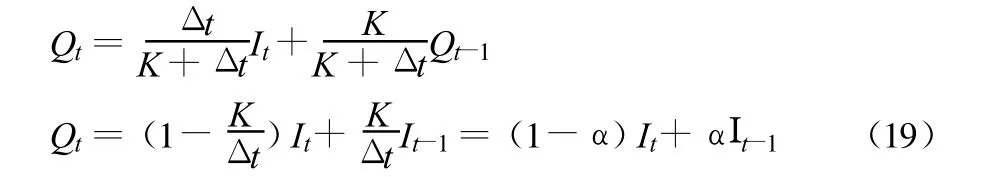
公式(19)为流量平衡方程。由以上推导可以证明,该式可以用于河段内流量的传播演算。

3.2 区间入流及引水的处理

上述流量演算方程是在河段内无其它加入和支出项时推导的,当区段有入流和用水时,应将区间入流和用水作为平衡项考虑其影响。设QR表示区间入流,QY表示区间用水,通过实测资料演算,认为可按以下方法考虑:

(1)当区间入流与区间用水之差(QR-QY)小于下断面流量5%时,可忽略不计,仍按公式(19)演算;

(2)当(QR-QY)占到下断面流量5%～15%时,可按下式演算:

在(20)式中,(QR-QY)项没有考虑传播问题,只是作为下断面节点流量平衡项直接加入,究竟是否需要考虑传播时间,在具体操作时可根据各河段主要取水口、入水口位置按以下原则考虑:如果主要取水口或入水口位置在靠近上断面的1/5河段长范围内,可将其并入上断面流量中一同考虑传播问题;当在1/5～3/5范围内时,可将其单独演算至下断面;当在靠近下断面2/5河段长范围内时可不考虑传播问题,直接按(15)式演算。

(3)当(QR-QY)占到下断面流量的15%以上时,可按有大支流加入进行演算:

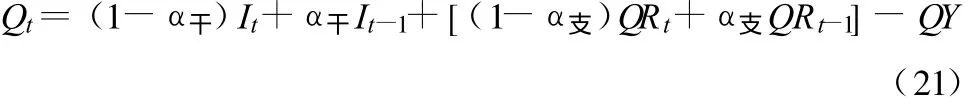
3.3 演算参数α的确定

3.3.1 单一河段K、α的确定

有3种方法,一是根据马斯京根方程[6]W=KQ′=K[xI+(1-x)Q]为线性的原则,利用河段内无区间入流及引水的实测流量资料,用试错法确定x值,当选定的x使W～Q′关系线为直线时,W～Q′的斜率即为K值。二是采用设定流量相应的流速,计算 τ=0.278。三是优化法,根据河段多年实测资料,应用演算公式实际演算河道流量,以演算值与实测值误差最小或演算合格率最高(以误差小于等于20%为合格)为目标确定相应的K值。这3种方法一般联合使用,即以值为初始值,以优化法确定的值为最终采用值。

3.3.2 多河段演算参数K(i)的确定

由于河道的流量演算受到各河段的河道特性、水文、水力特性的影响,所以多河段的流量演算有别于单一河段,各河段的K将受制于多河段流量累计演算结果的约束。此时,各河段K的确定以最终断面的演算合格率最高为最好。一般认为合格率达到70%以上便认为K可行。

4 算 例

根据1990年～1999年资料,利用相同流量法分析计算渭河中下干流不同流量情况下的流量传播历时,其分析结果如表1。

表1 渭河北道～华县各河段不同流量的传播历时(h)

陕西省水文局根据20世纪90年代水文观测资料,结合经验判断,综合分析得出干流各河段流量传播时间,如表2。

从表1和2可以看出,虽然两个结果不完全相同,表1结果偏大,尤其是流量较小时两者相差更大,其原因就是区间支流加入的影响,在小流量阶段,支流加入相对影响较大,计算误差就大;而当河道流量增大时,支流加入的影响相对减小,计算误差也就减低。表2根据资料分析,结合经验判断,考虑支流加入及区间流量变化的影响对结果作了调整,比较符合实际。

表2 渭河干流各河段流量传播历时(h)

根据渭河林家村至华县各断面1980～1985年实测流量资料[7],进行河段流量演算,以检验上述方法的应用效果。演算结果如表3所示。

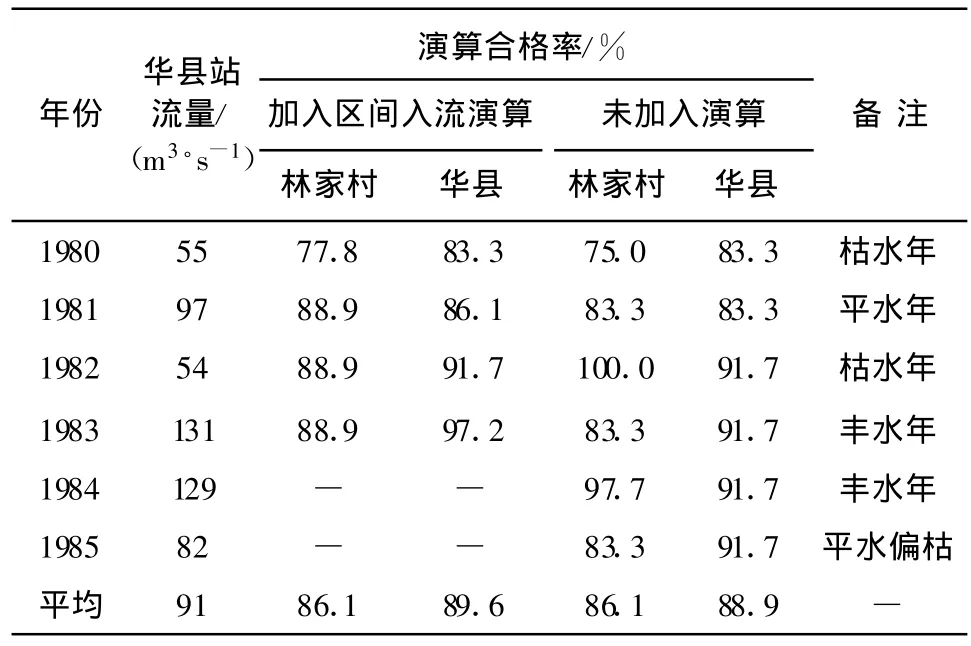
表3 演算结果统计表

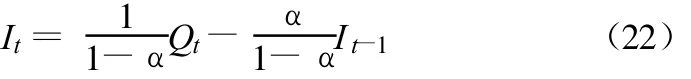
同样当有区间水量变化时,需将其作为平衡项加入上式:

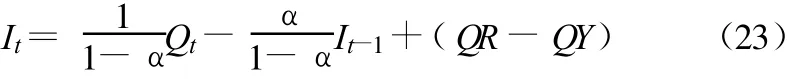
由表3可以看出,从林家村一直演算到华县,平均合格率达85%以上,证明所给系数取值可以应用。

上述方法是考虑流量传播因素时由上断面流量演算下断面流量的公式。在研究中,有时会遇到由下断面流量反推上断面流量的情况,此时可采用公式(18)的逆形式:

另外,还有一种情况就是由水库下游各河段时段缺水量推求水库最小补水量,这也是一个流量反演问题。过去大多采取错后一个时段计算的方法,但在具体应用上有不方便之处。因此,仿照公式(18),本文建议对此可采用如下概念性公式:

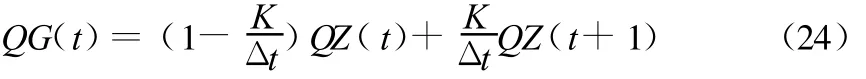
式中:QG(t)为水库t时段需补水量;QZ(t)、QZ(t+1)分别为第i河段本时段和下一时段缺水量。

5 结 语

本文基于水文模拟观点,在马斯京根演算方程的基础上,推导出了适用于流量传播特点的流量演进公式,提出了流量演算经验参数,并从理论上证明了公式的正确性。在此基础上还提出了由下断面流量反向推算上断面流量的反演公式。

流量传播是水量调度中需要解决的一个主要问题。以往对洪水流量的传播及演进研究较多,也有许多成熟的方法和公式,但在水量调度中,由于计算时段都大于河段流量传播时间,与洪水传播条件不同,目前研究很少,许多问题有待进一步研究。

[1]杨小柳.实时洪水预报方法综述[J].水文,1996,(4):9-16,65.

[2]林三益.水文预报[M].北京:中国水利水电出版社,2001.

[3]许拯民.马斯京根法应用研讨[J].华北水利水电学院学报,2005,26(4):1-3.

[4]朱华.水情自动测报系统[M].北京:水利电力出版社,1992.

[5]张大伟,董增川.Preissmann隐式格式在新沂河洪水演进中的应用研究[J].水利与建筑工程学报,2004,2(4):41-43.

[6]M.Perumal.Unification of Muskingum Difference Schemes[M].Journal of Hydraulic Engineering,1989.

[7]马雪妍.渭河下游河道横断面调整特点及原因简析[J].水利与建筑工程学报,2006,4(1):32-36.

Study on Flow Propagation and Calculation

PAN Wen-xue,SUN Shu-xia,LEI Zhi-chang
(Shaanxi Investigation&Design Institute of Water Environment Engineering,Xi'an,Shaanxi710018,China)

Most methods for analyzing the flow propagation have errors.Based on the hydrological modeling and Muskingum calculus equations,the water flow calculation formula applied to the dissemination characteristics and the experience parameters of run-off calculation are analyzed and proposed here.On this basis,the inversion formula for calculating the upsection flow from the next section flow is put forward.The successful application of the formula in calculating the flow propagation for middle reaches of Weihe River shows that the theory and method are all feasible and reasonable.

flow propagation;water calculation;Muskingum method

P333.1

A

1672—1144(2010)02—0023—04

2009-12-28

2010-01-17

河南省软科学研究(0613032000)

潘文学(1977—),男(汉族),陕西韩城人,硕士,工程师,主要从事水文设计与水资源系统研究。