多传感器信息融合的分层着色Petri网模型
2010-07-18侯平智
吴 锋,侯平智
(杭州电子科技大学信息与控制研究所,浙江杭州310018)
0 引 言
高技术条件下的现代战争越来越表现出高强度、快速、精确的特征,这对信息融合系统提出了更高的要求。近20年来,人们对信息融合及其系统的研究取得了显著的成果,使其逐渐成为一个独立的研究领域。尽管如此,仍缺少一个描述信息融合系统的形式化框架,通过形式化的方法定义、分析、验证,最终设计信息融合系统。多传感器信息融合过程是典型的离散系统,对离散系统进行建模的常用方法有:UML方法、IDEF方法、Petri网方法、基于活动的随机网络方法等[1]。Petri网是一种可用图形表示的组合模型,具有直观、易懂和易用的优点,对描述和分析有独到优越之处。同时,Petri网又是严格定义的数学对象,借助于数学开发的Petri网分析方法和技术既可用于静态的结构分析,又可用于动态和行为分析,具有灵活的建模和强大的系统性能分析能力[2-4]。基于Petri网的建模技术可用于模拟带有并发性、异步性、分布式、非确定性、并行性等特性的系统,已成为目前最有前途的建模工具,越来越多的应用领域采用它来进行系统评估[5-7]。本文利用分层着色Petri网(简称HCPN)在系统建模领域的优势,从系统顶层设计的角度出发,对多传感器信息融合过程进行建模,以便于融合系统的性能分析和行为仿真。
1 分层着色Petri网概述
普通Petri网出现了两个严重不足:一是无数据概念;二是无层次概念。这些限制使之只能进行小系统的建模。HCPN赋予令牌颜色和具有层次网络的特点,有机地结合了数据结构和层次分解,可对各种大型复杂系统进行建模和仿真,如复杂制造系统、社会经济系统、大型军事系统等,从而验证系统逻辑的正确性和评估系统的性能。HCPN既有直观形象的图形表示又有强大的数学理论支撑,提供了公式化的验证方法,如状态空间分析和不变量的分析方法。下面在简要介绍HCPN原理的基础上,以文献2中的空对空导弹攻击系统为例说明多传感器信息融合系统的建模与分析方法。
1.1 着色Petri网
着色Petri网的定义可以用一个六元组合(P,T,C,I,O,M0)表示[1-4],其中:
(1)P和T分别是库所和变迁的非空有限集,满足P∩T=Φ,P∪T≠Φ;
(2)色彩集C={C(P),C(T)},C(P)是每个库所的色彩集,C(T)是每个变迁的色彩集;
(3)着色库所集P={
(4)M0为初始令牌集。
变迁规则定义如下:
(1)在标识M下变迁tj关于色彩bjk使能,当且仅当∀pi∈tj,M(aih)≥I(aihbjk)时,使能的变迁激发后,将产生新的标识M′;
(2)M′的确定算法为∀pi∈tj,M′(aih)≥M(aih)+O(aihbjk)-I(aihbjk),否则M′(aih)=M(aih)。
1.2 分层着色Petri网模型
HCPN能对大型复杂系统进行建模主要在于其两个重要特性:一是标记的颜色可以是任意复杂的数据,大大简化了网络的复杂度;二是具有层次结构,这可以从整体到局部、由粗到精地把系统分页,进步细化,突出重点。
在分析业务流程中,有些任务是不可分的或者说是可以直接执行的,称为原子任务。而有些任务是可进一步划分的,称为复合任务,它实际上也是一个业务过程。同理,复合任务中还可以含有复合任务。相应地,在Petri网描述中,将变迁分为两种:基本变迁和子网变迁。基本变迁表示原子任务,子网变迁表示复合任务,它有其内部结构、内部行为和内部状态。Petri网的多层化建模隐藏了子网内部结构,在建模时集中于相应的抽象层次,使业务流程模型具有良好的结构,便于对其分析处理。
2 问题描述与建模
2.1 问题的提出
HCPN模型适合描述复杂的军事系统,采用HCPN模型来模拟导弹攻击目标,以验证导弹的控制与引导功能。如图1所示的空对空导弹攻击系统中[2],当攻击机发现目标后,就发射空对空导弹。发射之后,导弹利用自己的引导系统跟踪目标。导弹有两套侦察机制:雷达和红外传感器。这些物理设备用于检测目标的位置,提高命中精度。例如,由于目标干扰等造成雷连测量数据有误时,将使用红外数据,并进行数据融台;之后引导装置计算导弹拦截目标的弹道轨迹,由控制算法来控制导弹的推进器。将要模拟的就是雷达和红外传感器的信息融合、导弹跟踪、指挥决策并击中目标的过程。
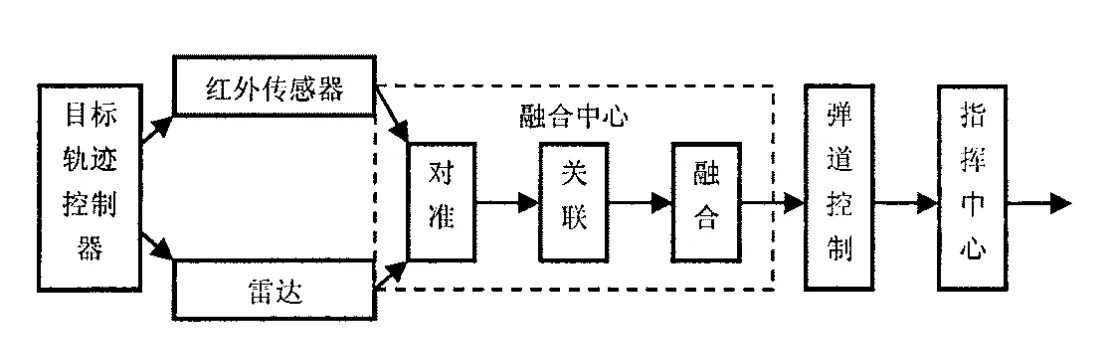
图1 空对空导弹攻击系统
2.2 Petri网建模
根据图1的空对空导弹攻击系统,确定该物理系统由6部分构成:目标、雷达、红外传感器、融合中心、弹道控制和指挥中心。建立的HCPN模型如图2所示,其中目标t1、指挥中心t6可进一步细化为目标子网如图3所示,和指挥中心子网(假如指挥中心由三人组成)如图4所示,相应的变迁如表1-3所示。令牌颜色定义为:颜色/状态(准备就绪,等待),颜色/目标(目标改变,停止),颜色/运动(目标轨迹,导弹轨迹),颜色/范围(红外范围,雷达范围)。

图2 空对空导弹攻击系统的HCPN
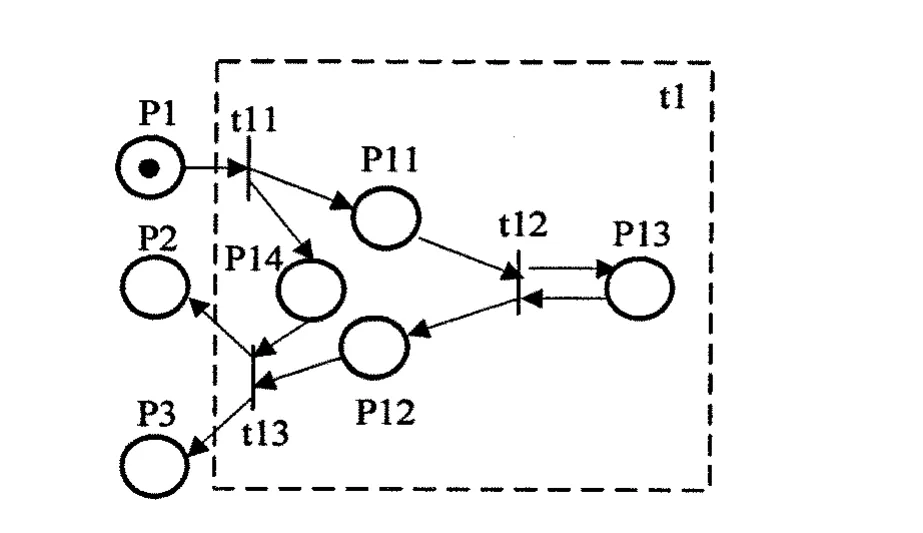
图3 目标子网
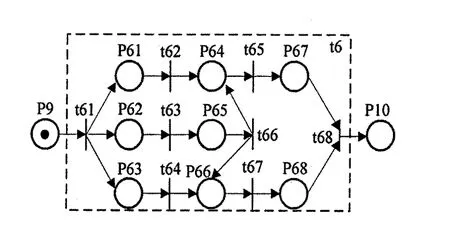
图4 指挥中心子网
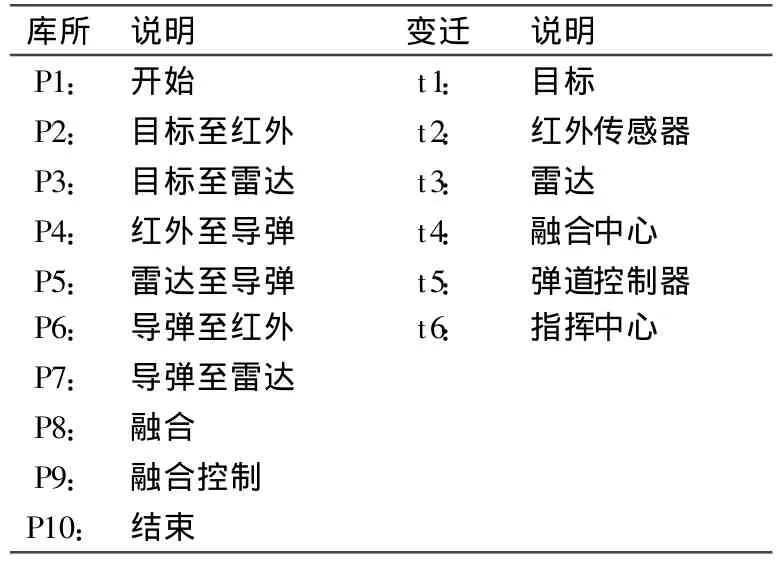
表1 空对空导弹攻击系统的库所与变迁
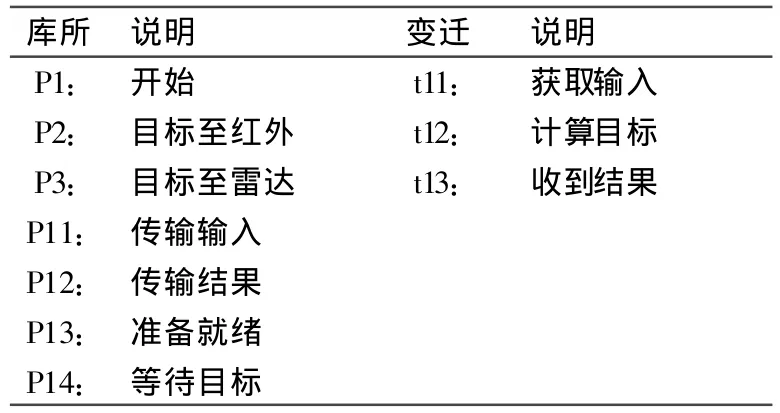
表2 目标子网的库所与变迁
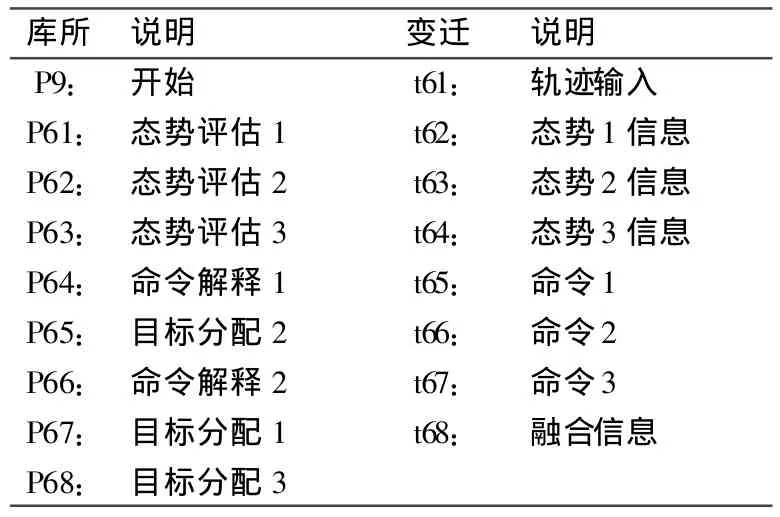
表3 指挥中心子网的库所与变迁
3 融合算法分析
3.1 融合中心的数据融合算法
在图2中的融合中心进行数据融合时,应先将多传感器数据做时间对齐、坐标统一和数据关联等处理[5,6]。多个传感器往往分布在不同的地域,在进行多个传感器融台时,需将各传感器的数据换算到一个坐标系及同一时间才能进行融台,这将使融合算式变成非线性微分方程,不能直接求解。文献6提出一种直接解析求解的方法,它不是求解非线性微分方程,而是将各传感器直接观测量换算到状态坐标系,并换算(外推或内插)到同一时间,得到新的观测线性方程:

式中,Vi为新的观测误差。设原观测矢量YM=[γ α ε],γ、α及ε分别为传感器观测目标的距离、方位及仰角等数据。新观测量可表示为:Y=[yxyyyz]T,Y(ti)与未知的状态量X(ti)属同一坐标系的相同坐标,利用正态分布最大似然准则或加权展小二乘准则,便可求出最优状态估计值Xˆ的解析解:

式中,R为新观测量Y(ti)的误差Vi的均方差向量。当N传感器报来N个观测量时,展开式2:

式中,i指第i个传感器报来的观测数据及均方差的号码,N为能同时观测目标的传感器的数量。和ˆz的表达式与ˆx类似,有关融合算式3的进一步细节见文献6。
3.2 指挥中心的神经网络算法
在图4中的3人决策信息融合过程,经弹道控制计算出的导弹轨迹信息,经信息融合(IF)、态势评估(SA)、命令解释(CI)和目标分配(TD)后作出决策。决策融合是信息融合的高级阶段,在文献7的基础上使用人工神经网络融合算法可以表达基于演绎逻辑的推理过程。
考虑一个具有单隐层的3层BP神经网络如图5所示,其基本数学模型为:

式中,x、x′、y分别为输入层、隐含层和输出层矢量(节点向量);v、ω、θ1、θ2分别表示隐含层与输出层、输入层与隐含层之间连接权值和阀值;f(x)为网络激活函数
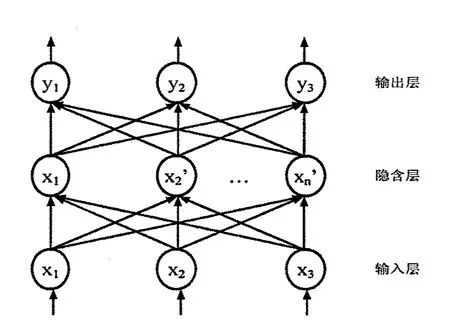
图5 单隐层的三层神经网络
3.3 仿真分析
使用CPN-tools仿真软件对Petri网模型进行仿真分析,可以观察位置中的标识变化情况,分析系统的性能包括死锁、可达性等特性。假设各传感器检测到目标的概率、跟踪器对数据处理的正确率、融合中心和指挥中心对数据的处理时间等,通过运用CPN-tools软件,可以知道该模型是有效的。
4 结束语
本文以空对空导弹攻击系统为例,提出了用分层着色Petri网描述多传感器信息融合系统的方法,并给出了Petri网主网模型和其中子网变迁的Petri子网模型。与普通Petri网相比,采用着色Petri网能够将系统中变迁发生的不同事件用不同的颜色来表示,可将系统中数据融合过程及指挥指挥中心的决策过程按照实战中的处理规则反映到模型上,进行模型分析和仿真验证。同时,有关数据融合算法为多传感器数据融台的解算效率提供了基础。
[1] 赵强,周林,陈维,等.基于分层着色Petri网的地空导弹装备维修建模[J].航空计算技术,2008,38(6):28-31.
[2] 肖兵,瞿坦,王明哲.着色Petri网及其在系统建模与仿真中的应用[J].计算机工程,2001,(1):30-32.
[3] 伍宏伟,杨东.基于赋时层次有色Petri网的医疗服务流程建模与优化[J].系统仿真学报,2007,19(8):1 657-1 663.
[4] 袁崇义.Petri网原理[M].北京:电子工业出版社,1998:51-73.
[5] 陈玉坤,司锡才,李志刚.雷达与红外传感器数据关联及融合算法研究[J].传感器与微系统,2007,26(3):37-39.
[6] 刘兴.多传感器数据融合的实现技术[J].电子学报,2001,29(9):1 240-1 242.
[7] 李赣湘,张端金.模糊Petri网与C3I信息融合[J].弹道学报,1997,9(4):15-18.
