基于垂直面阵水下定位的算法研究*

徐寿志,程鹏飞,蔡艳辉,李为乔

(1.辽宁工程技术大学,辽宁阜新 123000;2.中国测绘科学研究院,北京 100830)

0 引 言

在海洋开发、海洋工程及海军技术领域广泛使用各种水声定位跟踪系统来确定水下目标的位置及运动轨迹。按照测量基阵的基线尺度,尤其是相应的定位解算模型,把定位系统分为超短基线模式(USBL),短基线模式(SBL)和长基线模式(LBL)[1]。文献[2]通过水面上的浮标,利用差分GPS得到浮标位置,然后提出了基于水面长基线的双曲线定位模型对水下目标进行定位。文献[3]利用线阵和目标点的几何位置关系自定义平面坐标系,提出了基于线阵的超短基线水下定位的解析求解算法。通过比较分析得出最小二乘解优于解析求解。对于基线阵位于一个垂直面内时并没有给出具体的解算模型。通过在湖北清江的多目标水声信号识别与检测试验,提出了利用距离交汇短基线定位模型解算水下目标点三维坐标。当面阵上有四个信号接收器时,可以通过解析法求得目标的唯一解。当信号接收器多于4个时,利用最小二乘法可以求得目标的最优解。

1 面阵的水下定位原理

假定F为目标发射源,M 1,M 2,M 3,M4,M5和M6为信号接收器,信号接收器之间的距离如图1所示,通过卷尺进行量测。其中,要求接收器必须安装精密时钟,在接收到水下目标发射的信号后,通过示波器和信号处理技术可以求得各信号接收器接收的时刻。设目标F发射时刻为t0,接收器M1、M2、M 3、M4、M5、M 6分别记录水声信号到达时刻t1,t2,t3,t4,t5,t6。为了节约成本,目标F没有安装精密时钟,它仅是提供可被信号接收器识别和接收的信号。所以,已知条件是信号接收器之间的距离和各信号接收器的接收时刻,同时,水声声速通过声速剖面仪测量得到,即水声平均声速V也是已知的。未知参数为F的三维坐标和发射时刻。信号接收器等于4时可以通过解析法求得唯一解,大于4时,可用最小二乘获得最优解。

2 面阵的坐标解算

建立如图1所示的坐标系,M 4,M1为已知点,它们的坐标分别为(0,0,0),(0,0.8,0)。令L1=0.765 m,L 2=0.5 m,L3=0.82 m,L 4=0.53 m,L 5=0.75 m,L6=1.25 m。则通过 M4、M 1及L 1和L2交会可以计算M2的坐标;同理,还可分别算出M3,M 5,M 6的坐标。

如图2所示根据下面的公式可以算出各未知

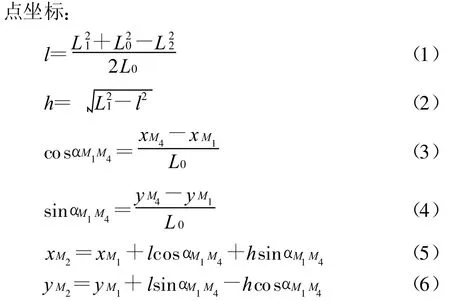
得到M 2,M3,M5,M6的坐标分别为(-0.462294,0.190484,0),(-0.513336,1.43944,0),(-0.00822776,1.59996,0),(-0.0149536,1.9999,0)。

3 面阵水下定位的距离交汇模型

距离交汇模型是间接测量水下目标到信号接收器的距离,通过信号接收器的接收时刻和信号发射器的发射时刻的时间差与水声平均声速的乘积求得。当水下目标发射信号时,经过一段时间后被信号接收器接收并记录其到达时刻[4]。由于目标的发射时刻是未知的,所以应通过增加信号接收器的个数。即增加观测方程的个数,然后对它们进行适当的变形就可以求出水下目标的三维坐标。其距离观测方程为

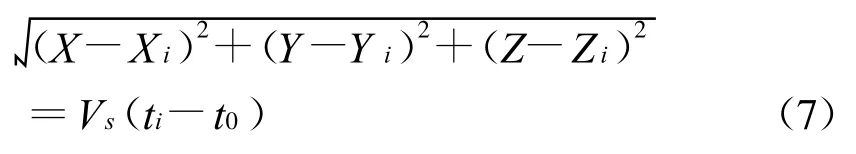
其中:X,Y,Z为水下目标点的坐标,X i,Yi,Zi为信号接收器的坐标,Vs=1469 m/s为水声的平均声速,ti为水声信号到达信号接收器的时刻,t0为水声信号水下目标的发射时刻。

3.1 解析求解

距离交汇模式的定位模型实际上是圆定位。当有四个信号接收器的观测数据时,采用解析表达式可直接求解水下目标的坐标,已知观测方程为

其中:Vs=1469 m/s。

将上述各式平方,式(9)、(10)、(11)分别与式(8)作差 ,得

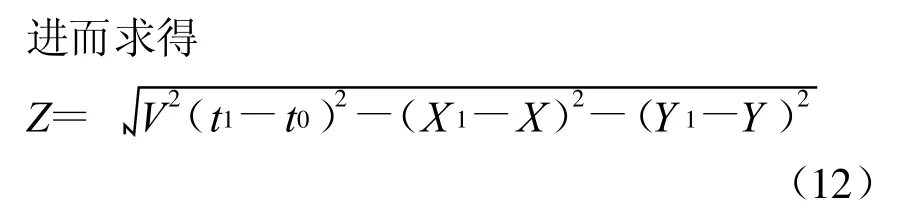
3.2 最小二乘求解

当信号接收机多于4个时,应采用最小二乘法求解水下目标的坐标。由于距离交汇定位是非线性定位,所以需要对非线性方程在目标点附近进行线性化,得到线性差分方程。因此,最小二乘法需要知道水下目标的近似坐标,可以从观测数据中挑选4个通过解析法求解近似坐标(X 0,Y 0,Z0)。根据已知条件可列出如下方程[5]

根据泰勒公式对F在(X 0,Y 0,Z0,ti,t0)处进行展开,得

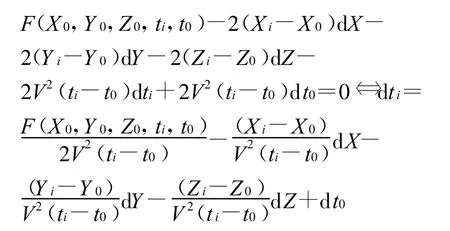
4 水下目标定位试验

本次试验是在湖北清江平洛湖上游进行的。试验当天气候较好,无风且船只少,因此,由坏境影响引起的观测误差相对较小。首先,根据实际要求连接好仪器。然后,把面阵近乎垂直放入水中,最后,按上信号发射器电源并放入水中。放入水中后信号发射器开始发射信号,接收面阵(含6只水听器),接收发射来的信号经信号调节器放大后用数据采集仪记录,输出到计算机,用MATLAB程序处理。试验原理如图3。

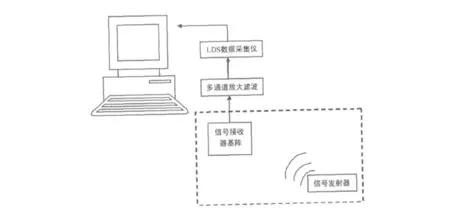
图3 试验原理图

数据处理过程如下:

首先,对接收信号检波取包络,若脉冲包络幅度超过检测门限且脉宽超过宽度门限,可能存在目标信号,记下脉冲前沿为信号到达时间,同时启动Notch滤波器加瞬时频率方差检测器(VIFD)进行识别及检测处理。各个信号接收器的接收时间如表1所示。定位结果如表2所示[6]。

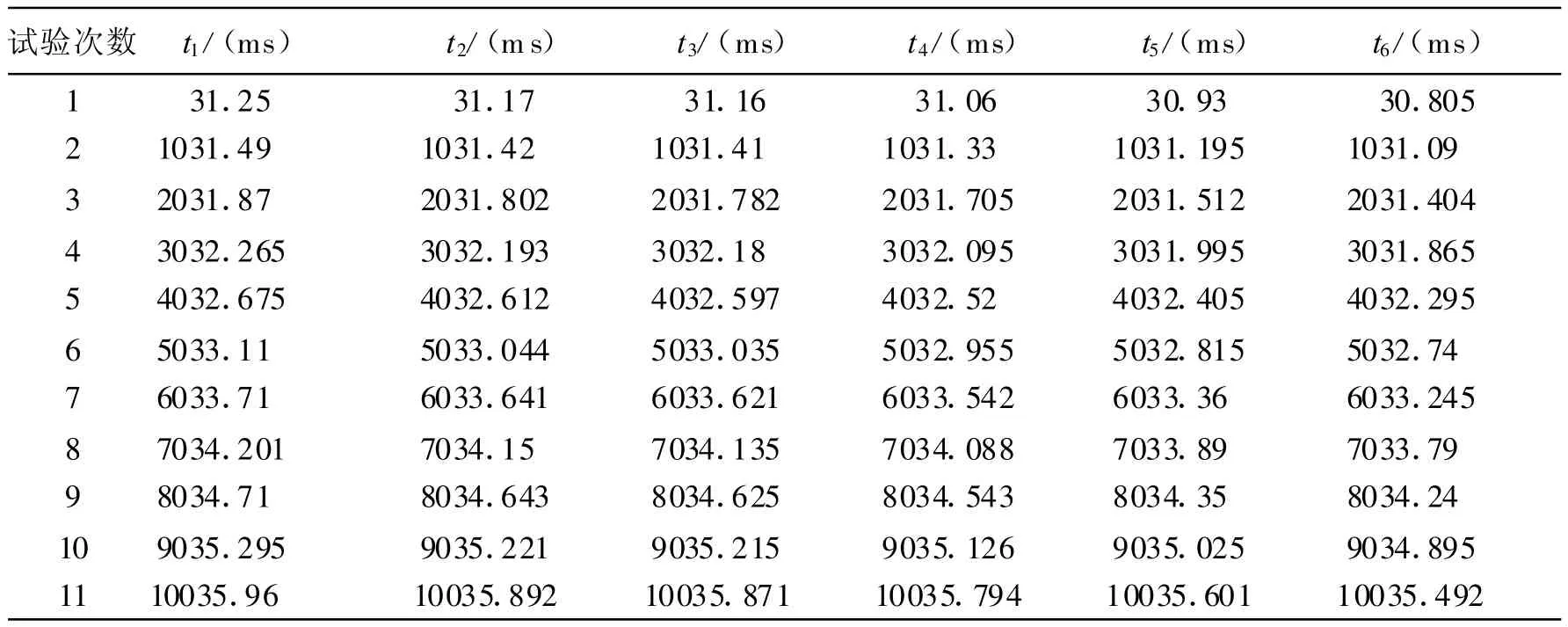
表1 信号接收器的接收时间

表2 试验的定位结果

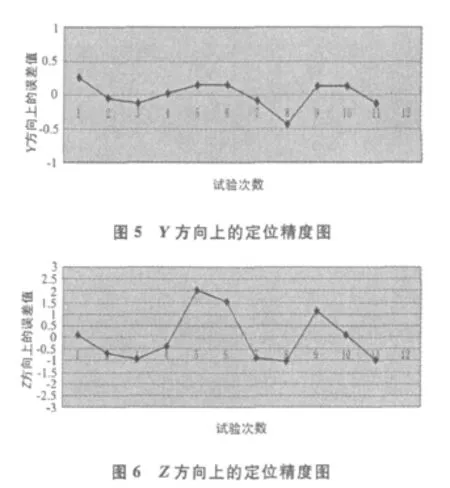
图4,5,6分别显示了该方法在测时精度为10-6s时,X、Y、Z方向的定位误差。由图可知,在X、Y方向上定位精度满足1 m的精度范围,在Z方向上精度基本满足米级精度。此方法的误差主要来源于信号接收器的接收时间误差。当接收条件较好,当测时精度满足10-9s时,其定位精度可以达到厘米级。

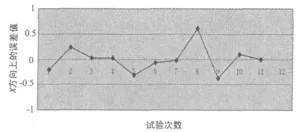
图4 X方向上的定位精度图

5 结 论

当信号接收器位于一个垂直面内时,通过测得目标到信号接收器的时间差,利用距离交汇模型可以求得目标在独立坐标系中的位置。由于该方法不要求水下目标带有精密时钟,节约了定位成本,且定位精度相对较高。此外,该方法可以对水下不同频率的目标进行定位。经测试该方法的最大作用距离可达到1 km,可以对5个目标进行定位。对于近距离多目标的识别和定位,提出一个新的解算方法,具有一定的实用价值。

[1]丁士圻等.船载式远程高精度水声定位系统[J].海洋工程,1996,14(4):16-21.

[2]蔡艳辉.差分GPS水下定位系统集成关键技术研究[D].辽宁工程技术大学,2005.

[3]任纪庆等.基于线阵水下定位的解析求解算法[J].全球定位系统,2009,34(5):20-22.

[4]李精文等.GPS水下定位的水声定位算法[J].华东船舶工业学院学报.1998,12(5):37-42.

[5]武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉大学出版社,2003.

[6]张 恒.多目标水声信号识别与检测水库实验报告[R].2009.