基于平均度与平均聚类系数的RWP模型的研究
2010-07-17蔡青松张迎新
周 密, 蔡青松, 张迎新
(北京工商大学 计算机与信息工程学院, 北京 100048)
随机路点(random way point,RWP)[1]模型由于其实现简单,便于用数学语言描述,被广泛应用在移动自组织网络(mobile ad-hoc network,MANET)研究中. 机会网络作为MANET研究的一个分支,其特点在于机会网络在大部分时间是非连通的,而传统的MANET主要考虑网络连通的情况. 在这种特殊性下,我们需要重新评估RWP模型是否适合作为描述机会网络的节点移动模型. 本文在前人的研究基础上继续对RWP模型进行深入的分析,并从复杂网络理论中引入平均度以及平均聚类系数两个重要的概念,通过与实验数据的比较,分析了RWP模型对机会网络节点移动模型的仿真效果.
1 平均度与平均聚类系数
1.1 平均度
某个节点i的度Di定义为与节点i所连的节点个数. 节点的度又有两个延伸概念,最小度与平均度. 一个网络中度最少的节点的度为网络的最小度,如果一个网络中最小度大于等于1则这个网络是连通的. 在文献[2]中讨论了有关RWP模型最小度的结论,但在机会网络节点构成的无向图中可能同时存在多个孤点. 一个n节点无向图可能是由一个n-1个节点的完全图和一个孤点构成,也可能是由n个孤点构成,如图1的(a)和(b). 这两种情况的最小度都是0,最小度不能适当的描述网络的连接性.
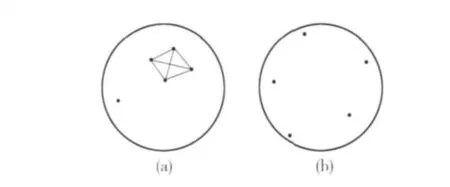
图1 两个最小度为0的无向图Fig.1 Two undirected graph with minimum degree zero
平均度为所有节点的度的算术平均值:
可以算出图1(a)的平均度为:
图1(b)的平均度为:
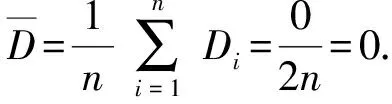
所以在机会网络中,使用平均度来表现网络的连接特性更为科学.
1.2 平均聚类系数
聚类系数是描述网络节点聚集程度的参数,节点i的聚类系数定义为:节点i的邻居之间所实际具有的边数与可能有的边数的比值. 即,
其中ki为节点i的度,即节点i的邻居数.Ei为这些邻居之间实际具有的边数.
由于单个节点的聚类系数受到该节点的移动路径的影响很大,所以可以通过计算全部节点的聚类系数并求其均值来观察整个网络的节点聚集情况. 网络的平均聚类系数定义为:
可以通过分析平均聚类系数随时间的变化来观察节点的聚集趋势.
2 RWP模型与实验数据
2.1 RWP模型的定义
RWP模型是一种理想化的分析模型,所以在RWP模型中有很多的假设条件,使得RWP模型在仿真移动自组织网络时有一定的偏差,很多文献中也都指出了RWP模型的节点分布并不均匀[3-4],但在真实环境下节点的分布往往也不是均匀的,如果RWP模型与真实环境下的这种非均匀性有某种关联或者相似性,那么使用RWP模型来作为机会网络的仿真节点移动模型就是合理的,或者说有相当的参考价值. 反之则需要用考虑使用其它的移动模型来仿真机会网络的节点移动.
下面给出RWP模型的定义:
初始分布函数为finit(x)的n个节点分布在模拟区域Q中,每个节点的运动相互独立,其中静止的节点数量占总结点数量的比例用ps表示,并假设节点在目的地的停留时间tp的概率密度函数为fTp(tp),移动节点的速度范围为[Vmin,Vmax]. 每个节点的随机移动过程可以用以i为标号的移动周期构成的集合{Di,Tp,i,Vi}i∈N来表示,每个移动周期中,节点先停留Tp,i,再以速度Vi向Di匀速移动. 其中Di是模拟区域内随机选定的目的位置;Tp,i为该移动周期中停留的时间,其概率密度函数为fTp(tp);Vi表示在这个移动周期中节点的移动速度,在[Vmin,Vmax]中选取.
2.2 RWP模型仿真数据的生成
我们在实验中使用卡内基梅隆大学开发的RWP模型仿真工具setdest[5-6]生成仿真数据. 为了得到比较典型的数据,使用长方形的模拟区域,设定全部节点都是移动节点,停留时间设为常量并规定节点的初始分布为二维均匀分布.
为了形象的说明,下面以一条命令为例说明:
./setdest-v 1 -n 10 -p 20 -M 15 -t
2000 -x 500 -y 800
该命令代表如下的RWP模型场景:在一个500 m×800 m的区域里面均匀分布着10个节点,每个节点在移动周期开始时先停留20 s,然后在仿真区域里随机选择一个目的位置,然后在(0,15]之间随机选定一个速度(单位:m/s),匀速向目的点移动. 到达目的地以后再开始下一个移动周期,整个运动过程持续2 000 s.
2.3 实验数据
研究所用的真实实验数据来源于2006年西班牙巴塞罗纳INFOCOM06期间,剑桥大学进行的实验六[7](Exp6). 项目组分发给与会的学生和研究员便携的小型设备来采集连接信息,实验计时从2006年4月23日凌晨开始,到23日下午5点钟所有设备全部启动,持续到4月27日. 在整理好的实验数据中节点标号1~20的为固定节点,21~98为携带在与会的学生和研究员身上的便携设备.
需要说明的是,由于实验中使用的只是测试连接性的便携设备,每个设备的开启时间和扫描周期会有个体差异,在实验数据中往往会有下面2种情况:
1)节点相遇持续时间为零
在实验数据中节点A与节点B建立连接时间和连接失效时间相同,这意味着在连续两次扫描时间内,两个节点就离开了彼此的通信范围,很明显这种情况在实际中无法完成数据的交换,在本文对应的实验中将其处理为无效的连接数据,不参与计算参数的计算.
2)连接的不对称性
在实验数据中同一时刻,节点A有扫描到节点B的记录,但B没有相应的扫描到A的记录,考虑到扫描的时间不是完全同步的,而且计算连接性的时间抽样点也是离散的,研究假设在这种情况下A和B是可以进行通信的. 在计算某时刻平均度和聚类系数时只要两个节点其中之一可以连接到另外一个节点就按双向连接计算.
3 关键参数的对比分析
3.1 节点的平均相遇持续时间
相遇持续时间是指两个节点进入彼此的通信范围到离开对方的通信范围之间的时间,通过两组实验来观察RWP模型中节点平均相遇持续时间的规律.
第一组实验,在长宽都为500 m的模拟区域内进行100 000 s的模拟,节点最大移动速度为50 m/s,停留时间从0 s变化到1 000 s,结果如图2.
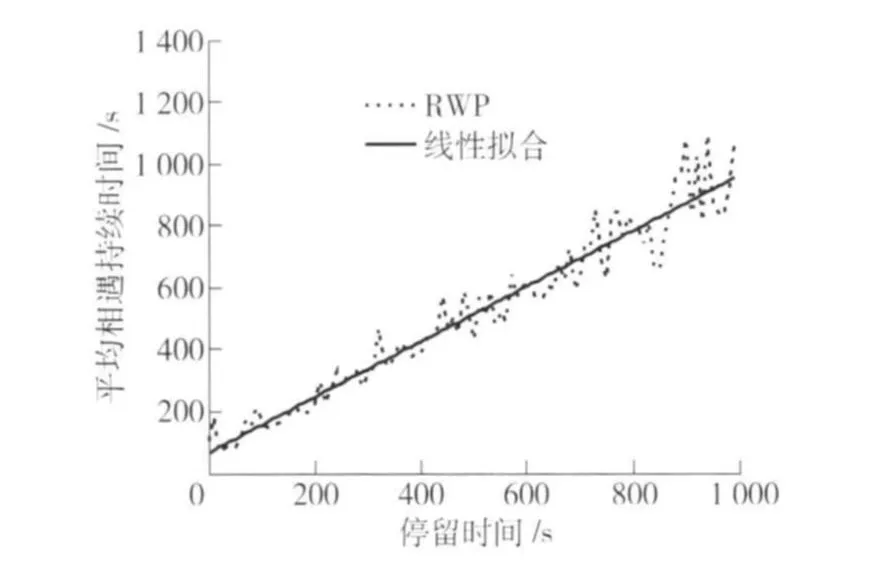
图2 平均相遇持续时间与停留时间的关系Fig.2 Average contact duration and pause time
平均相遇持续时间与拟合直线符合度很高,说明相遇持续时间与停留时间成线性关系.
从RWP模型的定义可以知道节点的一个运动周期分为两个阶段,一个是停留阶段,一个是移动阶段. 当最大速度一定时,停留时间越长则停留阶段在运动周期中所占的时间比例也就越高,节点的整体移动性下降,因此导致平均相遇持续时间也呈线性增长,实验的结果与理论是相符的.
第二组实验,固定停留时间为50 s,再让节点最大移动速度从1 m/s变化到100 m/s,可以看到停留持续时间急速下滑后趋于稳定,在对数坐标系下呈一条直线,可以被幂率分布曲线很好的拟合,如图3.

图3 平均相遇持续时间与最大运动速度的关系Fig.3 Average contact duration and max speed
图3给出的直观含义是当节点移动性较弱,停留阶段占移动周期的比例很高时,节点移动速度对网络的拓扑的稳定性影响很大;而当停留阶段占移动周期的比例变小以后,节点的移动速度对网络拓扑的影响力也急剧变小.
而实际上这种现象证明了RWP模型节点的聚集效应的存在[8],由于RWP模型中节点在每个移动周期选择目的点的方式是在仿真区域内随机选取,所以必然导致节点有像仿真区域中间移动的趋势. 对于机会网络来说,比如人类的社会活动当中,人们也会有向某个中心聚集的趋势:上课时学生会向教室聚集,超市购物时消费者会向收银台聚集等,所以存在使用RWP模型仿真机会网络具有合理性的可能.
3.2 节点的相遇时间间隔
相遇时间间隔表示两个节点在两次相遇之间经历的时间,在文献[9]中,通过实验数据得到了在机会网络中节点相遇时间间隔为幂率分布的结论.
通过实验来观察RWP模型中相遇时间间隔的分布情况,如图4.
可以在图4中看出在对数坐标系下,相遇时间间隔的分布呈一条直线,这说明了RWP模型的相遇间隔时间与机会网络相似,也服从幂率分布.
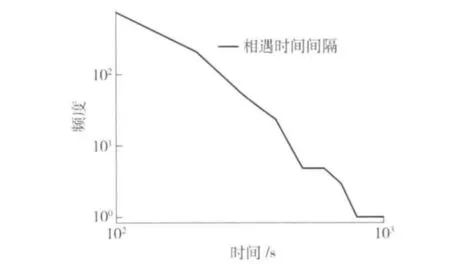
图4 RWP模型中相遇时间间隔的分布Fig.4 Distribution of inter-meeting time in RWP model
3.3 网络平均度和平均聚类系数
虽然在前面的分析中,看到RWP模型与机会网络单个节点随时间变化的参数十分相似,但所有节点构成的网络拓扑的规律仍有待考察,下面使用平均度和平均聚类系数来分析仿真数据和实验数据的聚集特性.
setdest仿真条件为:1 000 m×1 000 m的区域里均匀分布的50个节点,停留时间为0 s,最大速度为10 m/s,仿真时间为1 000 s. 与之对比的实际数据为Exp6. 将仿真数据和实验数据整理成同样的数据格式来观察平均度和聚类系数的关系.
观察图5(a)和图5(c)可以很清晰地发现在仿真开始时RWP模型的变化幅度很大,这是由于研究简单地假定RWP模型的初始分布为均匀分布,而实际上在xm×ym的矩形模拟区域中,RWP模型稳定的分布函数可以近似为:
这种现象称为RWP模型的初始效应,为了和实验数据做对比,观察RWP模型在实验时间到达250 s基本稳定以后的数据. 对于用来对比的Exp6的数据,研究认为60 000 s以后的实验数据为有效值,因为60 000 s以前的波动是由于那个时段在夜里,作为节点的实验人员的活动与RWP的仿真参数不符合.
通过对比图5(a)、(b)、(c)和(d)可以看出,RWP仿真数据的平均度和实验数据平均度的浮动区间大概在4到6之间;RWP模型的聚类系数的变化区间为0.57到0.72,而此时图5(d)实验数据中聚类系数的变化范围在0.11到0.28之间.
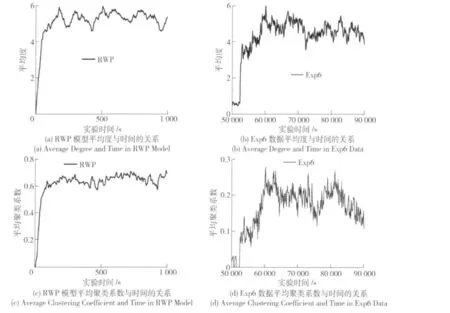
图5 RWP模型与Exp6数据的参数对比Fig.5 Comparison between RWP model and Exp6 Data
平均度是体现机会网络连接特性的参数,当两个机会网络的平均度相近时,说明两个网络的连接性也应该是接近的,RWP模型与Exp6数据在平均度相近的情况下,RWP模型的平均聚类系数却远远高于Exp6,说明RWP模型的连通性要比机会网络理想得多,而机会网络中会存在更多更小的子网和孤点,正是由于小子网和孤点的大量存在导致了机会网络的聚类系数要低于RWP模型的仿真结果. 如果使用RWP模型来仿真机会网络的节点移动,会对网络的连通性有过高的估计,在这样条件下满足要求的路由协议显然无法满足实际的需要.
4 结 论
本文对比分析了RWP模型和Exp6数据中反应移动模型特性的参数,分析数据表明RWP模型中节点间相遇持续时间与相遇时间间隔的分布情况与机会网络类似,但从整个网络的节点聚集情况来看RWP模型的仿真结果过于理想化,因此不适合作为描述机会网络的仿真移动模型.
尽管RWP模型的聚类特性与机会网络不同,但是作为经典的移动模型RWP在MANET研究中的重要意义是不能否认的. 机会网络中节点移动的规律十分复杂,很难用数学语言来描述,但可以以对RWP模型的研究为基础,找到更适合描述机会网络的移动模型.
本文得到的结论对于机会网络和MANET的研究都有一定的参考价值,找到适合描述机会网络的移动模型还需要进行其它的对比实验,真正实现可以投入应用的MANET还需要通过长期的探索和研究.
