等效阻力法在感潮河段桥墩群概化中的运用研究

唐 磊 ，张 玮 ，解鸣晓 ，张庭荣 ，余 珍

（1.河海大学港口海岸与近海工程学院，南京210098；2.河海大学水资源高效利用与工程安全国家工程研究中心，南京210098；3.交通部天津水运工程科学研究所工程泥沙交通行业重点实验室，天津300456；4.广东省水利水电科学研究院，广州510610）

在跨江跨海大桥、海上风电场以及淤泥质海岸港口码头等工程中，往往采用桩墩基础来承载上部建筑物的荷载，大量桩墩打入水中，对其周围的水位、流速等势必造成影响。以往主要采用物理模型和数值模拟手段开展桩墩对水流条件影响的研究。随着计算机技术的不断发展及数值计算方法的不断完善，桩墩数值模拟越来越受到广大科研工作者的关注。在数值计算中，为了保证工程方案的实施不影响模型的开边界，或为了适应工程海区水流特点，数学模型往往取较大的范围，可达数十至数百公里［1］，而桩墩尺寸较小，在数十厘米至数十米之间，构成了桩墩模拟计算中的“大水域、小尺度”这样一对矛盾，是工程研究中的难点。

目前大范围模型中的小尺度桩墩数值模拟方法有2种，即间接模拟法和直接模拟法。间接模拟法将桩墩作为过水区域处理，对桩墩所在网格的糙率或高程进行修正，可总结为局部糙率修正法和局部地形修正法［2-3］，该模式不必描述桩墩外形，可以加大计算网格尺度、减少计算耗时。直接模拟法是将桩墩作为不透水的岸边界来处理，通过对桩墩边界的网格加密，细致刻画出桩墩的外轮廓线，所得流场较为真实可靠，当然随着网格数量的增加，特别是网格尺度的急剧减少，所得模型耗时较多。为了缩短计算时间，文献［4］在直接模拟法中提出了概化方法，如等阻水面积概化法。文献［5］在分析以上几种方法优缺点的基础上，从直接模拟法的角度，提出了一种新的桩墩概化方法——等效阻力法，并从水位、流速、壅水等几个方面，论述了该方法的优点。该方法是从数值水槽试验中提出的，且研究的水流条件仅限于恒定流范畴，而在非恒定条件下能否适用，特别是在感潮河段，概化所需的水动力条件如何选取，均值得深入研究。

针对上述问题，本文以长江下游苏通大桥桥墩为例，分析运用等效阻力法概化桥墩群后，对大范围水位及流速的影响；同时对比分析长江下游徐六泾河段各岔道在概化前后的分流比变化情况，探讨等效阻力法在感潮河段桥墩群概化中的适用性。

1 模型建立

1.1 控制方程及求解

水流连续方程

水流运动方程

式中：x、y为水平坐标轴；t为时间，s；η 为水面高程，m；h 为总水深，m；u、v分别为 x、y方向的垂线平均速度，m/s；f为柯氏参数；ρ为水流密度，kg/m3；g 为重力加速度，m/s2；A 为水平涡粘系数，m2/s；τsx、τsy、τbx、τby分别为x、y方向的表面和底部应力，N/m2。

为了较好地贴合蜿蜒河道岸线，采用三角形无结构网格剖分技术进行网格剖分；利用有限体积法（Finite Volume Method）进行数值求解，并采用陆地动边界技术，模拟感潮河段的露滩现象。求解技术及模式验证过程详见文献［6-7］。

1.2 模型及苏通大桥概况

模型范围上起南通天生港（32°01′N，120°45′E），下至北支青龙港（31°51′N，121°14′E）及南支杨林潮位站（31°35′N，121°15′E），模型包括通州沙、狼山沙、新通海沙、白茆沙等沙洲，沿程长约 77.5 km，水域面积约668.5 km2。研究对象为长江下游感潮河段跨江大桥——苏通大桥桥墩群，共有72根大小不一的桥墩，最小尺寸为6 m×15 m（长×宽，下同），最大尺寸为48.1 m×113.7 m（图1，高程为国家85黄海基准面）。

图1 模型范围Fig.1 Domain of model

1.3 参数率定及验证

选取大潮作为代表潮型，时间从2007年10月27日10时至2007年10月28日13时，由于模型位于长江口感潮河段范围内，同时受潮流与径流的影响，为了使计算域内潮流场能够反映实际的潮流运动，模型开边界条件均由各潮位站实测资料提供；模型计算时间步长Δt=30 s，糙率根据水深条件设置，给出随水深变化的糙率场，取0.012 5～0.02。

潮流验证参见文献［8］。潮位过程计算值在相位、数值上与实测值吻合较好，误差一般小于0.1 m；潮流流速及流向过程计算值在相位、数值上也与实测值吻合较好，满足规范要求。表明所建立的数学模型合理可信。

2 桩墩群概化思路研究

2.1 桩墩群概化思路

在水流模型中，一般网格尺度即可满足水动力模拟精度要求（数值、相位等）。然而，当考虑桥墩等小尺度阻水建筑物对水流影响时，势必要通过加密网格的方法来反映建筑物的外轮廓，而随着网格数量的增加特别是网格尺度的急剧减小，必将消耗大量的计算时间。为减少计算耗时，在确保大范围水动力条件不变的前提下，有必要对桩墩进行适当的概化。

在保证概化前、后阻力相等的前提下，概化方案可以有多种，但从实际工程角度出发，概化过程中必需注意：（1）主、辅通航孔桥墩尺寸、平面位置保持不变。桥梁工程中，为了保证航运及断面过流能力的要求，往往设有主通航孔、辅通航孔及一般性过流孔，而主、辅通航孔处的桥墩尺寸往往较大，且其位置具有标志性作用，概化过程中不可改变其尺寸及平面位置；（2）概化前后，桥墩群轴线位置保持不变。运用等效阻力法概化桥墩，其本质就是放大原桩尺寸、减少桩墩个数，并在水平位置向上重新排列布置，用阻力最佳逼近方法获得概化形式，概化桩的水平位置存在多种选择，而保持桩墩群轴线原始面貌的应当为优选方案；（3）概化前后，涨、落潮水流平均阻力应分别相等。在感潮河段，潮涨潮落使水流具有往复流特性，因此应对涨、落潮阻力分别进行校核，所得方案涨、落潮平均阻力应尽量保证与原状桩墩相等。

2.2 桩墩群概化步骤

跨江大桥桥墩往往有几十至百根之多，很难获得拟建桥墩处的流速、流向等水文资料，而水动力数学模型作为一种拓展资料的有效手段，可为研究提供相应的水流条件。因此有必要建立一定范围的数学模型（无桥墩），经计算并充分验证后，为桩墩群概化提供水动力资料。水流阻力计算公式如下

式中：Fw为水流力标准值，kN；V为水流流速，m/s；Cw为水流阻力系数；ρ为水的密度，t/m3，淡水取1.0，海水取1.025；A为计算构件在与流向垂直平面上的投影面积，m2。

使用等效阻力方法的概化步骤如下：

（1）采用文献［10］中提出的水流阻力系数Cw计算公式，相关参数参照《港口工程荷载规范》选取，计算原单桩墩逐时水流阻力（水动力条件由无桥墩的数学模型提供），并统计原单桩墩的涨、落潮时段及全潮平均阻力，分别记为 fDFi、fDEi、fDAi；

（2）对拟概化桥墩群进行区域划分。如对苏通大桥桥墩群概化，以辅通航孔桥墩（即主 3、主 6）为界（图 1），对南北两侧桥墩群分别进行概化；

（3）以北侧桥墩群为例，统计北侧原桥墩群的涨、落潮时段及全潮总平均阻力，分别记为 FDF、FDE、FDA；

（4）预估一个概化单桩尺寸（以方桩为例），选取北侧原桥群轴线中央处的水动力条件（无桥墩模型提供），计算概化单桩的涨、落潮时段及全潮平均阻力，分别记为 f′DF、f′DE、f′DA，并用 FDF、FDE、FDA分别除以 f′DF、f′DE、f′DA，并反复调整预估桩尺寸，得到概化桩的数量n；

（5）在北侧原桥墩群轴线上，对概化桩进行等距布置，获得各概化桩的水平坐标；

（6）从无桥墩的数学模型中提取概化桩处的水动力条件，按步骤（1）、（3）计算北侧概化桩墩群涨、落潮时段及全潮总平均阻力 F′DF、F′DE、F′DA；

（7）对比分析北侧概化桥墩群与原桥墩群的涨、落潮时段及全潮总平均阻力，如不满足阻力相等条件，则应重新估计概化桩尺寸，返回至步骤（4）重新计算，直至满足阻力相等为止。

南侧桥墩群概化方法与北侧相同。具体结果见表1，由表1可以看出，概化桩尺寸较原桩大幅增加，且根数约为原桩的30%。

表1 原桩与概化桩的参数Tab.1 Parameters of the original piers and simplified piers

2.3 概化阻力分析

选取总平均阻力来判别桩墩概化前后阻力的等效性，总平均阻力定义为断面上所有单桩的平均阻力之和。表2中列出了桥墩群概化前后涨、落潮时段及全潮总平均阻力等信息。结果表明，在同一种概化方案中，全潮总平均阻力误差为3%左右，落潮总平均阻力误差较小，而涨潮误差稍大，为6.3%；从阻力近似相等角度来讲，选择的概化桩尺寸是基本合理的。

为了进一步说明采用总平均阻力作为判别要素的合理性，分析了涨、落急及高潮位时刻的总阻力误差，结果表明，涨、落急时刻总阻力误差分别与涨、落潮总平均阻力一致、高潮位时刻总阻力误差与全潮总平均阻力一致，说明本文采用的概化方案是一个综合结果，满足高潮位时刻阻力相等的同时，还兼顾了涨、落急时刻的阻力相等条件。网格示意图见图2，对应的网格最小尺度为6 m、6 m、11.1 m。

表2 阻力及误差Tab.2 Resistance and error

图2 桥桩周围网格布置图Fig.2 Plane layout of grids around the bridge piers

3 桥墩群概化效果分析

为了分析等效阻力法概化桥墩后的效果，本文从水动力（水位、流速及断面分流比）、时间效益等多个角度对其进行检验。由式（4）可知，在一定的Cw条件下，阻力与V2和A的乘积成正比；恒定流中，水流阻力仅与流速有关，就感潮河段的非恒定流而言，在潮流作用下，流速及迎水面积均随水位的升降而不断变化，进而水流阻力也随时间变化。图3中给出了苏通大桥主5桥墩附近的潮位、流速及水流阻力过程线，反映出最大水流阻力并非出现在高潮位时刻，而出现在最大流速时刻，这时桩墩对水流的影响亦最大。因此，本文将采用涨、落急时刻的水动力条件来检验等效阻力法的概化效果。

3.1 水位变化分析

在苏通大桥北侧桥墩群、主4墩、主通航孔及南侧桥墩群处，设置长约3 km的观测断面（A、B、C、D），每个断面上布设100个观测点，为了细致地刻画出桩墩附近水面线情况，在桩墩附近约1.8 km范围内每20 m布置一个点，其余均为100 m取一点（图1）。分别绘制了各观测断面在涨（落）急时刻的水面线（图4～图5），图4与图5中误差曲线为概化桥墩与原状桥墩模型的差值。

图3 潮位、流速及水流阻力过程线（2007-10-27）Fig.3 Hydrograph of tidal level，velocity and resistance

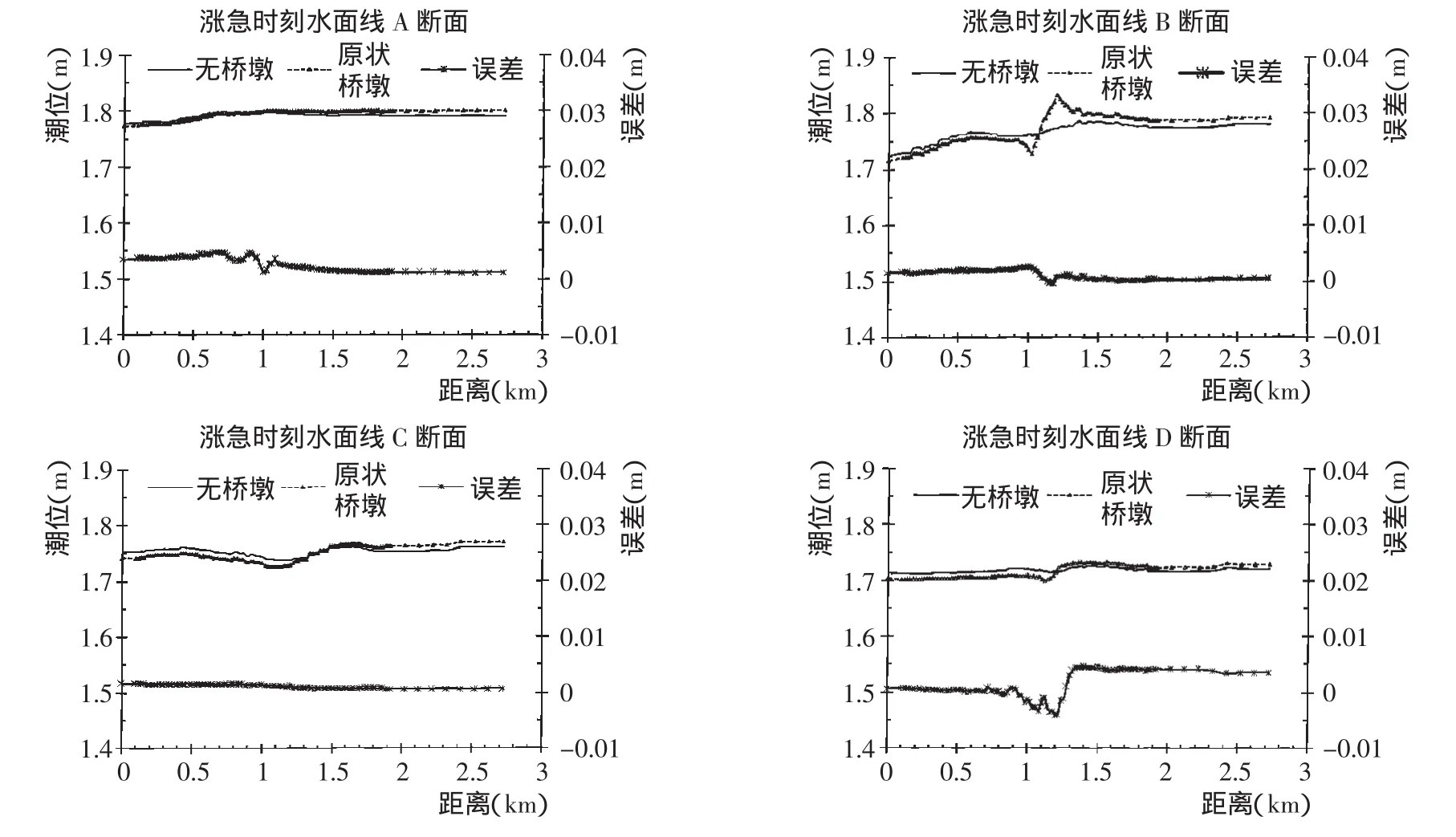
图4 涨急时刻水面线Fig.4 Water-surface profile at maximum flood

图5 落急时刻水面线Fig.5 Water-surface profile at maximum ebb

图4～图5表明：（1）桥墩对水位影响距离较远，但数值上较小，为厘米量级；（2）原状、概化桥墩模型均可模拟出涨、落急时刻桥墩上游壅水和下游跌水的现象，此处上、下游概念与来流方向有关；（3）误差曲线表明，运用等效阻力法概化的桥墩模型与原状桥墩模型计算所得涨、落急时刻的水面线结果在数值上吻合较好，误差控制在毫米量级；然而在桩墩附近和观测断面D上误差稍大，前者由于概化桩的尺寸及平面位置较原桩均发生变化；后者是由于在概化中南侧桩群的全潮总平均阻力人为增加了近3%。

总的来讲，采用等效阻力法概化桥墩模型的水位计算结果与原桩模型吻合较好，可认为该方法有效，不会造成大范围内水位场的失真。

3.2 流速变化分析

分析桥墩群概化前后涨、落急时刻流速的变化情况，包括流速变化率和影响距离分析，探讨等效阻力法概化桥墩群对区域内流速的影响。概化前后的流速变化率定义为

式中：α为概化前后流速变化率，%；VA为概化后最大流速，m/s；VP为概化前最大流速，m/s。

按式（5）计算概化前后最大流速变化率，并绘制涨、落急时刻流速变化率等值线（图6），不同流速变化率包络线与桩墩轴线间的距离（定义为桩轴线至流速变化率等值线处的距离）统计结果见表3。结果表明：（1）不论涨潮还是落潮，流速变化率超过5%的等值线均集中在桩墩周围很小的范围内；影响距离相对较小，涨潮时期，北侧最大影响距离为概化桩径的16倍，南侧为13倍；落潮时期，北侧最大影响距离为概化桩径的18倍，南侧为17倍；（2）不论涨潮还是落潮，主通航孔内最大流速变化率几乎为0；（3）不论涨潮还是落潮，桩墩附近2%流速变化率包络线范围有所增加，涨潮时期，北侧最大影响距离为概化桩径的23倍，南侧则为24倍；落潮时期，北侧最大影响距离为概化桩径的43倍，南侧则为31倍。

上述结果表明，概化桩墩群对大范围的流速影响甚微，仅在桩墩群周围很小范围内，流速存在小幅度的失真，这与概化桩对水位的影响是一致的。因此认为采用等效阻力法概化桥墩不会对大范围内的流速场造成失真。

图6 概化前后涨（落）急时刻流速变化率Fig.6 Changing rate of velocity between the simplified and original bridge piers at maximum flood/ebb

表3 不同流速变化率包络线与桩墩轴线间的距离Tab.3 Distance between the different envelopes of velocity changing rate and the center line of piers m

3.3 分流比变化分析

在狼山沙、南北支及南支白茆沙水道分别设置测流断面，计算各断面在无桥墩、原桥墩及概化桥墩情况下的逐时流量。在统计分流比时，考虑到该河段落潮流对河床塑造起主导作用，因此采用落潮稳定时期的分流比作为分析对象，相关统计结果见表4。结果表明：（1）对比分析无桥桩与原桥桩模型，发现桥墩群对徐六泾河段各汊道分流比均有一定程度的影响，其中狼山沙西水道受影响程度稍大，约为1.5%，其余水道稍小，均小于0.5%，说明建立该河道范围内的数学模型时，需要考虑苏通大桥桥墩群的影响；（2）对比分析原桥桩与概化桥桩模型，发现各汊道的分流比在上述2种模型下分别对应相等，说明采用等效阻力法概化的桩群对各汊道分流比的影响与原状桥墩群完全一致，该方法不会造成分流比的失真。

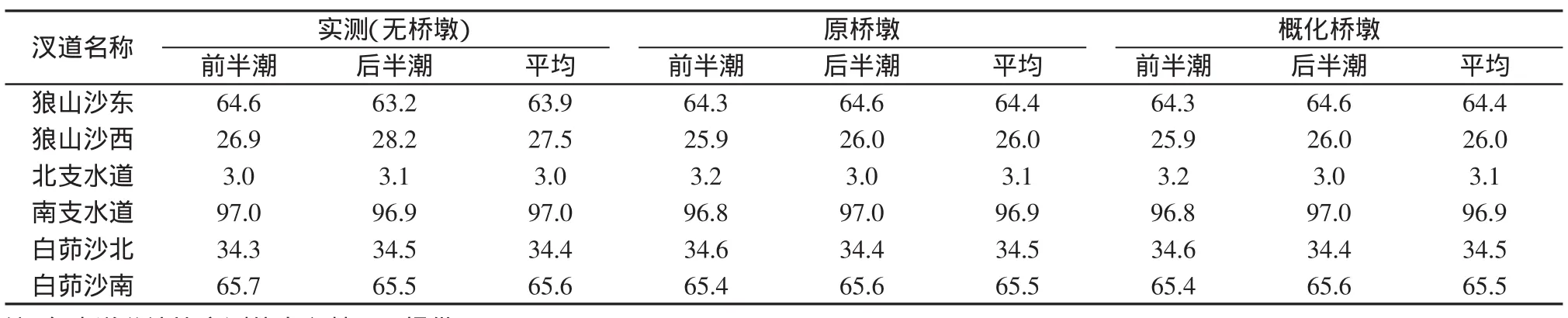
表4 各汊道分流比Tab.4 Diversion ratio of each river branch %

对水位、流速及断面分流比变化的分析认为，运用等效阻力法概化桩群不会对大范围内的水动力造成影响，微小失真只存在于桩周附近，且该处的水动力情况不是本文的重点。因此将等效阻力法运用于苏通大桥桥墩群概化是完全可行的。

3.4 计算时间效益比较

概化模型往往用一定的计算精度换取可观的计算时间效益，此次用于计算的PC机的CPU主频为1.86 GHz，内存为3 G。网格参数及计算耗时见表5。本文采用有限体积法对模型进行数值求解，因此其计算时间主要受控于最小网格尺寸及计算机整体性能。从表5可以看出，与原状桩墩群模型相比，运用等效阻力法概化桩墩群模型约减少了一半的计算时间。

表5 网格参数及计算耗时Tab.5 Parameters of grids and calculation time

4 结论

采用有限体积法为基础的二维潮流数学模型，以长江下游感潮河段苏通大桥桥墩群为例，采用等效阻力概化方法，给出了概化桩群的具体步骤，提出了采用总平均阻力作为判别阻力等效性的标准，从水动力（水位、流速及断面分流比）、时间效益等多个角度探讨了等效阻力概化法在该河段的适用性，研究结果表明，该方法运用于苏通大桥桥墩群概化是完全可行的，对类似工程亦具有借鉴意义。具体结论如下：（1）采用总平均阻力作为判别桩墩概化前、后阻力等效性的标准，涨、落及全潮总平均阻力误差分别为5.4%、0.9%、3.3%，而涨、落急及高潮位时刻总阻力误差分别为5.5%、-0.3%、3.5%，说明本文采用的概化方案是一个综合结果，满足高潮位时刻阻力相等的同时，兼顾了涨、落急时刻的阻力相等条件。（2）除桩墩周围存在微小失真外，原状与概化桥墩模型计算所得涨、落急时刻的水面线结果在数值上吻合较好，说明采用等效阻力法概化桥墩不会造成大范围内水位场的失真。（3）不论涨潮还是落潮，流速变化率超过5%的等值线均集中在桩墩周围很小的范围内；影响距离相对较小，涨潮时期，北侧最大影响距离为概化桩径的16倍，南侧为13倍；而落潮时期，北侧最大影响距离为概化桩径的18倍，南侧为17倍。不论涨潮还是落潮，桩墩附近2%流速变化率包络线范围较大，影响距离相应较大，涨潮时期，北侧最大影响距离为概化桩径的23倍，南侧则为24倍；落潮时期，北侧最大影响距离为概化桩径的43倍，南侧则为31倍。说明采用等效阻力法概化桥墩不会造成大范围内流速场的失真。（4）对比分析无桥桩与原桥桩模型，发现桥墩群对徐六泾河段各汊道分流比均有一定程度的影响，其中狼山沙西水道受影响程度较大，约为1.5%，其余水道较小，均小于0.5%，表明在建立该河道范围内的数学模型时，需要考虑苏通大桥桥墩群的影响；对比分析原桥桩与概化桥桩模型，发现各汊道的分流比在上述2种模型下分别对应相等，这说明采用等效阻力法概化的桩群对各汊道分流比的影响与原状桥墩群完全一致，不会造成分流比的失真。（5）苏通大桥桩群概化后，其计算耗时较原状桩墩群模型大约缩减一半。

本文的概化桩布置采用等距分配的方法，而实际工程中地形复杂，是否存在更为有效的布置方式、更为准确的概化原则，是值得深入研究的；同时本文研究对象可视为单排桩，而对于沿岸建设多排桩的建筑物如高桩码头和栈桥等情况，该方法是否适用还亟待进一步研究。

［1］李孟国.局部模型在工程潮流数值模拟中的应用［J］.水道港口，2001，22（2）：61-65.LI M G.Application of Local Models in Tidal Flow Numerical Simulations［J］.Journal of Waterway and Harbor，2001，22（2）：61-65.

［2］唐士芳.桩和桩群的水流阻力及其在潮流数值模拟中的应用［D］.大连：大连理工大学，2002.

［3］曹民雄，甘小荣，周丰年，等.潮汐河段桥墩对水流影响的数值计算与分析［J］.人民长江，2006，37（4）：81-84.CAO M X，GAN X R，ZHOU F N，et al.Numerical modeling of the flow field under the impact of bridge piers in tidal river［J］.Yangtze River，2006，37（4）：81-84.

［4］张玮，王斌，夏海峰.近海风电场风机桩群布局对海域水动力条件的影响［J］.中国港湾建设，2007（2）：1-4.ZHANG W，WANG B，XIA H F.Impact of Layout of Pile Groups as Foundation for Offshore Wind Power Generators upon Hydrodynamic Conditions［J］.China Harbour Engineering，2007（2）：1-4.

［5］解鸣晓，张玮，谢慧姣.桩群数值模拟中的概化方法研究［J］.水动力学研究与进展，2008，23（4）：464-471.XIEMX，ZHANGW，XIEHJ.Simplificationmethodinnumericalmodelingofbridgepiergroup［J］.ChineseJournalofHydrodynamics，2008，23（4）：464-471.

［6］胡四一，谭维炎.无结构网格上二维浅水流动的数值模拟［J］.水科学进展，1995，6（1）：1-9.HU S Y，TAN W Y.Numerical Modeling of Two-Dimensional Shallow Water Flows on Unstructured Grids［J］.Advances Water Science，1995，6（1）：1-9.

［7］谭维炎.计算浅水动力学——有限体积法的应用［M］.北京：清华大学出版社，1998.

［8］张玮，胡凤彬，唐磊，等.南通通海港区新江海河口内港池水流条件及泥沙回淤研究［R］.南京：河海大学，2008.

［9］JTJ215-98，港口工程荷载规范［S］.

［10］邓绍云.桩柱水流绕流阻力特性及其计算［J］.中国港湾建设，2007（1）：4-6.DENG S Y.Drag Force Characteristics and Calculation of Water Flow around Pile［J］.China Harbour Engineering，2007（1）：4-6.

［11］杜亚南，施慧燕，高健，等.国电海门电厂水文测验技术报告［R］.上海：长江委水文局长江口水文水资源勘测局，2007.