基于粗糙集理论的汽轮机组振动故障诊断决策网络模型

王海亭,张珂,梅林,王秀江

(大唐七台河发电有限责任公司,黑龙江省七台河市154600)

汽轮机组振动的复杂性和耦合性使汽轮机的振动故障具有多层次性和随机性特点,因此很难在故障原因与故障征兆之间建立对应关系。为了全面地刻画汽轮发电机组振动故障模式,提高故障诊断的精度,一般要求提取大量的故障征兆,但这些征兆在故障诊断过程中的重要性并不相同,甚至某些征兆是冗余的[1],不仅造成诊断资源的浪费(需要获取代价、处理时间和存储空间),而且直接影响到生成简洁高效的诊断决策规则,影响了故障诊断的效率和实时性[2]。

本文将针对故障诊断问题的冗余性和不一致性,把汽轮机故障数据进行离散化处理,建立故障诊断决策表,形成知识库,然后采用粗糙集数据挖掘方法,从决策表中推理出故障诊断网络模型以及提取诊断规则,为故障诊断提供可靠依据[3]。

1 粗糙集理论

Rough Set理论是Z.Pawlak于1982年提出的一种处理模糊和不确定知识的数学工具,它可以在保持分类能力不变的前提下,通过知识约简导出问题的决策或分类规则,为信息系统或决策系统提供潜在知识和决策支持[4]。

1.1 粗糙集理论的基本概念

对于知识表示系统可以用下式表达:

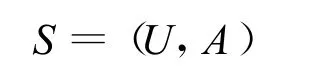
式中:S为粗糙集合;U为非空有限集合;A为属性集合。设B⊆A,X⊆U,定义 X的B下近似分别称为X在B下的正域、负域和边界。

令故障诊断决策系统为S={U,C,D},其中C为故障征兆属性集合,D为故障决策属性集合。令U/IND(C)表示根据故障征兆属性C将U上的对象进行划分而得到的所有等价类,等价类的数量用n表示。a(xj)是样本 xj在属性a上的取值。S的分辨矩阵(cij)n×n:

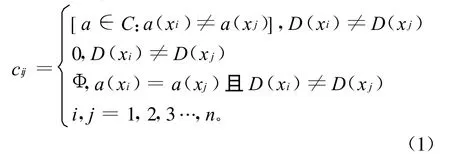
1.2 知识表示系统和决策系统

知识表示系统可以用下式表达:

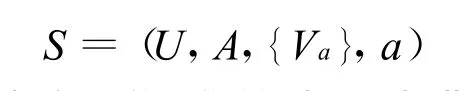
式中:U为非空有限集,称论域;A为非空有限集,称属性集合;Va为属性a∈A的值域;U→V a为单射,利用这个单射,论域U中的任一属性a可以在Va中得到某个唯一值。

如果A是由条件属性集合C和结论属性集合D组成的,并且C和D满足C∪D=A,C∩D=Φ,则称S为决策系统。当结论属性集合D只包含一个元素d时,也可以用(U,C∪{d})表示决策系统;对决策系统S=(U,C∪{d}),BC是条件属性集合C的一个子集,称二元关系ind(B,{d})={(x,y)∈U×U:d(x)=d(y)或者 a∈B,a(x)=a(y)}为 S的不可分辨关系,其中,x和y为U中的元素[5]。

2 机组振动故障诊断决策网络模型

机组振动故障诊断决策网络模型的获取方法是通过构造一个具有不同简化层次的故障诊断决策网络来实现的,在定义了诊断决策规则置信度和覆盖度的概念、计算出各个节点上满足预先给定的诊断决策规则提取原则,获得诊断决策规则集之后,便可以利用此模型对新的故障状态进行推理和决策。

2.1 决策规则的置信度和覆盖度

置信度只能作为依据该决策规则得到正确结论的概率估计,而不能表达该决策规则在决策系统的同类决策中的覆盖程度,即该决策规则是基于多少决策相同的实例而得到,这一信息在故障诊断的推理中是很重要的,因此引入一个评价诊断决策规则的新指标——决策规则的覆盖度[6]。

2.2 机组振动故障诊断决策网络模型的构造

据分辨矩阵,可得故障诊断决策系统的分辨函数,将分辨函数化为析取范式,则每个子式所包含的征兆属性构成一个约简。将获得的所有约简作为决策网络模型的初始节点,并且将包含征兆属性数目相同的节点放置在网络的同一层;然后依次从每个节点中去掉一个征兆属性,得到该节点的后继节点,依此类推,直到节点无征兆属性变为空节点为止[7]。

综合考虑诊断决策规则的置信度和覆盖度,并按照下述步骤对各节点的诊断决策规则进行筛选。

(1)由上到下、由左至右依次计算决策网络各节点所获取的诊断决策规则的置信度,只将置信度大于预先给定的诊断决策规则置信度阈值的规则存入该节点的规则集中,同时计算该规则的覆盖度。

(2)如果某节点的所有决策规则的置信度都小于阈值,则选择置信度最大的两条诊断决策规则存入该节点的规则集中。在置信度相同的情况下,覆盖度大的诊断决策规则优先入选,可以避免由于某些节点规则集为空导致规则匹配无法进行,使网络推理具有良好的适应能力和较强的匹配能力。

3 决策网络模型的推理及规则综合评价

3.1 模型的推理

应用所构造的汽轮机组振动故障诊断决策网络模型进行故障的推理和决策时,可根据己知描述机组振动故障诊断问题的信息在网络中逐层匹配,给出机组振动故障诊断问题的最优解。

(1)用新的振动故障状态具有的故障征兆属性集合,由上至下寻找网络中的节点。

(2)如果存在这样的匹配节点,取匹配的每一个节点,用匹配上的征兆属性的值匹配该节点的诊断决策规则集,若存在匹配规则,则返回相匹配的诊断规则,并停止推理;否则,进入步骤(3)。

(3)取该节点的所有后继节点,对其中的每一个节点,重复进行步骤(2),直到结束。

在上述过程中,层次高的节点的诊断决策规则集优先进行匹配;对于同一层的节点,置信度大的规则优先匹配,在置信度相等的情况下,覆盖度大的诊断决策规则优先匹配。因为这样可以充分利用待诊数据中所含有的信息,得出令人信服的诊断结论。

3.2 规则的综合评价

在将待处理的数据对象与决策网络进行匹配后,返回的诊断决策规则集可以分为下面凡种情况:(l)规则集为空;(2)规则集中有一条规则;(3)规则集中有多条规则,且结论一致;(4)规则集中有多条规则,且结论不一致。

对于第(l)种情况,说明根据现有的对故障问题的认识程度,还不能够对该新的故障状态做出足够可信的故障决策:对于第(2)和第(3)种情况,只需要把结论输出即可;对于第(4)种情况,需要对所有的结论进行综合评价。假设与待诊状态相匹配的诊断决策规则共有d l,d 2,…,d r个不同的诊断结论,其中支持d i的决策规则为r l,r2,…,rm,定义d i的综合评价函数为:

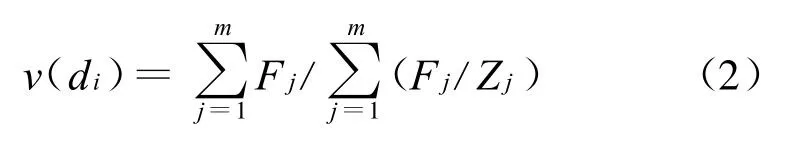
式中:F j和Z j分别为决策规则r j的覆盖度和置信度。依据上式计算出v(d1),v(d2),…,v(dr),选取综合评价函数值最大的诊断决策规则的结论作为待诊状态的最后诊断结论。

4 实例分析

本文以汽轮机振动故障诊断为例来说明上述决策网络的构造。根据运行历史数据形成的故障诊断决策表,如表1所示。

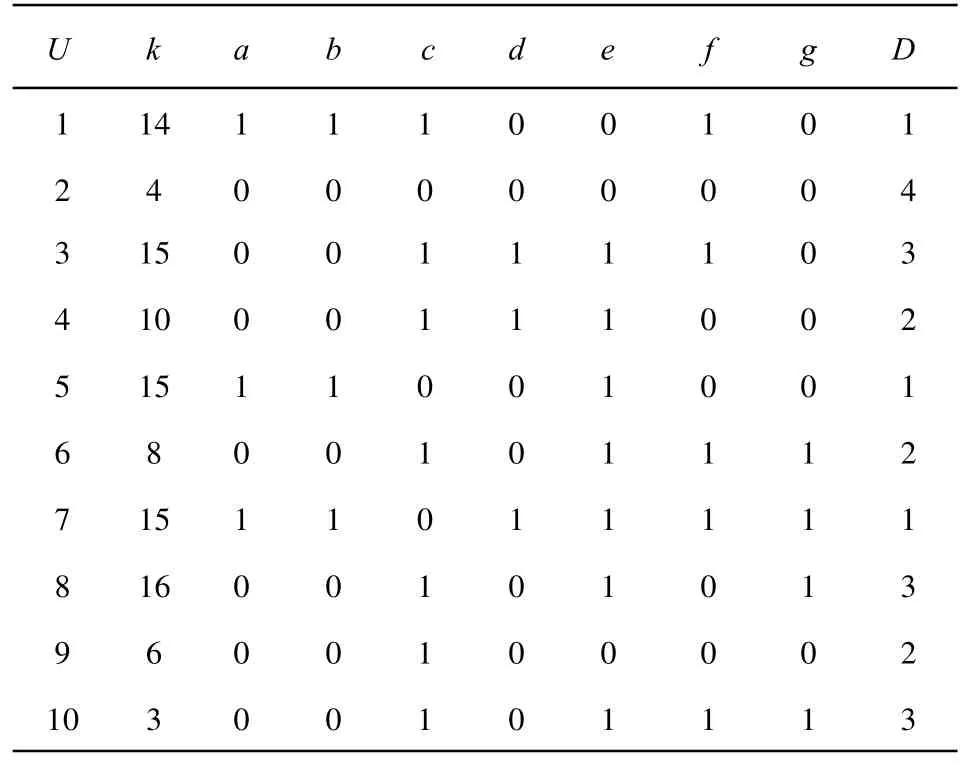
表1 故障诊断决策表

其中,U={1,2,…,10}为汽轮机振动故障的十个状态,每个故障状态的样本个数用k表示。振动信号特征频谱中的(0.3～0.44)f,(0.45～0.6)f,f,2f,3f,4f和大于4f(f为旋转频率)等7个不同频段上的幅值分量能量作为故障征兆属性。根据实践采用断点法实现连续征兆属性的离散化,故障征兆属性集 C={a,b,c,d,e,f,g},若 a,b,c∈(0.35,1)则 a,b,c取 1,否则取 0;若 d,e,f,g∈(0.20,1)则d,e,f,g取1,否则取0。决策属性集合D表示汽轮机振动故障类别:1代表油膜振荡;2代表不平衡;3代表不对中;4代表常态。

如前所述,经计算可以得到故障诊断决策系统的分辨矩阵。由分辨矩阵得到故障诊断决策系统的约简集为{{c,d,e,f},{c,d,e,g}}。从得到的两个约简出发,构造出的故障诊断网络模型如图1所示。

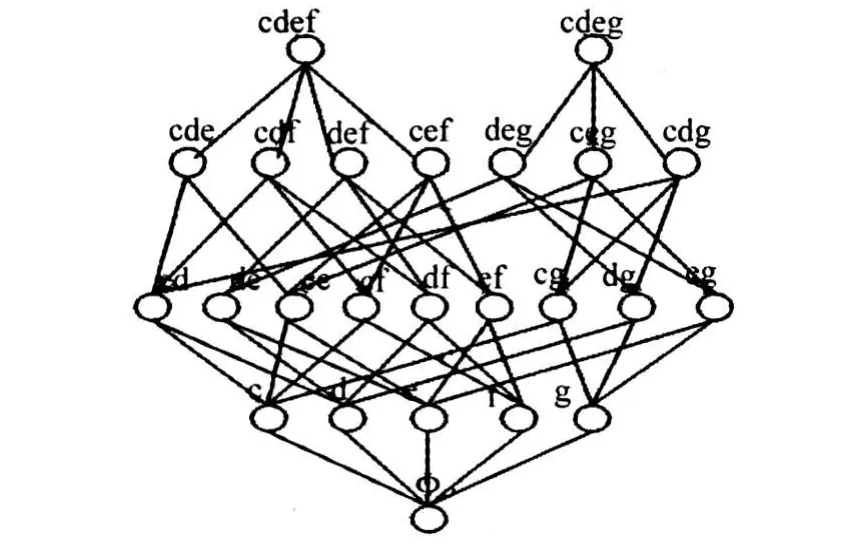
图1 故障诊断决策网络模型

从图1中可以看出,本文所构造的故障诊断决策网络由所有约简及其后继节点的全联结构成,除最下层的空节点之外,不存在没有诊断决策规则的节点,即使在诊断信息不完备的情况下,依然能够给出带有一定置信度和覆盖度的诊断决策规则。

设诊断决策规则的置信度阈值为Z0=0.8,对每个节点的决策子系统按2.2节中的步骤进行计算,将符合要求的诊断决策规则存入相应节点的规则集中。限于篇幅,本文只列出节cd f,cd,cf,d f,c上的诊断决策集合,如表2所示。

表2 节点cdf,cd,cf,d f,c上的诊断决策规则集合

从图1和表2中可以看出,利用本文所提出的方法获得的诊断决策规则简单齐整,没有重复,并且不存在某些节点诊断规则集为空的情况。

给出的实例,可以在诊断信息不完备的情况下,利用该决策网络进行故障诊断推理,在实例中汽轮机发电机组轴系系统,根据故障征兆属性c的振动信号频域特征频谱(0.35,1),可以判断征兆属性c=0。利用本文提出的方法从匹配节点c的诊断规则集可以推出诊断结果:给系统最有可能的故障类别是油膜振荡,该结论的置信度为0.88,覆盖度为0.68。实际检查结果证实了诊断的正确性。

5 结论

本文基于粗糙集理论构造的故障诊断决策网络模型,利用存储于网络中不同层次上各节点中的简洁、高效诊断决策规则集,对待诊断对象的状态给出相对满意的诊断结论。随着故障信息的增加,网络不断调整与之相匹配的规则,推理朝着置信度和覆盖度最大的诊断决策规则方向进行,其运行推理机制符合人的逻辑推理模式,体现了模型的优越性。

在实际的故障诊断应用中,由于新的故障实例的出现,新的故障征兆的获取,都将涉及到如何动态地修正现有诊断决策网络结构和动态地更新现有的诊断决策规则集的问题,这将是下一步研究的重点。

[1]YANG Ping,WU Jie,FENG Yongxin.Fuzzy fault diagnosis system for a200MW turbo-generator set[J].Automation of Electric Power Systems,2001,25(10):45-49.

[2]HUANG Wentao,ZHAO Xuezeng,WANG Weijie,et al.Rough set model for vibration fault diagnosis of steam turbine-generator set[J].Automation of Electric Power Systems,2004,28(15):80-84.

[3]GUO Qinglin,WU Huifang.A novel approach for fault diagnosis of steam turbine based on rough set data mining theory[J].Modern Electronic Technique,2006,13:074-078.

[4]PAWLAK Z.Rough Sets[J].International Journal of Information and Computer Science,1982,11(5):341-356.

[5]PAWLAK Z.Rough Sets and Intelligent Data Analysis[J].Information Sciences,2002,147(1/4):1-12.

[6]HUANG Wentao,ZHAO Xuezeng,WANG Weijie,et al.Extraction method of decision rules for fault diagnosis based on rough set theory[J].Proceedings of the CSEE,2003,11:150-155.

[7]LI Yong-min,ZHU Shan-jun,CHEN Xiang-hui,et al.Data mining model based on rough set theory[J].J Tsinghua Univ(Sci&Tech),1999,39(1):110-113.