高速公路工程设计中土方工程量计算精度的方法分析

朱洪威,谢志华

(江西理工大学环境与建筑工程学院)

高速公路工程设计中土方量计算是一项经常性的、不可或缺的工作,在整个工程量中,土方工程常占有比较大的比例。土方计算精度的高低直接影响到工程的建设工期、经济效益。因此需要进行合理化的土方调配,以便节省施工费用,加快工程进度。土方计算的目的是计算同一地块开挖(或填充)前后的挖方量(或填方量)。常见的土方计算方法有方格网法、断面法、等高线法和DEM法。

1 断面法的运用

在地形图上或碎部测量的平面图上,断面法是根据土方计算的范围,以一定的间距等分场地,将场地划分为若干个相互平行的横断面,按照设计高程与地面线所组成的断面图,计算每条横断面所围成的面积,以相邻的两断面面积的平均值乘以等分的间距,得出每相邻两断面间的体积;将各相邻断面的体积加起来,求出总体积。根据两相邻的设计断面填挖面积平均值乘以两断面的距离,就得出两相邻横断面之间的挖填土方的数量。计算公式如下

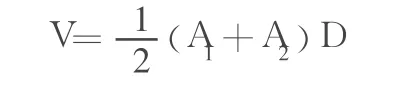
式中:A1、A2为相邻两横断面的挖方或填方面积,D为相邻两横断面之间的距离。如果同一断面既有填方又有挖方,则应分别计算。如图 1。

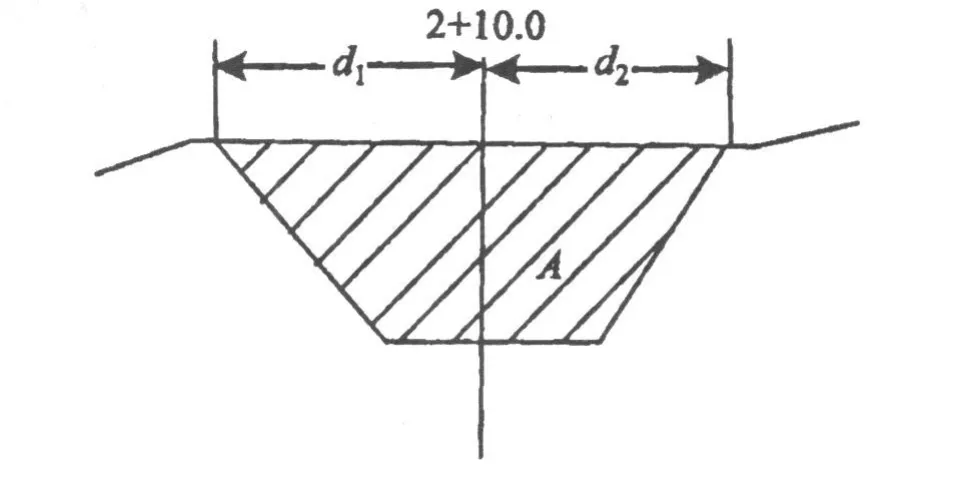
图 1 断面层

高速公路工程设计运用断面法。

方法一:根据实地测量,得出设计公路的边、角元素,可将公路建设地点绘成不规则图形,将图形分割成简单的矩形、梯形或者三角形等简单的几何图形,分别计算出面积并相加得出所需的数据。

方法二:实际勘察,搜集设计断面和横断面测量资料,然后按照一定比例绘制横断面图,最后从图上直接量算面积,进行土方石计算。

2 方格网法的运用

方格网法需要从地形图或实测得到每个方格角点的自然标高,由给出的地面设计标高,根据各点的设计标高与自然标高之差,求出零线位置,进而求出各方格的工程量,所有方格的工程量之和即为整个场地的工程量。方格网方法运用于高速公路工程设计中,计算土方工程量精度的方法很多,一般用水准测量或三角高程测量方法。测量步骤如下:

(1)在地形图上画出方格。方格的边长一般为 10m或20m(取决于地形的复杂程度和土方的估算精度)。

(2)求出各方格点的高程,并注记于右上角。

高速公路工程设计运用:

方法一:水准测量。精密水准测量必须用带测微器的精密水准仪和膨胀系数小的因瓦水准标尺,以提高读数精度、削弱温度变化对测量结果的影响;选定水准路线和埋设水准标石,用沿水准路线逐点向前推进的方式实施。

方法二:三角高程测量。该方法观测方法简单,不受地形条件限制,是测定大地控制点高程的基本方法。三角高程测量的基本原理如图,A、B为地面上两点,自A点观测 B点的竖直角为α1.2,S0为两点间水平距离,i1为 A点仪器高,i2为 B点觇标高,则 A、B两点间高差为 h1.2=S0tga1.2+i1-i2。

方法三:首先根据场地范围绘制方格网,然后根据一定范围内的各高程观测值推估方格中心O的高程值H0。

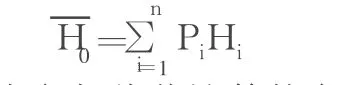
其中H1,H2,……Hn为参加估值计算的各离散点高程观测值,Pi为各点估值系数。而后进一步求得最优估值系数,进而得到最优的高程估值。

挖(填)土方量区域面积的计算时,先对判断方格网中心点是否在多边形内,如果在,那么就要计算该格网的面积,否则可以将该格网面积略去。

3 不规则三角网法

不规则三角网(TIN)是数字地面模型 DTM表现形式之一,该法利用实测地形碎部点、特征点进行三角构网,对计算区域按三棱柱法计算土方。基于不规则三角形建模是直接利用野外实测的地形特征点(离散点)构造出邻接的三角形,组成不规则三角网结构。相对于规则格网,不规则三角网具有以下优点:三角网中的点和线的分布密度和结构完全可以与地表的特征相协调,直接利用原始资料作为网格结点;不改变原始数据和精度;能够插入地性线以保存原有关键的地形特征,以及能很好地适应复杂、不规则地形,从而将地表的特征表现得淋漓尽致等。因此在利用 T1N算出的土方量时就大大提高了计算的精度。按照以下步骤:

(1)构建三角网

使用传统的 TIN生成算法之扩展法进行包括地形特征点在内的散点的初级构网。扩展法,就是指先从点集中选择一点作为起始三角形的一个端点,然后找离它距离最近的点连成一个边,以该边为基础,遵循角度最大原则或距离最小原则找到第三个点,形成初始三角形。由起始三角形的三边依次往外扩展,并进行是否重复的检测,最后将点集内所有的离散点构成三角网,直到所有建立的三角形的边都扩展过为止。在生成三角网后调用局部优化算法,使之最优。

(2)调整三角网

根据地形特征信息对初级三角网进行网形调整。第一、地性线的特点及处理方法,所谓地性线就是指能充分表达地形形状的特征线地性线不应该通过 TIN中的任何一个三角形的内部,否则三角形就会“进入”或“悬空”于地面,与实际地形不符,产生的数字地面模型(DTM)有错。当地性线与一般地形点一道参加完初级构网后,再用地形特征信息检查地性线是否成为了初级三角网的边,若是,则不再作调整;否则,作出调整。总之要务必保证TIN所表达的数字地面模型与实际地形相符。第二、地物对构网的影响及处理方法,等高线在遭遇房屋、道路等地物时需要断开,这样在地形图生成 TIN时,除了要考虑地性线的影响之外,更应该顾及到地物的影响。一般方法是:先按处理地形结构线的类似方法调整网形;然后,用“垂线法”判别闭合特征线影响区域内的三角形重心是否落在多边形内,若是,则消去该三角形(在程序中标记该三角形记录);否则保留该三角形。经测试后,去掉了所有位于地物内部之三角形,从而在特征线内形成“空白地”。第三、遭遇陡坎时,地形会发生剧烈的突变。陡坎处的地形特征表现为:在水平面上同一位置的点有两个高程且高差比较大;坎上坎下两个相邻三角形共享由两相邻陡坎点连接而成的边。当构造TIN时,只有顾及陡坎地形的影响,才能较准确的反映出实际地形。

(3)计算土方量

三角网构建好之后,用生成的三角网来计算每个三棱柱的填挖方量,最后累积得到指定范围内填方和挖方分界线。三棱柱体上表面用斜平面拟合,下表面均为水平面或参考面,计算公式为

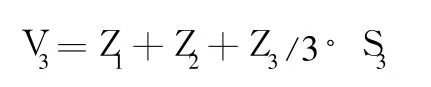
式中:Z1,Z2,Z3为三角形角点填挖高差;S3为三棱柱底面积。

可见,DTM法的精度较高,因为三角网能很好地适应复杂、不规则地形,从而更好地表达真实的地面特征。但是要注意的是 DTM方法计算土方量精度高,但其计算过程中数

据量大,占用大量存储空间。因此,如果地图本身数据量大时就应慎重考虑是否采用该方法。

4 等高线法

等高线法利用现成的绘有等高线的地形图,计算等高线的所围的面积,再根据两相邻等高线的高差,以以下公式计算土方量:

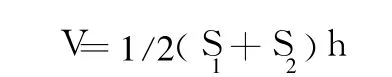
式中:S1,S2为相邻两等高线所围面积,h为相邻两等高线间的高差。

它的优点在于它能正确的表示各点的海拔高度和相邻两点的坡度,也能反映出流水侵蚀作用的方向和地貌的特征,实际应用中常和晕潼法、晕潼法、分层设色法结合使用。

5 结束语

土方量进行计算时,要考虑到地形特征、精度要求以及施工成本等方面的情况,选择合适的计算方法,达到最优的目的。由以上方法分析,断面法进行计算土方量适用于狭长地带;鉴于方格网法计算的数据量小,计算速度快,省却了DTM法庞大的数据存储量。地形起伏不大的场地适用方格网法;而地形起伏较大、精度要求高的地带则需要用到TIN的计算方法;其余的适用于等高线法。

[1] 罗德仁,邹自力,汤江龙.工程土方量计算比较分析[J].东华理工学院学报(自然科学版),2005,(1).

[2] 龚键雅.理信息系统基础[M].北京:科学出版社,2001.

[3] 王铭,宋天峰,罗阳军.均断面法计算渠道土方量的本质缺陷及改进[J].西北农林科技大学学报(自然科学版),2004,(9).

[4] 唐平英.断面法土方量计算公式的精度[J].港工技术,1998,(1).

[5] 张思亮,刘龙伟.公路涵洞、桥台反开挖土方的计算及编程[J].中外公路,2002,(1).

[6] 张婷婷,王铁良.土方量计算方法研究[J].铁道勘察,2006,(22).

[7] 欧阳平.CASS与 HTCAD的方格网法土方计算比较[J].铁道勘察,2008,(6).

[8] 张海印.土方计算精度与方格网边长之关系的研究[J].铁道勘察,2000,(1).

[9] 黄奎.基于 TIN的数字地面模型及其应用研究[D].西安建筑科技大学,2007.

[10]周越轩,刘学军,杨治洪.基于 DTM的土方工程计算与精度分析[J].长沙交通学院学报,2000,(4).

[11]姜宇涛.计算几何的不规则三角网算法研究及在 GIS中应用[D].中国地质大学(北京),2003.

[12]黎细波,马向阳,黄宗发.等高线法计算挖填土方[J].大坝与安全,2004,(z1).