冷却猪肉中假单胞菌生长预测模型的建立与验证

唐晓阳，赵 勇，孙晓红，吴启华，潘迎捷

（1.上海海洋大学食品学院，上海 201306；2.美国缅因大学食品科学与人类营养系，缅因州04469-5735）

假单胞菌通常被认为是引起冷却肉腐败的主要微生物[1-2]，因此研究假单胞菌的生长预测模型对冷却猪肉货架期和安全性的预测与监控具有重要意义。传统的微生物检测不仅耗时耗力，而且结果具有滞后性，起不到预测的作用[3]。采用数学模型预测微生物的生长可以及时有效地预报微生物的生长情况，从而预测肉品的安全性和货架期。笔者选用分离自腐败冷却猪肉的6株假单胞菌的混合培养液，研究了假单胞菌在0～10℃下的生长情况，建立生长预测模型，试图实现对0～10℃冷藏条件下假单胞菌的生长进行快速预测，为建立冷却猪肉的货架期预测模型提供一定的理论依据。

1 材料与方法

1.1 菌种

供试的假单胞菌 P1，P2，P3，P4，P5，P6 均分离自腐败猪肉，P1和P2为恶臭假单胞菌，P3和P4为荧光假单胞菌，P5和P6为莓实假单胞菌。

1.2 菌种活化

将6株菌分别从4℃保存的斜面转接至胰胨大豆胨琼脂（TSA）斜面，经30℃，24 h培养活化后，从此斜面挑取一环培养物转接至胰胨大豆胨琼脂肉汤（TSB）培养基中，放入摇床，30℃，180 r/min，培养18 h，将6种菌的培养物等比例混合，以此混合菌液为初始接种物。

1.3 菌培养物的制备

计数培养基为TSA，生长培养基为TSB，均购于上海中科昆虫生物技术开发有限公司。向每个18 cm×180 cm的试管中准确加入9.9 mL TSB培养基，121℃下灭菌20 min，备用。将上述初始接种物进行一定的梯度稀释后，按100μL的接种量接种至含有9.9 mL TSB培养基的试管中，使10 mL TSB的初始菌数大约为103～104CFU/mL。并将试管分别放于 0、2、4、7、10℃温度下培养，每隔一天取出一支试管，用平板计数法测定菌落总数[4]。

取样过程应在尽量短的时间内完成，以减少温度波动对试验结果的影响。

1.4 一级模型的拟合

一级模型的拟合运用Origin软件（Version 7.5），比较线性模型和修正的Gompertz模型拟合不同温度下假单胞菌的生长曲线，比较这两种模型的拟合效果，得出拟合效果更好的模型及其相应的一级模型参数，建立0～10℃下假单胞菌的一级模型。线性模型的表达式为：

式中Nt为微生物在时间T时的对数值（lg CFU/mL）；A为随时间无限减小时的渐进对数值（相当于初始菌数，lg CFU/mL）；k 为生长速率（h-1）。

修正的Gomperts模型[5]是双指数函数，表达式为：

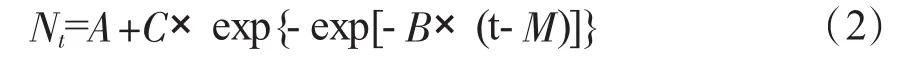
式中t为时间（h），Nt为t时的菌数，A为初始菌数N0（lg CFU/mL），C为最大菌数Nmax与初始菌数N0的差值（lg CFU/mL），B为在时间点M时的相对最大生长速率（h-1），M即是达到相对最大生长速率所需的时间（h）。由此可以得出 U（h-1）和 LPD（h）的计算公式如下：

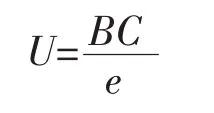
其中e=2.718 2

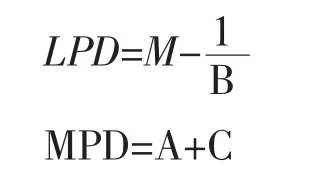
U为微生物生长的最大比生长速率（h-1），LPD为微生物生长的延滞期（h），MPD为微生物的最大细胞密度（lg CFU/mL）。

1.5 二级模型的拟合

二级模型的拟合同样运用Origin软件（Version 7.5）对实验数据进行线性回归，应用平方根模型及Arrhenius模型拟合温度-生长速率平方根曲线，研究温度对于一级模型参数的影响。

1.5.1 平方根模型拟合 平方根模型[6]是用来描述环境因子影响常用的模型，简单的表达式为：

其中aμ[（h0.5℃）-1]为U线性回归的斜率；Tmin是一个假设的概念，理论上是指微生物生长没有代谢活动时的温度（℃）。以上模型的适用范围是在[Tmin，Topt]，其中Topt是微生物生长的最适温度。将一级模型求得的U和对应的温度带入方程（3）即可得出aμ 和 Tmin。

1.5.2 Arrhenius模型拟合 Arrhenius模型[7]也是常被应用于描述温度对微生物的生长速率的影响的模型，方程式如下：

其中Aμ（h-1）为前指数因子，其作用是使模型能够拟合最大比生长速率的值；Ea为微生物生长的活化能（kJ/mol）；R 是气体常数（8.314 J/mol×K）；T为绝对温度（K）。运用Origin软件（Version 7.5）拟合实验数据，将一级模型求得的U和对应的温度带入方程（3）即可得出 Aμ和 Ea。

1.6 模型的验证

根据二级模型得出不同温度下的预测值为Upredicted，通过实验得到的数据为Uobserved，n为测定次数。计算偏差因子（bias factor）和准确因子（accuracy factor）是用来表明模型的预测值与实验实测值之间的接近程度，并以此验证所建模型的准确性。偏差因子和准确因子的表达式如下：

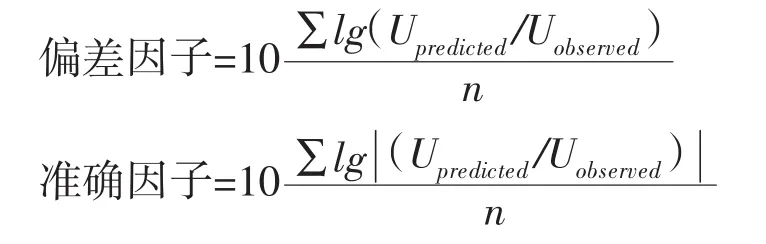
2 结果与分析

2.1 假单胞菌在不同冷藏温度下的动力学模型

采用线性模型、修正的Gompertz模型拟合0～10℃下假单胞菌的生长曲线所得统计结果如表1所示。

从多重判定系数R2来看，在0～10℃范围内，仅0℃时，线性模型的R2为0.975 0，随着温度的升高，线性模型的R2值随之下降，到10℃时仅为0.675 7，由此可见，线性模型只适合模拟低温下（如0℃，2℃）假单胞菌的生长情况，使用范围有限。而在较高的环境温度下，线性模型已不能准确地模拟假单胞菌的生长情况。修正的Gompertz模型常被用于模拟食品中微生物的生长[8-9]。从表1可以看出，在0～10℃范围内，修正的Gompertz模型的R2均在0.96以上，拟合效果良好。

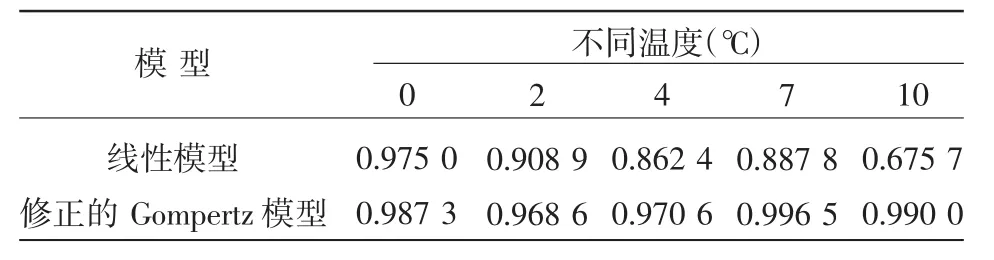
表1 假单胞菌生长曲线的统计分析R2值

图1表示的是0～10℃下修正的Gompertz对假单胞菌生长数据的拟合曲线。从图中可以看出，温度对假单胞菌的生长有明显的影响。当温度为0、2、4℃时，拟合曲线不呈典型的S型，而在7℃和10℃时，拟合曲线呈典型的S型曲线。并且0、2、4℃时的最大菌数要小于7℃和10℃时的情况，由此可推测，温度对于假单胞菌的最大菌数有一定的影响。

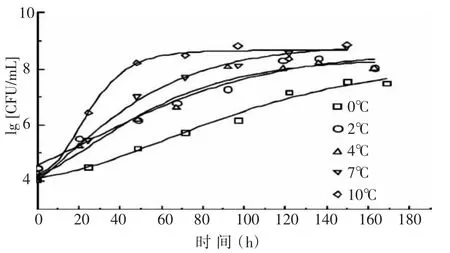
图1 假单胞菌P1在不同温度下修正的Gompertz模型拟合曲线

修正的Gompertz模型拟合假单胞菌生长曲线所得模型参数及特定生长参数如表2所示。从表2可知，随着温度的升高，假单胞菌的最大比生长速率也随之升高，当温度从0℃升高至10℃时，最大比生长速率由 0.028 4（h-1）升高到 0.126（h-1），增加了近5倍。由此可见，即使在冷藏温度下，如果超过4℃，假单胞菌的生长速率也会显著增加，从而导致食品的腐败变质加速。由此可见，在实际的生产流通过程中，环境温度一直保持在4℃以下，能更有效地延长食品的货架期，提高食品的安全性。

而温度对于微生物延滞期的影响，有相关文献表明[10]，延滞期随着温度升高而缩短。然而本文中延滞期的变化并不是很明显，可能是因为在0～10℃这个低温范围内，温度的升高对延滞期的影响不大。在2、4和7℃时延滞期出现了负值，这可能是由于生长前期的数据采集不够所致，应适当增加前期的取样次数，确保采集足够的实验数据进行建模。

由表2的模型参数值得出0～10℃下假单胞菌的一级模型分别为：

0℃时，Nt=3.878+4.398×exp{-exp[-0.017 6×（t-62.877）]}；

2℃时，Nt=3.557+5.135×exp{-exp[-0.019 6×（t-25.003）]}；

4℃时，Nt=3.438+4.946×exp{-exp[-0.026 3×（t-25.506）]}；

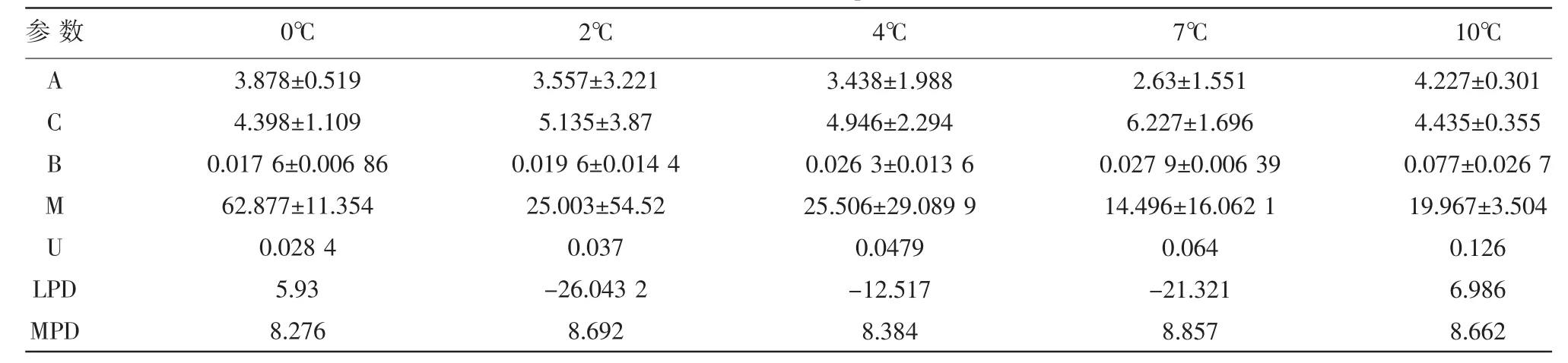
表2 假单胞菌修正的Gompertz模型参数表

7℃时，Nt=2.63+6.227×exp{-exp[-0.027 9×（t-14.496）]}；

10℃时，Nt=4.227+4.435×exp{-exp[-0.077×（t-19.967）]}。

2.2 温度对假单胞菌最大比生长速率的影响

修正的Gompertz模型能很好地预测0，2，4，7，10℃温度条件下假单胞菌的生长，但无法描述温度的变化对假单胞菌生长的影响。平方根模型和Arrhenius模型因其使用简单方便，常被用于描述温度与微生物特定动力学参数之间的关系。

2.2.1 平方根模型拟合 根据表2所示假单胞菌在0～10℃下的最大比生长速率，运用Origin软件（Version 7.5），采用线性回归拟合最大比生长速率-温度（-T），表明温度与假单胞菌的最大比生长速率呈现良好的线性关系。

2.2.2 Arrhenius模型拟合 根据表2所示假单胞菌在0～10℃下的最大比生长速率，运用软件（Version 7.5），采用线性回归拟合最大比生长速率-温度（InU-1/T），部分统计分析结果如表3所示。

从模型的方差分析来看，模型的总体显著，表明平方根模型能较好拟合0～10℃冷藏条件下假单胞菌的最大比生长速率。由图2和图3的拟合结果可知，Arrhenius模型的R2为0.971 6，高于平方根模型的R20.932 6，则选择Arrhenius模型为假单胞菌的二级预测模型。

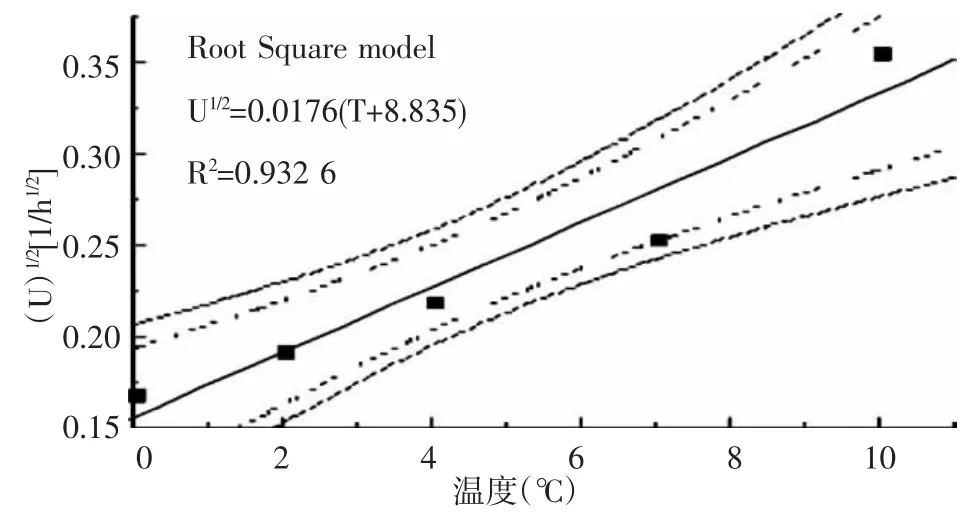
图2 假单胞菌的最大比生长速率与温度间的平方根模型及其90%和95%置信区间

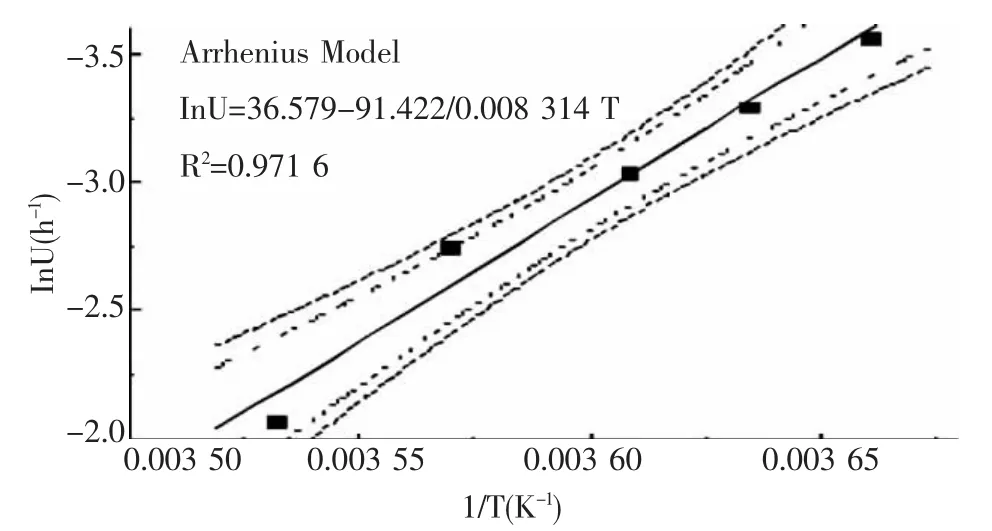
图3 假单胞菌的最大比生长速率与温度间的Arrhenius模型及其90%和95%置信区间

部分统计分析结果如表3，从模型的方差分析结果来看，模型的总体是显著的，表明Arrhenius模型能够较好地拟合不同温度下假单胞菌的最大比生长速率。绝对温度的倒数（1/T）与假单胞菌的最大比生长速率的自然对数呈良好的线性关系，lnU-1/T曲线见图3。

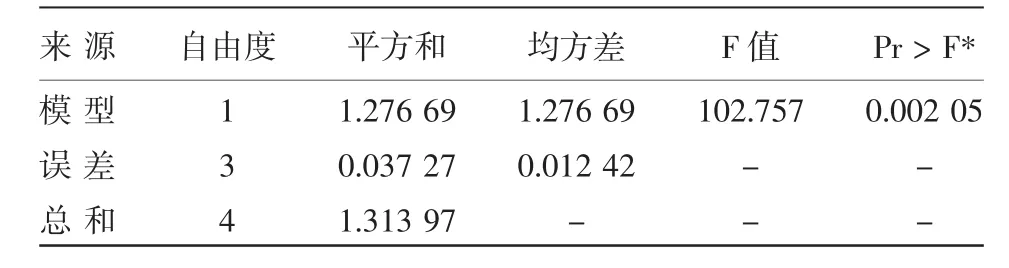
表3 假单胞菌P1的二级模型统计分析结果

从图上可以看出，二级模型的预测值都在此预测曲线的95%置信区间内，模型的预测结果可信。经过F检验，方程显著，表明此方程能较好地描述该温度范围内假单胞菌的最大比生长速率与温度之间的关系。所建二级模型如下：

InU=36.579-（91.422/0.008 314 T）），

T∈[273.15，283.15]

2.3 模型的验证

通过Origin 7.5软件求得各个温度下U的预测值（Upredicted）实测值（Uobserved），并通过计算偏差因子和准确因子来判断二级模型对最大比生长速率的预测效果。越接近于1表示模型的预测效果越好。一般认为偏差因子在0.75～1.25之间，准确因子一般在1.1～1.9之间[11]，模型即可被接受。笔者所建立的Arrhenius模型的偏差因子和准确因子分别为1.001和1.026，均接近于1，表明此模型能较好地预测0～10℃内实验室培养条件下假单胞菌的最大比生长速率。

3 结论与讨论

基于实验室的前期研究，购置于超市的冷却肉的初始菌量大多为103～104CFU/mL，选用103～104CFU/mL为液体培养基中的初始接种量。在实际中，由于样品来源不同，所经历的温度等条件不同将会导致初始菌数的不同，初始菌量不同也对食品的货架期和安全性产生影响，因此，可以进一步研究不同初始接种量下微生物的生长情况。

国内文献报道多采用平方根模型[12]建立二级模型，而没有采用其他二级模型与平方根模型进行比较。研究结果表明，Arrhenius模型的拟合效果优于平方根模型。在今后的研究中，可更多地应用Arrhenius模型来建立二级模型。

针对分离自腐败猪肉的6株假单胞菌的混合培养液进行建模，所建立的二级模型为InU=36.579-（91.422/0.008 314 T）），T∈[273.15，283.15]。然而，由于冷却猪肉中有多种不同的腐败菌和致病菌。在生产、流通、销售、贮藏各环节中，若温度控制不当，可能引起假单胞菌的大量繁殖。目前的研究主要集中于针对一株假单胞菌的生长数据来进行建模，然而实际冷却猪肉中的腐败假单胞菌主要有荧光、恶臭和莓实假单胞菌，笔者采用6株假单胞菌的混合培养物作为受试菌液，所得的生长模型更加符合实际情况，进一步为冷却猪肉的货架期预测模型的开发打下了基础。在建模过程中，如能考虑多菌种的混合培养，如假单胞菌与其他病原菌或与其他的腐败菌进行混合培养来模拟实际冷却肉品中微生物的生长情况，所建模型将更有实际意义。

常用的曲线拟合软件如SAS，Statistica，MATA LAB等软件功能强大，但需要编程，给使用者增添了一定了困难。运用Origin软件（Version7.5），对0～10℃下假单胞菌的生长数据进行拟合。Origi软件（Version 7.5）能自动生成拟合曲线，不需要编程和进行初始值的设定，使用更简便，可为模型数据库的建立提供方便。

致谢：特别感谢上海海洋大学朱雯娟、黄婧、项峰峰、成殷同学在试验上的帮助。

[1]Gill C O,Newton K G.The development of aerobic spoilage on meat stored at chill temperatures[J].Journal of Applied Bacteriology,1977,43:189-195.

[2]Newton K G,Gill C O.The development of anaerobic spoilage flora of meat stored at chill temperature [J].Journal of Applied Bacteriology,1978,44:91-95.

[3]Mcdonald K,Sun D W.Predictive food microbiology for the meat industry:a review[J].International Journal of Food Microbiology,1999,52:1-27

[4]中华人民共和国国家技术监督局，GB4789.2-2003，食品卫生微生物学检验菌落总数测定[S].北京：中国标准出版社，2004.

[5]Gibson A M,Bratchell N,Roberts T A.The effect of sodium chloride and temperature on the rate and extend of growth of Clostridium botulinum typeA in pasteurized pok slurry[J].Journal of Applied Bacteriology,1987,62:479-490.

[6]Ratkowsky D A,Olley J,McMeekin TA,et al.Relationship between temperature and growth rate of bacterial cultures[J].Journal of Bacteriology,1982,149:1-5.

[7]Koutsoumanis K,Nychas G J E.Application of a systematic experimental procedure to develop a microbial model for rapid fish shelf life predictions[J].International Journal of Food Microbiology,2000,60:171-84.

[8]Gibson A M,Bratchell N,Roberts T A.Predicting microbial growth:growth reponses of salmonellae in a laboratory medium as affected by pH,sodium chloride and storage temperature[J].International Journal of Food Microbiology,1988,6(2),155-178.

[9]McClure P J,Beaumont A L,Sutherland J P,et al.Predictive modeling of growth of Listeria monocytogenes[J].International Journal of Food Microbiology,1997,34:221-232.

[10]Augustin J C,Carlier V.Mathematical modeling the growth rate and lag time for Listeria monocytogenes[J].International Journal of Food Microbiology,2000,56:29-51.

[11]李 敏，李 耘，韩北忠.金华火腿中杂色曲霉的生长预测模型[M].食品与发酵工业，2005（11）：56-59.

[12]许 钟，肖琳琳，杨宪时.罗非鱼特定腐败菌生长动力学模型和货架期预测[J].水产学报，2005，29（4）：540-546.