基于排队网络RAID存储系统的性能评价模型
2010-07-09胡英坚
张 燕, 胡英坚, 姜 涛
(1.空军航空大学基础部,吉林长春 130022;2.长春工业大学机电工程学院,吉林长春 130012)
0 引 言
存储系统是计算机系统的重要组成部分,如何准确地预测和评价存储系统的性能,及时发现系统设计中的瓶颈和主要的性能影响因素,是提高存储系统性能的先决条件。RAID技术是一种使用非常广泛的存储技术,目前,对于这种存储系统的性能评价模型大多数是基于硬件RAID的性能分析[1],与硬件RAID控制器相比,软件RAID具有廉价、灵活性高等特点,是低端服务器存储系统的最佳解决方案,但是对软件RAID的定量分析工作很少[2]。文中针对磁盘阵列读写流程的特点,采用闭合排队网络的建模方法对软件RAID的性能进行了评价,并通过实验证明了该方法基本可以反映真实系统的性能状况。
1 排队网络的基础知识
排队网络属于排队论中的一个分支,利用排队网络模型,可以分析和评价系统的多种性能指标。
1.1 排队网络的的概念
一个排队网络是一个有向图G=(V,E),由一组顶点V={1,2,…,M}和一组边E⊆V×V组成,每个节点代表一个服务站(Service Center),服务站包括一个队列和多个服务员,E是边的集合,表示顾客流的可能通路。
一般采用节点的服务时间和节点之间的选道概率来刻画工作负载,最简单的排队网络是所有的顾客具有完全相同的性,称为单一类别排队网络。同一网络中如果存在多种不同类型的顾客,称为多类排队网络,这种情况下,每类顾客具有不同的选道行为。如果网络中的顾客数为常数,所有顾客永远循环流动,这样的排队网格称为闭合排队网络。
1.2 基本运算定律
运算定律抽象出了计算机系统多种性能间的关系,忽略系统中性能因素的随机行为,可以快速分析系统的平均性能。
little定律:

式中:N——队列系统中的平均顾客数;
X——系统的平均吞吐量;
R——系统对顾客的平均响应时间。
1)服务节点的类型为下列情况之一:
服务规则为处理器共享节点,服务由队列中所有顾客平等分享;
服务规则为先来先服务;
服务规则为后来先服务,抢占式;
无限服务员节点或者延时节点,为顾客立即提供服务,服务时间服从一定分布。
2)服务节点的服务时间为以下几种类型之一:
单服务员固定速率;
无限服务员,适用于上面提到的延时节点。
1.3 排队网络的分析方法
采用平均值法(MVA)对RAID系统进行分析,这种方法可以避免复杂的稳定状态概率。多类顾客闭合排队网络[3]的MVA分析方法如下:
假设一个闭合排队网络中有C类顾客,用向量M=(M1,M2,…,MC)表示,其中Mc代表第c(0<c<C)类顾客在网络中的个数,假设排队网络中有K个服务节点,对于每一个服务节点k,Vc,k代表第c类顾客对服务节点k的访问概率。Sc,k代表服务节点k对c类顾客的平均服务时间,则节点k对c类顾客的服务需求为:Dc,k=Vc,k*Sc,k,用X表示吞吐量(Xc代表整个系统对c类顾客的吞吐量,Xk表示节点k的吞吐量,其它符号以此类推),R代表响应时间,Q代表队列长度,则多类顾客闭合排队网络的MVA分析法基于以下3个基本公式[4-5]:
1)对于c类顾客,在节点k的平均响应时间Rc,k等于顾客排队时间和服务时间之和,对于单队列节点,表示为:
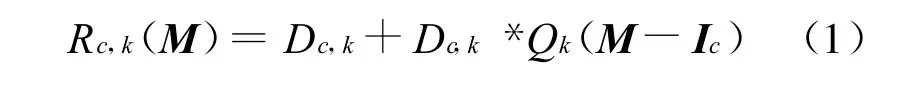
2)对于c类顾客在整个系统的吞吐量Xc(M)表示为:

3)对c类顾客,在节点k的排队长度表示为Qc,k(M)=Xc(M)*Rc,k(M),于是节点k的总的队列长度为:

式(1)~式(3)对网络中任务数形成一种递归关系,每递归一次,系统中将减少一个顾客。因此,只要给出递归初始条件,该算法即可在有限步之内计算出整个系统的吞吐量和平均响应时间。递归初始条件是显然的,对第k个节点,在系统顾客数为0时:

2 软件RAID系统的性能评价模型
用上述方法对软件RAID系统建立性能评价模型,利用评价模型对RAID系统进行分析。
2.1 模型的建立
影响软件RAID性能主要有3个部件:CPU、内存以及磁盘驱动器。CPU节点处理请求的映射以及校验计算,内存缓冲条纹数据,磁盘驱动器从内存中接收读写请求,完成实际的I/O操作,这3个部件就为模型中的服务节点。对RAID系统的读写请求抽象为顾客。请求负载采用同步方式进行读写操作,也就是说在稳定状态下当一个请求结束后,CPU会马上产生出一个类型和大小都相同的请求来代替,这样,在一段时间内,系统中的请求数是一定的。
一个RAID系统实际上就是一个多类闭合排队网络。按照读写请求的流程,软件RAID的排队网络模型如图1所示。
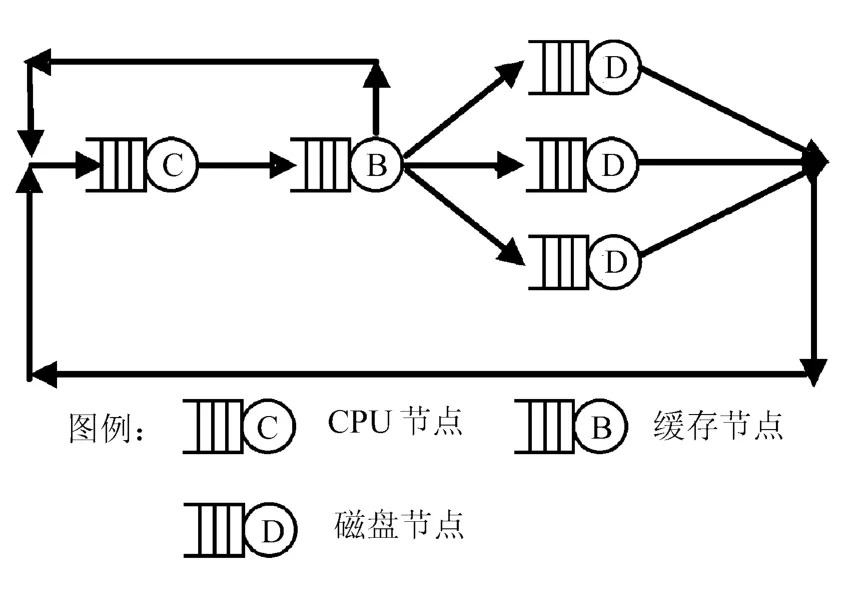
图1 软件RAID系统的排队网络模型
图中,读写请求由CPU节点发出,进入缓存节点,当请求的数据在缓存中存在时,读写命中,请求直接返回;否则,要经过RAID映射程序,将请求下发到对应的磁盘节点上。
下面以实际的RAID5系统为例,讨论其在不同负载条件下的性能。假设请求的大小为b(kB),各类节点的平均服务时间(用ST表示)的计算方式如下:
1)CPU节点:由于文中的系统完全是由软件实现的,而且所进行的实验对系统来说是一种压力实验,所以,将CPU抽象成为FCFS的排队节点,其服务时间对所有任务是一个常数。
2)缓存节点:关键的问题是缓存命中率的问题,Linux RAID的调度机制存在着条纹预读机制,缓存命中率和请求的顺序程度有关。当对RAID5的某个条纹单元进行读写操作的时候,总是会将相关的整个条纹进行预读,这样对于顺序的请求缓存命中率就比较高。文中讨论的缓存命中仅指读请求命中,对于写请求,从系统的可靠性考虑,一般采用同步写方式。预读命中的概率可以采用如下方法计算:
一次实际磁盘操作读取的数据大小Sdisk_read为请求大小Sread_req和预读大小Sread_ahead之和,表示为:

定义一个顺序度的概念,用Pseq表示。顺序度表示顺序请求在整个请求负载中所占的比率。如果请求负载是完全随机的,则顺序度为0;如果是完全顺序的请求,则顺序度为1。有了这一概念,那么一次实际的磁盘读取操作能够满足的读请求命中的个数为:

也就是说,经历Nreq_per_disk_read次读请求就需要进行一次磁盘操作,也就是缓存不命中,于是缓存不命中的概率为1/Nreq_per_disk_read,所以预读的缓存命中率为:

则缓存节点平均服务时间表示为:

3)磁盘节点:一次磁盘操作包括磁盘寻道时间、磁盘旋转时间和数据传输时间,前两者统称为定位时间。磁盘定位时间是磁盘队列长度的函数,二者的关系为:

而磁盘传输时间为数据量的线性函数表示为:
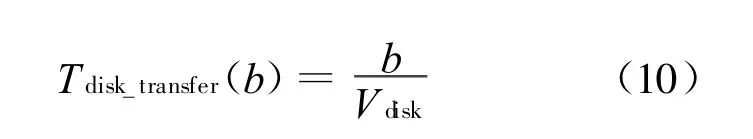
式中:b——传输数据量大小;
Vdisk——磁盘的传输速率。
为了简化计算,我们忽略磁盘的定位时间,所以:

2.2 读写请求服务的需求分析
对RAID系统的应用主要包括单用户的大数据访问和多用户的随机访问,而RAID5对大数据写和小数据写的处理方式完全不同,所以将请求负载分为读数据、大数据写和小数据写3类,它们对各节点的服务需求是不同的。
2.2.1 读和大数据写请求服务需求分析
大数据写请求是指请求的数据远远大于RAID5条纹的长度,这样在RAID层为完全条纹写的方式。这种方式和读请求的数据流程基本一致,只是有以下几点不同:
1)讨论的为同步方式,所以大数据写的缓存命中率为0。
2)大数据写增加了为计算校验单元而进行异或运算的时间,所以,CPU节点的平均响应时间要高于读操作。
3)由于RAID5的驱动程序需要生成新的校验冗余信息,所以,大数据写的实际写的数据大小为:

式中:Sreq——请求大小;
Cstripe_len——RAID5条纹长度。
以上3点在计算服务需求时表现为输入参数的不同,下面分别讨论在读(或大写)请求下各个节点服务需求计算方法。
CPU节点的服务需求表示为:

缓存节点的服务需求表示为:
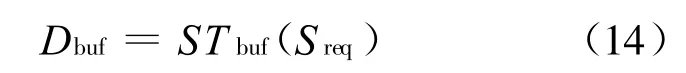
注意,此时的Sreq为实际请求大小(对于写请求进行相应的转换)。
磁盘节点的服务需求表示为:

式中:Ssub_req——每个磁盘的子请求的大小。
2.2.2 小数据写的服务需求分析
小数据写的过程是如果缓存中没有请求的条纹就读出整个条纹的数据,然后改写需要更新的条纹单元并计算校验单元,再将改写后的数据和校验单元写回到磁盘上,所以与大数据写是不同的。
对于小数据写请求,回写磁盘包含校验单元和修改后的数据单元两个数据块,所以访问概率为2/Cstripe_len,因此小写方式下磁盘服务的需求为:
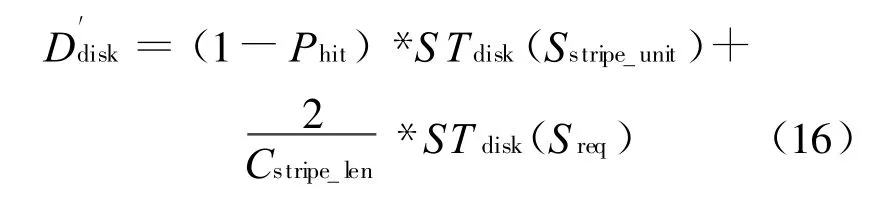
式中:Sstripe_unit——整个条纹单元的大小;
Cstripe_len——条纹长度,也就是磁盘个数。
2.3 模型分析
前面给出了RAID5在不同负载条件下的服务需求,用MVA分析方法可以计算出RAID5的吞吐量和平均响应时间。除CPU节点外,磁盘节点和缓存节点在系统任务数为m时的平均响应时间表示为:
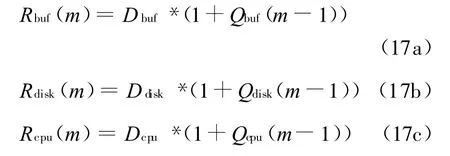
整个系统的平均响应时间为:

系统的吞吐量为:

由little定律,各节点的队列长度可计算为:
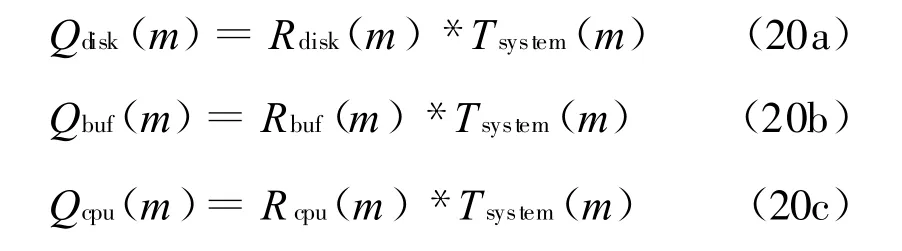
以上公式构成了递归关系,当m=1时,显然Q*(m-1)=Q*(0)=0(*代表磁盘或者缓存节点),算法即可结束。
3 实 验
通过实验比较模型的理论值和实际系统的测试值,实验参数见表1。

表1 实验参数表
测试对象为linux RAID5的磁盘阵列,实验数据分为3组,分别对应了读请求、大数据写请求和小数据写请求的理论值和实测值。
RAID5读请求性能曲线如图2所示。

图2 RAID5读请求性能曲线
RAID5大数据写请求性能曲线如图3所示。
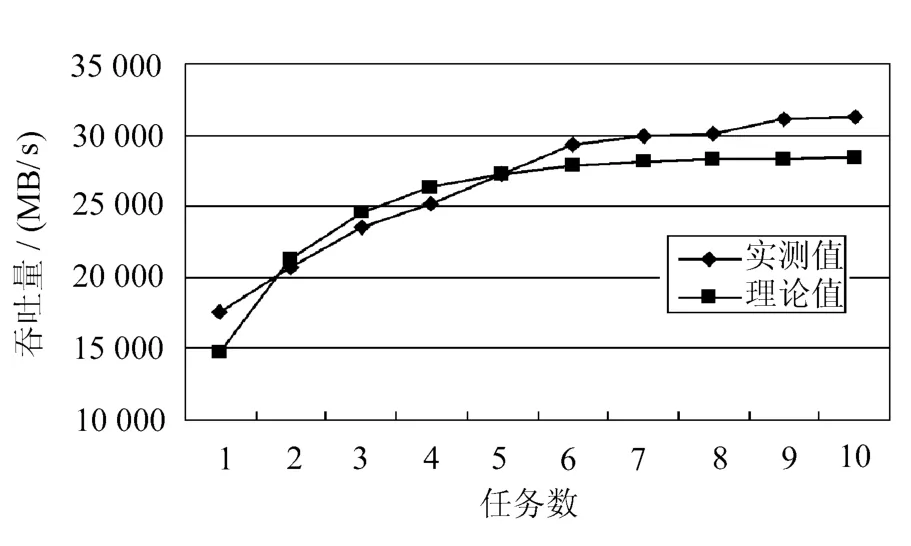
图3 RAID5大数据写请求性能曲线
RAID5小数据写请求性能曲线如图4所示。

图4 RAID5小数据写请求性能曲线
从以上3个曲线可以看出,系统的吞吐量在低负载时增加非常明显,随着负载的增加,系统中某些部件已经饱和,也就是总有任务在该节点排队等待,此时系统的吞吐量很难再增加。由于各个服务节点的服务需求是不同的,在系统负载达到极限时,整个系统的吞吐量取决于服务需求最低的那个节点,理论值同样反映了这一趋势,虽然二者有些差距,但表现是一样的。
4 结 语
通过以上的分析和实验得出,多类顾客闭合排队网络模型可以反映真实RAID系统的性能状况,采用这种模型对系统进行评价,可以在多种可行性方案中选择性价比高的设计方案;可以发现影响系统性能的瓶颈部件,提出改进方法(可以预测现有系统中那些部件的性能及提高的程度)。另外,它的工作量和费用比其它评价方法要小很多,因此,这种方法具有一定的实用性。
[1] M Uysal,G Alvarez A Merchant.A modular,analytical throughput model for modern disk arrays[C]//Proc.of the 9th Intl.Symp.on Modeling,Analysis and Simulation on Computer and Telecommunications Systems(MASCOTS),2001:183-192.
[2] Dan Feng,Hong Jiang,Yi-feng Zhu.I/O performance of an RAID10 style parallel file system[C]//Journal Computer.Sci.and Technology Nov,2004:965-972.
[3] Anand Kuratti,William H.Sanders performance analysis of RAID5 disk array[C]//Hawaii USA:Proceedings ofthe IEEE International Computer Performance and Dependability Symposium,1995:236-246.
[4] Shenze Chen,Don Towsley.A performance evalution of RAID Architectures[J].IEEE Transaction on Computers,1996,45(6):1116-1130.
[5] R Onvural.Survey of closed queueingnetworks with blocking[J].ACM Computing Surveys,1990,22(2):83-21.
[6] E Varki,A Merchant,J Xu,et al.Issues and challenges in the performance analysis of real disk arrays[J].IEEE Transactions on Parallel and Distributed Systems,2004,15(6):21-50.
[7] M Reiser,S S Lavenberg.Mean-value analysis of closed multichain queuing networks[J].Journal of the Association for Computing Machinery,1980,27(2):313-322.
[8] 谢斌,蒋宁,姜涛.某型航空发动机温度限制系统检测仪的硬件设计[J].长春工业大学报:自然科学版,2010,31(2):171-175.
