小波与神经网络结合用于电机在线监测与故障诊断

曾秀丽 ，玄兆燕，于子旺

（1. 河北理工大学 计算机与自动控制学院，唐山 063009；2. 河北理工大学 机械工程学院，唐山 063009）

0 引言

近几年来,故障诊断技术飞速发展,新的研究成果不断出现。电机作为现代工业主要的动力设备,其影响是不言而喻的。倘若电机出现故障,使企业的生产中断,将造成无可估量的经济损失。因此,针对电机在线监测与故障诊断技术的研究,具有十分重要的理论价值和实践意义。

对于大中型电机的常见故障有：运动部件的质量不平衡、运动部件配合不当、轴承磨损、转轴不对中、油膜振荡及裂纹等。这些故障最明显的特征都表现在振动信号的频率上。对于振动信号的电机状态的在线监测和故障诊断，通常采用频谱分析与相关分析的方法。然而大中型电机的故障机理较为复杂,其故障信号更多地表现为：1）信号是微弱信号，淹没于强背景中；2）信号的特征频率波动范围较大甚至出现跳动；3）信号瞬变、非平稳。因而采用频谱分析与相关分析的方法很难对故障做一个准确的诊断。大量不确定的或未知的因素可能导致：1）建立规范时存在不完全适应性；2）不能完全自动诊断，需要人工干预；3）容易出现漏检和误检等现象。

实践证明傅里叶变换的频域分析方法不能有效的提取电机振动信号中的故障信息,无法满足故障信号的特征提取要求。对此, 本文主要采用了小波与神经网络结合的思想，选取振动信号作为特征输入信号，经小波处理后，采用神经网络对相应故障进行诊断,从而建立起电机运行状态的在线监测体系，以实现对电机故障预测及诊断。

1 小波包分解的电机振动信号的特征提取

小波包是小波理论在信号处理应用上的重大发展, 它具有多维多分辨率分析的特点, 能为信号分析提供一种更为精细的方法。小波包分解是将原信号投影在不同频带上，再对这些频带内的信号进行分析即频带分析技术。小波包分析能够将频带进行多层次划分，对在多分辨率分析法中没有细分的高频部分进一步分解，从而有效提高了时频分辨率，并能根据被分析信号的特征选择相应频带, 使之与信号频谱相匹配。利用小波包分解法抽取与故障相关的特定频段, 直接利用各频段频率成分能量的变化来分析信号、提取特征。

1.1 提取特征频段

对电机振动信号W(t)进行小波包分解,提取特征频段。小波包分解可用以下递归式进行小波包分解：

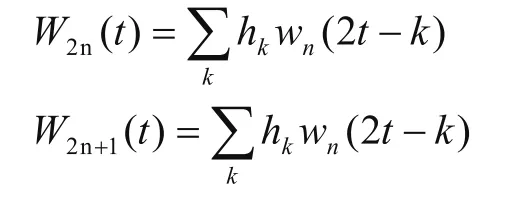
振动信号经小波包分解便可得到其在各频带内成分的特征,即低频系数和高频系数。

1.2 提取特征信号

具体做法如下:

对A/D 采样信号进行小波包分解, 分别提取最后一层从低频到高频频率成分的信号特征, 其分解过程如图1所示。图1是以3层小波包分解为例说明了小波包分解过程。

图1 小波包分解过程示意图

图1中的A表示低频轮廓信号分解, D表示高频细节信号分解,后面的数字则表示小波包分解的层数,分解具有如下关系:

S=AAA3+DAA3+ADA3+DDA3+AAD3+DAD3 +ADD3 +DDD3

由于直流电机转子出现故障时，机体振动就会受到脉冲力的作用,在靠近脉冲力作用的时刻振动信号能量较大,而在远离脉冲力作用的时刻振动信号能量相对较小，其主要成分是噪声、平稳振动信号以及低频干扰信号。因此可以利用各个频带能量的变化来提取故障特征。

其分解结构如图2 所示：

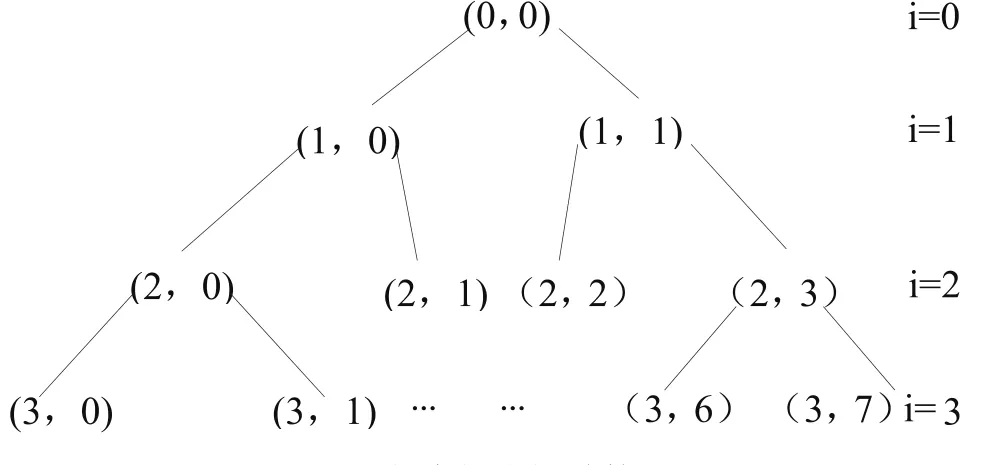
图2 小波包分解结构图

其中(0 ,0) 表示原始信号，(i ,0) 表示小波包分解的第i 层的起始结点，用( i ,φ) 表示第i 层第j 个结点，其中i = 0 ,1 ,2 ,3 , …；φ = 0 ,1 ,2 ,3 , ….若以分解为例，提取 (j=0,1,2,…,7)共8个频率成分代表的频率范围，采用下式求各频段信号能量：

式中，Xjk表示重构信号S5j的离散点的幅值。

1.3 构造特征向量

由于电机出现故障时会对各频带内的信号能量有较大的影响，因此选取能量变化突出的若干信号为特征向量，特征向量构造如下:

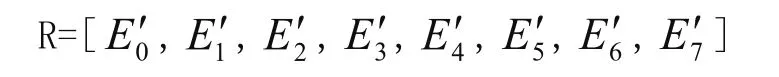
但是，当能量较大时,E'j( j = 0, 1,2, …, 7)通常是一个较大的数值，在数据分析时计算量会很大。因此，需要对特征向量进行归一化处理，则：

归一化后的特征向量为：

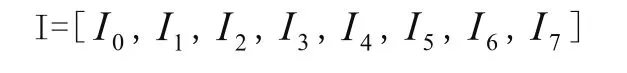
2 利用神经网络技术实现电机故障诊断

电机故障诊断的流程一般可分为状态的在线监测和故障诊断两个阶段，这两个阶段可以分以下4个步骤进行，如图3所示。

图3 电机故障诊断步骤

直流电机的故障分为电气类故障和机械类故障，其中电气类故障主要包括换向器相关故障、定子绕组相关故障和转子绕组相关故障；机械类故障主要是转子轴承故障。

经小波包分解仅获得了与故障相关的特征，还需利用神经网络进行故障的分类与识别。故障分类的神经网络常用BP 网络，但其存在一些缺陷：学习时间长，只对学习过的故障模式有识别能力，对未知未学习的模式缺乏调整手段，容易出现漏判、错判等。

自适应谐振神经网络（简称ART2）具有无监督自学习能力，对未知故障类型也具有自归类能力，从而有效的减少了漏判、错判机率。甚至可用快速算法对权值进行一步学习，因而具有以下优点：学习速度快，能对信号进行实时学习、实时处理，能对已学习模式快速响应和自动识别。这种自适应谐振神经网络有利于故障的在线监测和实时诊断。此外，它还具有一定的噪声抑制能力，可通过改变网络参数调节其噪声抑制能力；具有自归一能力, 所以对输入特征向量不必再作归一化处理。

进行故障分类及诊断的ART2 神经网络结构如图4 所示。

图4 ART2 神经网络拓扑示意

提取的特征向量I 输入F0层。输入模式中的较强部分在 中“共振”加强，较弱部分则被抑制。在F1层通过由4 个神经元zi，qi，vi，ui构成正反馈闭合回路，对输入信号进行特征向量归一化、滤波处理（增强其抗干扰能力）和非线性变换。经迭代得到稳定的中u层模式，并经ρ送入F2层，由F2层经竞争选择激活F2层故障类型，得到系统的短期记忆。F2层的输出经长期记忆Zji加权后反馈回F1层, 反馈信息与u一同送入调整子系统，检验系统长期记忆模式与输入模式的相似程度，若通过相似程度检验，则可确定输入模式属于F2层的候选模式, 并按快速学习算法, 一步完成权值的学习；若未通过检验，则强迫F2层重置并选择下一输出节点，若所有的输出节点都不能通过匹配检验，则增加一个新的输出节点即另一新类。

实际应用时将从振动信号中提取的特征向量输入ART2 网络，用学习样本（良好状态、不平衡、不对中、轴裂纹、动静碰摩、轴承磨损、运动部件配合失当、油膜振荡等运行状态所对应的振动信号中提取的特征向量）进行网络训练，得到电机正常状态及各种故障状态的长期记忆模式。用训练好的网络进行故障分类及识别，若出现未学习的故障模式，系统将自动增加一个新类。在应用时值得注意的是ρ（相似程度警戒限，为0～1之间的正数）的选择。若ρ选得太小,分类粗糙,不能把不同故障类型区分开；若ρ选得太大,分类又太细，则同一故障类型可能被划分到不同输出模式中，引起错分。ρ的选择没有一定的规则,需要在具体应用中调整。

由图4可以看出，输入向量为I=[I0,I1,I2,…IN-1]，系统的输出是一个M维的向量Y=[Y0,Y1,Y2,…YN-1]。用学习样本进行网络训练时，依次送入向量I (K),K =0,1,2,3…,其中K为特征向量送入神经网络的时序编号,每送进一个向量I(K)，就可以计算出输出向量Y(K)，从而实现了对电机故障的分类及识别。

利用小波包分析方法分析故障信号,再进一步的利用神经网络的学习训练功能进行电机的在线监测与状态诊断. 目前，已有相关实验证明了该方法的正确性和有效性,可以扩展应用到电机综合故障诊断系统研究与应用之中。

3 结论

1）利用小波包分解技术,可准确提取出故障特征频率,进而有效监测电机工作状态,避免了采用频谱分析与相关分析方法进行故障诊断时的不足。

2）利用ART2自适应谐振神经网络进行电机故障的分类及诊断,以减少漏判、错判的机率。

3）基于小波与神经网络相结合的思想，能对特征输入信号进行实时学习、实时处理, 能对已学习模式快速响应和自动识别，避免了BP网络学习时间长等缺陷，这有利于在线监测和故障诊断，符合对大中型电机远程状态进行在线监测和故障诊断的要求。

[1] 朱启兵.基于小波理论的非平稳信号特征提取与智能诊断方法研究[D].沈阳:东北大学,2005.

[2] 袁曾任.人工神经元网络及其应用[M].北京:清华大学出版社,1999.

[3] 熊富强,张航.基于小波-神经网络的汽轮机转子故障诊断[J].控制理论与应用,2007,26(12):123.

[4] 刘冬生,赵辉,王红君,岳有军.基于小波分析和神经网络的电机故障诊断方法研究[J].天津理工大学学报,2009,25(1):11-14.

[5] Carpenter GA,Grossberg S,Rosen DB.ART2-A :an adaptive resonance algorithm for rapid category learning and recognition[J].Neural Network,1991,2(4):151-156.

[6] Carpenter GA,Grossberg S.ART2:self-organization of stable category recognition codes for analog input patterns[J].Applied Optics,1987,26 (23):4919-4930.