基于二次误差测度的车身网格简化算法研究

李 旭， 周 卓， 时艳茹， 尹鹏举

（山东理工大学交通与车辆工程学院，山东 淄博 255049）

近年来，逆向工程在企业的新车型设计中得到了广泛的应用。由于ATOS等非接触式扫描设备的出现，人们很容易获取大量点云数据，三角化以后具有数百万的三角网格，数据如此庞大而计算机工具本身计算能力的限制使得车身模型构建较慢而且效率低下[1]。寻求一种能够减少三角网格数量而尽量不损失原模型拓扑形状的简化算法对车身曲面重构具有重要的意义。

目前对网格简化的主要方法有删减法和顶点聚类算法。删减法[2,6]通过重复依次删除对模型特征影响较小的几何元素并重新三角化来达到简化模型的目的；根据删除的几何元素的不同，通常又可以分成顶点删除法、边折叠法和三角面片折叠法等。删减法具有编码简单和运行速度快的特点，但在需要保持拓扑关系的应用中简化效率会受到一定的影响。顶点聚类算法[3]根据一定的规则，将原始网格模型中的两个或多个顶点合并成一个顶点，并删除合并顶点后的退化三角形，从而到达简化网格面片数量，实现网格模型的简化的目的。顶点聚类法能处理任意拓扑类型的网格模型，算法简单，速度较快。但由于简化误差控制困难，容易丢失较小结构的细节，因此通常简化模型的质量不高。

本文对基于二次误差测度的边折叠简化算法进行了研究，综合考虑了车身逆向工程对网格简化的精确性与快速性的要求，使之保留了车身曲面中边界，孔洞和棱线等特征，并通过合理的数据结构的构建提高了算法简化的速度。本文对某轿车测量点云局部区域进行了简化和分析，并与三维造型软件imageware中简化效果进行了比较，结果表明，基于二次测度算法不仅更快速，而且可达到更好的简化效果，很适合于海量车身拓扑网格的简化。

1 二次误差测度边折叠简化算法

1.1 边折叠简化算法[4-5]

（1）将顶点vi移到位置；

（2）将出现vj的所有地方用vi代替，即将所有关联至vj的边关联至vi；

（3）删除vj，删除所有的退化边和退化三

边折叠简化算法的基本思想是：在每一次简化操作中以边作为被删除的基本几何元素，并增加一个新点，所有与被删除边相连的点都与该新点相连，使模型仍保持是三角形网格。在进行多次的选择性边折叠后，模型就可简化到任何程度。角形（图中灰色三角片）。

如图1所示，每折叠一条非边界边，模型减少2个三角形，1个顶点，3条边；折叠一条边界边，模型减少1个三角形，1个顶点，2条边。边折叠简化模型网格必须与原网格尽量相似，这取决于边折叠的顺序和边折叠后生成的新顶点的位置。

图1 边折叠示意图

1.2 二次误差测度

如何选择合适的边进行收缩及如何生成新的顶点，有一个选择误差测度标准的问题。本文采用二次误差测度准则。

二次误差测度最早由Garland提出，该方法将点到相关平面的距离的平方和作为误差测度。它的优点是具有极高的计算速度，较小的内存消耗，而且得到的简化网格具有较高的质量。虽然该方法不是全局优化的，但得到的简化网格的质量可以和全局优化方法相媲美。

设对边(vi, vj)进行折叠，则与边(vi, vj)相关联的三角形集合 Planes(i, j)构成了原模型上的一个区域。设边折叠后生成的新位置v为[x, y, z,1]T，定义这次边折叠带来的新误差Δ ()为到三角形集合Planes(i, j)中每个三角形所在面的距离的平方和，即

其中 p =[a, b, c, d ]T表示三角形集合Planes(i, j)中的每个三角形所在面的平面方程ax + b y + c z + d =0 ，且有 a2+b2+c2=1。式(1)可变换如下

其中 Kp是4×4的对称矩阵，称为三角形的误差矩阵，它的定义如下

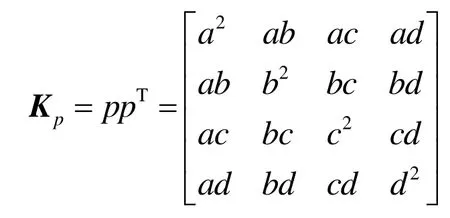
Q称为本次边折叠的误差矩阵，定义如下

算法中为了快速、简单地计算边收缩的误差，首先，将Planes(i)中的所有三角形的误差矩阵求和，得到了关于顶点vi的误差矩阵Qi，同样可以得到顶点vj的误差矩阵Qj；然后，将顶点vi和顶点vj的误差矩阵Qi、Qj相加，近似成该边折叠的误差矩阵Q，即Q=Qi+Qj；最后求出边折叠的误差Δ)=TQ，则新顶点v的误差矩阵为Q。

2 算法的实现

2.1 数据结构

（1）顶点信息

采用数组表示顶点信息列表。顶点列表除了记录每个顶点的坐标位置，还记录了每个顶点的误差矩阵，顶点相关的面，顶点相关的顶点。由于每个顶点关联面的个数不定，所以关联面采用动态链表来表示。

（2）三角面信息

三角面片信息表记录了模型中三角面片的构成信息、状态信息。构成信息包括了三角形三个顶点的序号，并且要保证这3个顶点是按逆时针排列。在简化过程中，由于算法要对边进行折叠，一些三角形会发生变形，退化成点或线段，在以后的简化阶段和模型绘制阶段将不对这些三角形进行处理，因此设置一个标志字段记录三角形面片中各顶点的状态，只有当3个顶点均未褪化时，能够连接为三角形，可以继续处理。三角形面片信息也采用数组表示。

（3）比较误差测度的堆

折叠误差堆的排序采用最小堆排序。该最小堆以边折叠误差值作为关键字。堆是逻辑上具有完全二叉树形式的数组，数组中每个元素除了记录折叠误差外，还记录了每条边折叠后的新位置，边关联的两个顶点的序号。

2.2 算法流程图

基于二次测度的简化算法主要步骤包括：判断各边是否为边界边，如果为边界边，要作出与此边垂直并包含此边的辅助面计算每个三角形和辅助面的误差矩阵，并将各个顶点关联的三角形或辅助面误差矩阵求加和，得到该顶点误差矩阵；对折叠误差堆进行排序；进行边折叠；更新简化图形；如果网格数目达到简化要求，则结束压缩。基于二次误差测度的简化算法详细流程图如图2所示。

3 在车身逆向工程中的应用算例

本文使用 VC++6.0编程实现了基于二次误差测度的简化算法，并通过opengl应用接口实现了曲面或实体模型的显示。图3是编程所实现的用户界面，可以进行文件的读入，图形的简化，放大缩小，旋转等交互处理。以及便于保存简化后，符合用户需求的图形文件，可同时保存为obj文本格式和 stl格式，该文件格式可以导入Imageware和UG中进行后续处理，这样也为以此两个软件为主的逆向工程提供了大大的方便。

图2 算法流程图

如图4为某轿车发动机罩初始模型及本文算法与imageware中简化算法对其简化的结果。可以看到，本算法在1.2秒的时间之内将6万个点简化成 5000个三角形，如图4(b)所示，通过局部放大可以看到，简化模型的边界与初始模型的边界是基本相同的，而过渡处的棱线处仍然保持了原有的特征，而在图4(c)中， imageware使用了3秒钟将同一模型简化成5000个三角形，同样经过局部放大，可以看到所生成的网格边界参差不齐与初始网格的边界已经完全不同，棱线特征基本已经消失。由此比较可见，imageware中简化速度慢，而且丢失了大量重要的信息，效果很差。基于二次误差的简化方法能够快速实现网格的简化，且很好的保持了原始网格的重要特征。

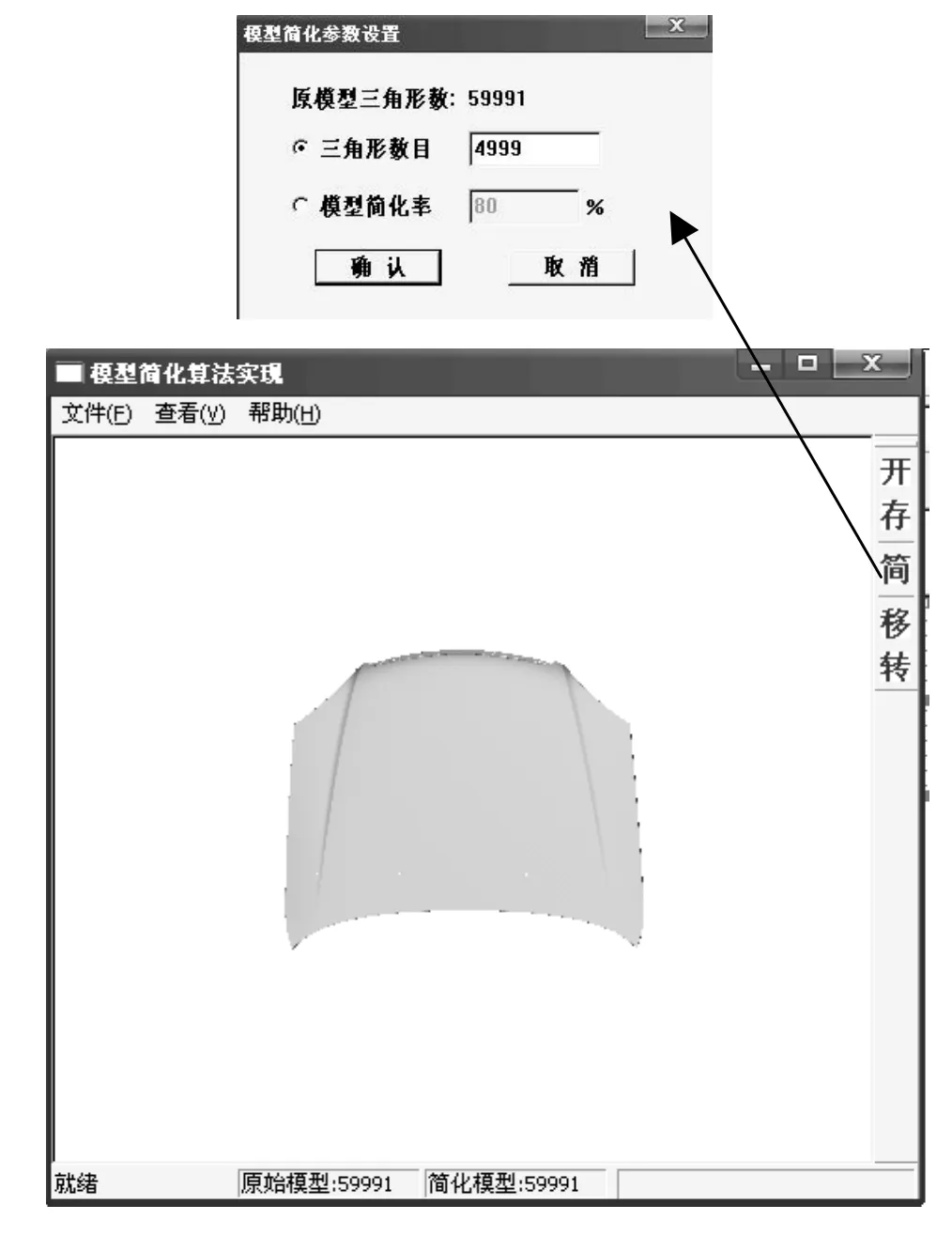
图3 图形显示界面

4 结束语

从实验结果来看，本文采用的二次误差测度边压缩简化算法比imageware三角形压缩算法计算速度快而且能够更好的保持初始网格特征信息，逆向工程对点云的处理阶段即要求能够尽可能的减少点云的数量以加快运算速度而且要尽可能的保持点云信息，本算法快速而精确很适合应用于车身曲面的逆向工程。

图4 对轿车发动机罩点云的简化

[1]王建勇, 贺 炜, 刘言松. 逆向工程技术及其实物反求应用[J]. 机床与液压, 2005, (5): 34-36.

[2]Schroder W, Zarge J, Lorensen W. Decimation of triangle meshes [J]. Computer Graphics, 1992, 26(2):65-70.

[3]Low K-L, Tan T-S. Model simplification using vertex-clustering [C]//Proceedings of the 1997 Symposium on Interactive 3D Graphics, ACM SIGGRAPH’97, 1997: 156-163.

[4]Garland M. Simplification using quadric error metrics [J].Computer Graphics, 1997, 31(3): 209-216.

[5]Hoppe H. Progressive meshes [J]. Computer Graphics,1996, 30(1): 99-108.

[6]周 昆, 潘志庚, 石教英. 基于三角形折叠的网格简化算法[J]. 计算机学报, 1998, 21(6): 506-513.