一种循环冗余校验码的设计及VHDL语言实现

尹晓琦

(淮阴工学院，江苏 淮安 223003)

0 引言

数据通信技术是计算机网络技术发展的基础，已经成为现代生活中必不可少的一部分。但通过通信信道传输的数据往往会有差错的产生，而且差错的产生是不可避免的，我们所关心的是分析差错产生的原因与差错类型，研究检查是否出现差错及如何纠正差错。循环冗余码(CRC)是一种在数据通信和数据压缩中广泛采用的差错控制编码。循环冗余校验CRC即Cyclic Redundancy Check，是一种数字通信中的信道编码技术。CRC码在通讯传输中的应用范围十分广泛，如USB协议、IEEE802.3标准、IEEE802.11标准、RFID协议等都采用了CRC作为正确性校验的方法。

1 CRC码的基本原理

经过CRC方式编码的串行发送序列码，可称为CRC码，共由两部分构成:k位有效信息数据和r位CRC校验码，如图1所示。

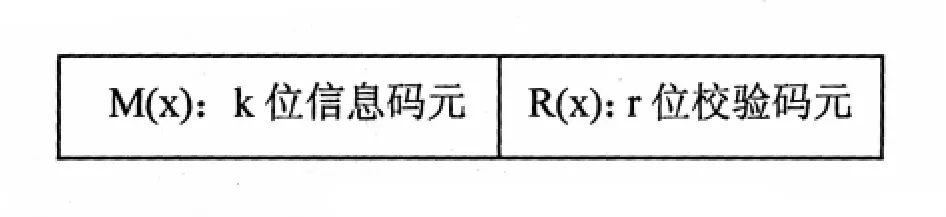
图1 CRC码结构图

其中，r位CRC校验码是通过k位有效信息序列被一个事先选择的r+1位“生成多项式”相除后得到的(r位余数即是CRC校验码)，这里的除法是“模2运算”。CRC校验码一般在有效信息发送时产生，加在有效信息后被发送;在接收端，CRC码用同样的生成多项式相除，除尽表示无误，弃掉r位CRC校验码，接收有效信息;反之，则表示传输出错，纠错或请求重发。

CRC码的生成多项式的次数r就是校验位的个数，信息分组的比特数k并无特别限制。CRC码的编码效率是，一般也是用来描述CRC码的效率。通常，较长的信息分组使用较长的CRC生成多项式。

CRC码的编码结果有2k种，他们都是g(x)的倍数。信道中可能发生的非全0错误图样共有2n－1=2k+r－1种。当错误图样能被g(x)整除，也即错误图样本身是一个码字时，这样的错误将不会被接收器发现，使译码器报告无错，称此情况为发生漏检。不同的错误图样的个数有2n=2k+r个，其中能被g(x)整除的错误图样的个数是2k个，除去一个全0错误图样表示无错外，其余的错误图样都能导致漏检，这些错误图样的个数是2k－1个，占总错误图样的比例为2k－1/2k+r≈2－r。例如:CRC－16不能检出的错误图样只占总可能错误图样的1/216，约为六万分之一。在许多应用中，出错本身是小概率事件，出错时错误图样恰好是g(x)的倍数的概率更小。因而，CRC码是一个强有力的检错码。CRC码位数越长，则检错能力也越强。

2 CRC码的实现方法

实际应用的过程一般是在发送端计算发送信息的CRC码值，并将它作为信息包/帧的一部分传递给接收端;接收端将对接收到的信息进行 CRC码计算，并与发送过来的CRC码进行比较，从而判断接收的信息是否正确。CRC码的计算实现可以有多种方法，它可以通过软件方式计算，也可以通过硬件方式计算，还可以通过查表得到。发送时，CRC码的计算过程可以在传输之前完成，也可以在传输过程中进行;对CRC码的校验可以在接收的同时进行，也可以在传输完成之后进行。

CRC码的计算可以是按位串行进行的，也可以是多位并行进行的。CRC码的产生与检查可以有两种方式:计算法和查表法。对于硬件实现来说，查表法没有太大的优势，因为它要占用很多芯片面积来构造一个ROM实现的表。实际硬件设计中，CRC码的计算可以有两种方式，一种是串行方式，另一种是并行方式。串行方式就是按位产生CRC码，也就是通过一个线性反馈移位寄存器(LFSR)按每次输入一位的方式来产生CRC码。这种方式结构规则，但每个时钟周期只能计算1位的结果，速度较慢。并行方式是每次输入一组并行数据，同时产生出CRC码结果，并行方式处理速度较快。在CRC码检查时也可以有两种方式，一种是对要检查的部分采用与CRC码产生同样的方法计算CRC码的值，然后看是否与传输过来的CRC码相同;另一种是对接收的所有部分(包括CRC码)计算新的CRC码值，看是否得到预计的结果(余数)。

2.1 CRC生成多项式

在串行数据传输中广泛采用循环冗余校验码来测试一个数据包是否有错误发生，虽然循环冗余校验码的理论较为复杂，但实现检错的基本原理十分简单。在m位信息码后再拼接r位的校验码，整个编码长度为n位，因此这种编码又叫(n，k)码。对于一个给定的(n，k)码，可以证明存在一个最高次幂为n－k=r的多项式g(x)。根据g(x)可以生成k位信息的校验码，而g(x)叫做这个码的生成多项式。CRC检错码的检错能力与其生成多项式g(x)密切相关。(n，k)循环码的生成多项式g(x)的一般形式为:

g(x)的首项系数为1，末项系数也必须为1;g(x)的次数越高，其检错能力越强。

2.2 CRC码的生成及校验

校验码的具体生成过程为:假设发送信息用数据多项式m(x)表示，将m(x)左移n－k位，则可表示成m(x)×xn－k，这样m(x)的右边就会空出n－k位，即校验码的位置，通过 m(x)×xn－k除以生成多项式g(x)得到的商Q(x)和余数r(x)，其中余数r(x)就是校验码，即:

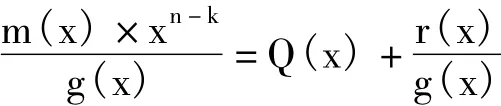
在发送端发送数据时余数加到信息码之后一同发出，将一组信息码和余数组成的数据块称为一个码元，设为T(x)，则有

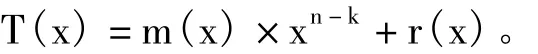
在接收端任一组多项式T(x)都应被生成多项式g(x)整除，如果传输中未发生错误，则接收码元与发送码元相同，故接收的码元必定能被g(x)整除;若码元在传输中发生错误，则接收的码元可能除不尽而有余数，因此我们就以余数是否为零来判断接收码元中有无错误。可能有错误的码元正好也被g(x)整除，这时校验无效，但通过选择多项式g(x)和增加冗余位数，使余数r(x)多项式的位数增多，来降低发生这种错误的概率。生成多项式应该能满足当任何一位发生传送错误时都能使余数不为0，并且不同位发生错误时应该使余数也不同，这样不但能校验错误，而且能推断是哪一位出错，从而有利于准确地纠错。另外，CRC是一种(n，k)循环码，能够检测出如下错误:

(1)突发长度l≤n－k的突发错误;

(2)大部分突发长度l=n－k+1的错误(不可检测到的这类错误只占2－(n－k－1));

(3)大部分突发长度l＞n－k+1的错误(不可检测到的这类错误只占2－(n－k));

(4)所有与准用码组的距离小于dmin的错误;

(5)所有奇数个随机错误。

3 循环冗余校验CRC码的设计

3.1 CRC校验生成模块

所设计的16位CRC发生器和校验器，完成12位数据附加5位CRC校验码发送和接收，系统由2个模块组成:CRC校验生成模块(发送)和CRC校验检错模块(接收)，输入、输出都采用并行的CRC校验生成方式。

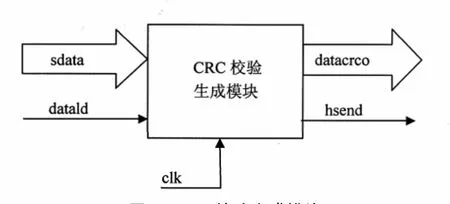
图2 CRC校验生成模块

sdata:12位的待发送信息;

datald:sdata的装载信息;

clk:时钟信号;

datacrco:附加上5位 CRC校验码的17位CRC码，在生成模块被发送;

hsend:生成、检错模块的握手信号，协调相互之间关系。

3.2 CRC校验检错模块

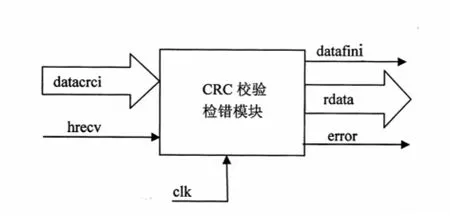
图3 CRC校验检错模块

datacrci:附加上5位CRC校验码的17位CRC码，在检错模块被接收;

hrecv:生成、检错模块的握手信号，协调相互之间关系;

clk:时钟信号;

datafini:数据接收校验完成;

rdata:检错模块接收的12位有效信息数据;

error:误码警告信号。

4 VHDL语言实现与仿真结果

本次设计的CRC编码器和解码器，利用MAX+plusII软件平台，根据CRC编码原理，采用硬件描述语言VHDL文本输入法。为了提高编码的速度，在设计时采用信息位并行输入，CRC码并行输出的算法。生成多项式为G(x)=x5+x4+x2+1，校验位为5位，有效信息位为12位，最终生成17位CRC码。部分程序代码如下:

CRC生成和校验模块的仿真结果如图4所示。从图4中可以看出，信息码m(x)为B5D(H)，即 101101011101，生成多项式为 35(H)，即110101。

如果用竖式除法，用去除以，得:

余数 r(x)=x3+x，即1010，就是 CRC校验码，把它加到信息码101101011101后面就生成了CRC 码为 10110101110101010，既 16BAA(H)，这个码可以被35(H)除尽，说明仿真波形中的编码和校验结果是正确的。

图4 CRC码的仿真波形图

5 结束语

循环冗余校验CRC(CyclicRedundancyCheck)码是由分组线性码的分支而来，其主要应用是二元码组。编码和解码方法简单，检错和纠错能力强且误判概率很低，在通信领域广泛用于实现差错控制。本文设计的以EDA设计工具MAX+PLUSII软件为基础，利用VHDL语言设计的CRC(17，12)编、解码器，具有编码速度快，可靠性高以及易于大规模集成等优点。

［1］陆正福，官金兰，吴立芝.CRC码的Simulink仿真实验［J］.实验科学与技术，2007，5(5):45－48.

［2］唐鹏程，邹久朋.CRC校验码在单片机中的程序实现及其冗余码表的求取［J］.工业仪表与自动化装置，2004，(3):55－57.

［3］李宥谋，房鼎益.CRC编码算法研究与实现［J］.西北大学学报:自然科学版，2006，36(6):895－898.

［4］叶懋，刘宇红，刘桥.CRC码的FPGA实现［J］.重庆工学院学报，2008，21(5):85－87.

［5］黄熙.一种快速循环冗余校验算法的Verilog实现［J］.福建电脑，2009，(11):79－80.

［6］徐光辉，程东旭.基于 FPGA的嵌入式开发与应用［M］.北京:电子工业出版社，2006.

［7］陈荣，陈华.VHDL芯片设计［M］.北京:机械工业出版社，2006.

［8］樊昌信.通信原理［M］.北京:国防工业出版社，2006.